Link zu einem Monochordbausatz-Angebot mit sehr guter Klangqualität
Tutorials zur Musiktheorie
Mathe Vital der TU München: Mathematik und Musik

13-saitiges Monochord (eingestellt ist eine chromatische, gleichförmig gestimmte Skala)
Bausatzquelle (Original 20-saitig) .
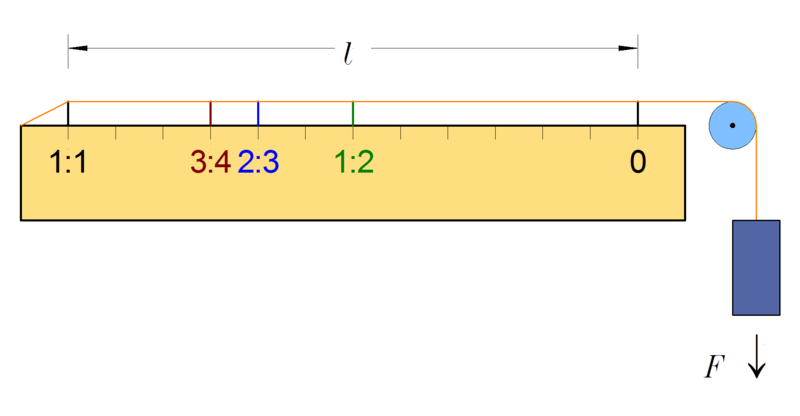
Einfache Zahlverhältnisse am Monochord (Quelle hier)
Grundlage: Halbierung der Grundsaite lässt die Oktave zum Grundton erklingen; zur Oktave gehört also das Saitenlängenverhältnis 1:2.
Zur reinen Quinte gehört das Verhältnis 2:3, zur Quarte das Verhältnis 3:4.
Die Schwingungsfrequenz des Tones ist umgekehrt proportional zur Saitenlänge. Die Saite, die um 1 Oktave höher klingt als die Grundsaite, hat die doppelte Schwingungsfrequenz: Frequenzverhältnis 2:1. Zur Quinte gehört demnach das Frequenzverhältnis 3:2, zur Quarte das Frequenzverhältnis 4:3.
Erzeugen neuer Tonleitertöne via Quinten (⋅3/2) und Reoktavierungen (⋅1/2) |
| Ein Chor, der diese Intervallfolge sänge (und zwar in reinen Quinten und reinen Oktaven), wäre nach einmaligem Durchsingen dieser Folge etwas "gestiegen". Sänge er diese Intervallfolge vier Mal hintereinander, wäre er fast einen Halbton angestiegen. Beim Singen in einem Tonsystem mit reinen Quinten und reinen Oktaven, kann also der Grundton (die Tonika) nicht konstant gehalten werden. Die Tonika verändert sich je nach Melodiefolge. Bei mehrstimmigem Gesang entstünde mit der Zeit eine völlige Verstimmung der einzelnen Stimmen gegeneinander. |
Seit der Antike versuchte man nun, ausgehend von diesen Grundintervallen ein Tonleitersystem aufzubauen, das sich nach einer Oktave wiederholt. Dabei tritt folgende grundlegende Schwierigkeit auf:
Es gibt kein Tonsystem, das auf lauter reinen Quinten (3 : 2) aufgebaut ist und welches zugleich oktavenperiodisch ist.
Der Grund dafür ist einfach: Wir starten mit einem Grundton, z.B. c. Dieser habe die Frequenz 1f. Nun erzeugen wir die Quinte dazu (g). Dazu multiplizieren wir die Frequenz f mit dem Bruch 3/2. Zu dieser Quinte erzeugen wir erneut die Quinte: erneute Multiplikation mit 3/2, also insgesamt Multiplikation von f mit (3/2)2 . Damit haben wir jedoch bereits die erste Oktave überschritten. Wir re-oktavieren deshalb diesen neuen Ton (d'), indem wir seine Frequenz halbieren (mit 1/2 multiplizieren). Nun haben wir einen Ton (d) innerhalb der ersten Oktave gewonnen. So fahren wir weiter und erzeugen laufend neue Quinten, die wir bei Bedarf in die erste Oktave re-oktavieren. Wir behaupten: Dieses Verfahren hört nie auf, d.h. es entstehen unbegrenzt viele neue Töne. Wir erhalten nie ein Tonleitersystem mit einer endlichen Anzahl von Tönen.
Beweis: Das Verfahren würde aufhören, wenn wir irgendwann (nach dem Erzeugen von x neuen Quinten und y Reoktavierungen) wieder beim Startton mit Grundfrequenz 1⋅f landeten. Dies würde bedeuten:
(3/2)x⋅ (1/2)y = 1 oder 3x = 2x+y. Dies ist jedoch mit ganzzahligen x und y unmöglich, denn eine reine Dreierpotenz (links) kann nicht zugleich eine reine Zweierpotenz (rechts) sein. Also wird unser Vorgehen via reine Quinten und Reoktavierung unbegrenzt neue Töne erzeugen. Wir erhalten keine Tonleiter mit einer endlichen Anzahl von Tönen.
Diese mathematisch erzwungene Abkehr vom Ideal reiner Quintensysteme führte nun im Laufe der Musikgeschichte zu den verschiedensten Varianten von Tonsystemen.
Schwingungen einer Stimmgabel

Zum Applet
Die Zinken einer Stimmgabel schwingen nahezu harmonisch. Befestigt man an einer Zinke einen Stahlstift und lässt die Gabel über eine berusste Glasplatte laufen, entsteht eine Zeitdarstellung der Auslenkungen. Das Geogebramodell imitiert diesen Vorgang in Zeitlupe. Es entsteht das Bild einer Sinusfunktion.
Gegeben ist eine Menge von Tönen: T = {..., c, d, e, f, ...} (der "Tonvorrat" unseres Musiksystems).
Sei x ein Ton ∈ T mit Frequenz fx und y ein Ton ∈ T mit Frequenz fy.
Sei v: = fy / fx das Frequenzverhältnis des geordneten Tonpaares (x, y).
Die Klasse aller Tonpaare (x,y) mit gleichem Frequenzverhältnis v heisst Intervall.
v > 1: Aufwärtsintervall. v < 1: Abwärtsintervall, v = 1: Prim,
v = 2: Oktave aufwärts, v = 1/2: Oktave abwärts.
Ein konkretes Paar (x,y) mit Frequenzverhältnis v ist ein Repräsentant des Intervalls.
(In obiger Definition werden also z.B. eine Aufwärts- und eine Abwärtsquinte als verschiedene Intervalle betrachtet.)
Addition von Intervallen:
Man definiert die Addition über eine geeignete Wahl von Repräsentanten:
(x,y) + (y,z) : = (x,z).
Beispiel: Quint + Quart = Oktave bzw. (c,g)+(g,c')=(c,c').
Satz: Zu (x,y) gehöre das Frequenzverhältnis v, zu (y,z) das Frequenzverhältnis w.
Dann gehört zu (x,y)+(y,z)=(x,z) das Frequenzverhältnis v⋅w.
In Worten:
Der Addition zweier Intervalle entspricht die Multiplikation ihrer Frequenzverhältnisse.
Beispiel: Quint + Quart = Oktave ↔ (3/2)⋅ (4/3) = (2/1).
Das Frequenzverhältnis v eines Intervalls widerspiegelt die physikalische Ebene. Jedem Intervall i lässt sich aber auf der Hör-Ebene (der "Empfindungsebene") auch eine Grösse in Oktaveinheiten O zuordnen, das Oktavmass des Intervalls i:
Das Oktavmass sagt aus, "wieviele Oktaven gross" das Intervall ist:
r O-Einheiten oder r O (r = reelle Zahl).
Beispiele: Prim: 0 O, Oktave: 1 O, Doppeloktave: 2 O.
Zusammenhang zwischen dem Oktavmass und dem Frequenzverhältnis v:
| r = Anzahl Oktavschritte O (Oktavmass), additiv | 0 | 1 | 2 | 3 | 4 | |||
| ↑ lb(v) | ↓ 2r | |||||||
| Frequenzverhältnis v multiplikativ |
1 | 2 | 4 | 8 | 16 |
Pro Oktavschritt aufwärts verdoppelt sich das Frequenzverhältnis. Die Anzahl Oktavschritte eines Intervalls ist gleich lb(v).
lb(v) ist dabei der Zweierlogarithmus von v ("Logarithmus binarius").
Beispiel: Quinte: v = 3/2, Oktavmass: lb(3/2) O ≈ 0.58496... O. (Die Quint ist also etwas mehr als eine halbe Oktave gross.)
Neben dem Oktavmass O verwendet man noch eine kleinere Einheit: "Cent" (ct):
1 O = 1200 ct. (Der Klavierhalbton der gleichstufigen Stimmung hat dann 100 ct.)
Beispiel: Quinte: 0.58496... O ≈ 701.955 ct. (Das sind etwa 7 "moderne" Halbtöne.)
Intervall ↔ v ↔ lb(v) O = 1200⋅lb(v) ct
Der Zweierlogarithmus des Frequenzverhältnisses v ist das Oktavmass des Intervalls. 1 O = 1200 ct.
Unterwirft man einen Punkt gleichzeitig zwei senkrecht aufeinander stehenden harmonischen Schwingungen (Schwingung 1 in x-Richtung, Schwingung 2 in y-Richtung), so beschreibt der Punkt eine Lissajous-Figur. Je nach Frequenzverhältnis der beiden Schwingungen und je nach Phasenverschiebung entsteht eine andere Figur. So entstehen Bilder von musikalischen Intervallen: Oktave: 2 : 1, Quinte: 3 : 2, Quarte: 4 : 3, usw.
Rechts: Modell eines mechanischen Lissajous-Zeichners:
1. Kurbelnocken
2. Räder (Frequenz a bzw. Frequenz b)
3. Gleiter, bewegt in x- bzw. y-Richtung durch den Kurbelnocken
4. Leiste zur Erhöhung des oberen (blauen) Gleiters
5. Zeichenstift in der Kreuzung der beiden Gleiter-Schlitze
6. Papier
7. Führungsleisten für die Gleiter
8. Schlitze in den Gleitern, in welche die Kurbelnocken eingreifen
Dreht man die Räder mit Frequenz a bzw. Frequenz b z.B. im Gegenuhrzeigersinn, greifen die Kurbelnocken, an denen man dreht in die Schlitze der Gleiter. Diese bewegen sich deshalb analog einer harmonischen Schwingung in x- bzw. y-Richtung.
Im Kreuzungspunkt beider Schlitze wird ein Stift angebracht. Dieser führt die kombinierte Bewegung der beiden Gleiter aus. Verhalten sich die Drehfrequenzen a und b rational, entstehen geschlossene Lissajousfiguren.
Eine Computersimulation dieses mechanischen Modells liefert natürlich exaktere Bilder, ein mechanisches Modell ist jedoch bestimmt sinnenfälliger.
Falls das Applet nicht startet, ins leere Bild klicken.
Online-Lissajous-Zeichner. Falls das Applet nicht startet, ins leere Bild klicken.
Das gezeigte Computermodell kann sehr gut mechanisch nachgebaut werden:

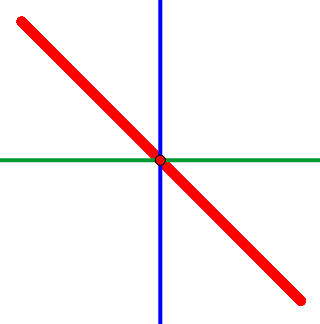
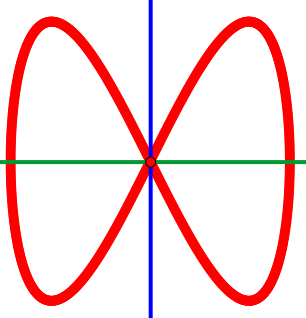
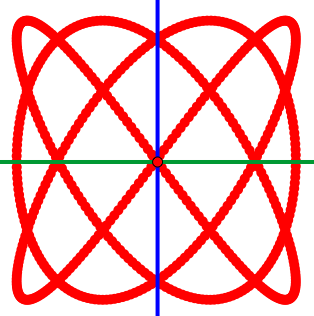


Bild links: Darstellung von Intervallen als Halbgerade y = v⋅x (v, x > 0). Der Nullpunkt gehört nicht mehr zur Halbgeraden.
x-Werte: Anzahl Schwingungen pro Sekunde Frequenz 1
y-Werte: Anzahl Schwingungen pro Sekunde Frequenz 2.
v = Frequenzverhältnis ("Frequenz 2" / "Frequenz 1").
dunkelrot: Aufwärtsoktave 2 : 1, orange: Abwärtsoktave 1 : 2
dunkelbraun: Aufwärtsquinte 3 : 2, hellbraun: Abwärtsquinte 2 : 3
dunkelgrün: Aufwärtsquarte 4 : 3, hellgrün: Abwärtsquarte 3 : 4
blau: Prim 1 : 1
Die Steigung ist das Frequenzverhältnis des Intervalls. Die Halbgerade
y = v⋅x
(v, x > 0) stellt das Intervall dar. Ein Punkt (x | y) auf der Halbgeraden stellt einen Repräsentanten des Intervalls dar (ein konkretes Tonpaar).
Aufgrund der mathematischen Tatsache, dass es kein endliches Tonsystem geben kann, das allein auf reinen Quinten und gleichzeitig auf reinen Oktaven beruht, entstanden im Lauf der Geschichte viele verschiedene Tonsysteme, welche diese "Unvollkommenheit" auf je eigene Art verarbeiteten. Die drei wichtigsten Systeme waren:
-die pythagoräische Stimmung beruhend auf reinen Quinten und reinen Oktaven
-die reine Stimmung beruhend auf reinen Quinten, reinen Terzen und reinen Oktaven
-die gleichstufige Stimmung beruhend auf dem Halbton mit dem Frequenzverhältnis der zwölften Wurzel aus 2.
Intervallräume kann man auf einem Punktgitter aufbauen.
Am Beispiel der pythagoräischen Stimmung sieht das so aus:
Man startet mit einem Grundton (dieser Ton entspricht dem Intervall einer Prim mit der Verhältniszahl v = 1). In horizontaler Richtung erzeugt man nach rechts Aufwärtsoktaven (Frequenzverdoppelung, v = 2, 4, 8, usw.) und nach links Abwärtsoktaven (Frequenzhalbierung). In vertikaler Richtung erzeugt man nach oben reine Aufwärtsquinten (Multiplikation mit 3/2) und nach unten Abwärtsquinten (Division durch 3/2 bzw. Multiplikation mit 2/3).
Es entsteht ein Punktgitter, in dem jeder Punkt mit einer Verhältniszahl v ausgestattet ist.
Die Punkte haben nun eine doppelte Bedeutung:
- Wählt man für den roten Ausgangspunkt einen konkreten Ton (z.B. "c"), so entspricht jedem Punkt ein weiterer Ton. Die Verhältniszahl gibt das Frequenzverhältnis v des Intervalls vom roten Startton zum entsprechenden Ton an.
- Man kann den Punkt demnach auch als "dieses Intervall" interpretieren.
Das Punktgitter der pythagoräischen Stimmung basiert auf den beiden Grundintervallen Oktave und reine Quinte und ist zweidimensional.
Nun muss man eine endliche Auswahl an Punkten mit 1 ≤ v ≤ 2 treffen (d.h. man wählt Töne innerhalb der ersten Oktave aus) und kann damit eine Tonleiter generieren.
Wie viele solche Töne man auswählt, bleibt zunächst einmal offen.

Pythagoräischer Punktraum "reine Oktaven - reine Quinten"
Man kann die Punkte dieses Raumes mit ihren "Ortsvektoren" identifizieren (Nullpunkt ist der rote Punkt mit den Koordinaten (0|0)) und hat dann eine Art "Vektorraum". Der Unterschied zu einem richtigen Vektorraum besteht darin, dass die Skalare (hier die Werte x und y) nur aus dem Ring der ganzen Zahlen stammen (und nicht aus dem Körper der rationalen oder reellen Zahlen). Eine solche Struktur wird Modul genannt (Betonung auf dem "o").
Bild links: Der Punktraum der pythagoräischen Stimmung Die orange markierten Gitterpunkte haben einen Wert zwischen 1 und 2 und liegen als Intervalle bezogen auf den Startton innerhalb der 1.Oktave. Die Zahlen bei den Punkten geben das Intervallverhältnis v bezogen auf den roten Grundton an. Das Gitter kann beliebig weit ausgedehnt werden; es entstehen immer mehr Intervalle und damit auch immer mehr "orange" Punkte innerhalb der 1. Oktave. In der Praxis muss man bei einer bestimmten endlichen Anzahl "oranger" Punkte aufhören und diese zu einer Tonleiter zusammenfassen. Wählen wir als roten Startton c, so ergibt sich die orange Reihe aufwärts wie folgt (Quintenzirkel aufwärts): Nach unten ergibt sich die Reihe (Quintenzirkel abwärts bzw. Quartenzirkel aufwärts) |
In der pythagoräischen Stimmung, die so entsteht, treten viele weitere Intervalle auf, z.B. des-cis. Wir berechnen unten das Frequenzverhältnis- und das Cent-Mass dieses Intervalls.
Wählt man den rot gefärbten Punkt als Nullpunkt des Punktgitters mit den Koordinaten (0|0), so berechnet sich die Frequenzverhältniszahl v des Punktes (x|y) zu
v(x,y) =
2x⋅(3/2)y.
Der pythagoräische Tonraum ist also lediglich auf den Primzahlen 2 und 3 aufgebaut. Das Frequenzverhältnis jedes Intervalls hat die Form 2x-y⋅ 3y.
Das Differenzintervall zwischen zwei Punkten hat als Frequenzverhältnismass den Quotienten der Frequenzmasse der beiden Punkte: v = v2 / v1 . Das ergibt:
v(Δx,Δy) = 2Δx⋅(3/2)Δy
Beispiel:
Wir starten mit dem Ton c (Prim, roter Punkt).
"des" entspricht dann dem Punkt mit den Koordinaten (3 | -5).
"cis" entspricht dann dem Punkt mit den Koordinaten (-4 | 7).
Intervall des-cis:
2-4-3⋅ (3/2)7-(-5) = 2-7⋅ (3/2)12 ≈ 1.01364... = pythagoräisches Komma.
Centmass: 23.46 ct.
Das "cis" ist also in pythagoräischer Stimmung um das pythagoräische Komma oder um 23.46 ct (knapp ein Viertel eines Halbtonschrittes) höher als das "des".
Das pythagoräische Komma im Pythagoräischen Punktraum oben:
Der Punkt mit den Koordinaten (-7 | 12) entspricht (als Intervall-Ortsvektor aufgefasst) dem pythagoräischen Komma. Es ist v(-7| 12) =
2-7⋅(3/2)12 ≈ 1.01364...
Oktavmass: 0.01955 O = 23.46 cent.
Anmerkung
Es ist v(x,y) =
2x⋅(3/2)y. Um zum Oktavmass zu gelangen, haben wir den Zweierlogarithmus dieses Ausdrucks zu nehmen. Wir erhalten:
lb[2x⋅(3/2)y] = lb[2x-y⋅3y] = (x - y)⋅lb(2) + y⋅lb(3) = (x - y) + y⋅lb(3).
Oktavmass(x,y) = (x - y)⋅lb(2) + y⋅lb(3) = (x - y) + y⋅lb(3).
Das Oktavmass jedes Punktes in der pythagoräischen Stimmung entsteht somit als ganzzahlige Linearkombination von lb(2) = 1 und lb(3) und ist für y≠0 irrational.
Das Centmass ergibt sich als 1200⋅[ (x - y) + y⋅lb(3)].
Beispiel:
(-1 | 2), der Punkt mit dem Frequenzverhältnismass 9/8, hat das Oktavmass
-3 + 2⋅lb(3) O ≈ 0.1699... O und das Centmass 203.9 cent.
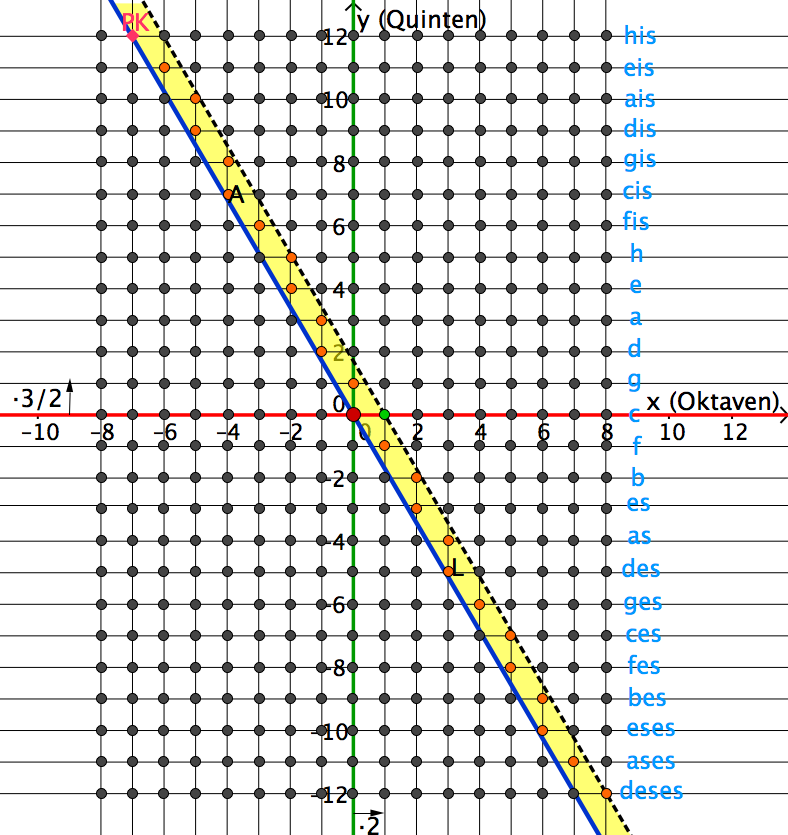
Das Oktav-Quint-Punktgitter der pythagoräischen Stimmung
Aufgaben:
1. Man finde die Gleichung der Geraden, welche v(x,y) = 1 darstellt (explizite Form).
2. Man finde die Gleichung der Geraden, welche v(x,y) = 2 darstellt (explizite Form).
Punkt (0 | 0): Prim (z.B. c - c). Die orangen Punkte stellen Intervalle innerhalb einer einzigen Grundoktave dar (1 ≤ v < 2).
Das Punktgitter ist unbegrenzt. Es entstehen immer neue Intervalle.
Rechts sind hellblau die Notennamen bezogen auf den Grundton c notiert (ohne Berücksichtigung der Oktavhöhe).
PK = Pythagoräisches Komma (Intervallverhältnis von c-his)
L = Limma (c - des) = Pythagoräischer Halbton
A = Apotome (c- cis) = "anderer" Halbton (=Ganztonschritt minus Limma)
Berechnung der Intervall-Verhältniszahl v aus den Punktkoordinaten (x | y):
v(x,y) = 2x⋅(3/2)y = 2x-y⋅3y.
Die blau eingezeichnete lineare Funktion stellt die Grenze dar zwischen Aufwärtsintervallen (v > 1) und Abwärtsintervallen (v < 1).
Gleichung: y = - (log(2) / log(3/2))⋅x .
Achtung: PK liegt nicht auf dieser Geraden, sondern etwas rechts davon (dieses "his" ist ein wenig höher als ein "c"); genauer: Mit Ausnahme von (0|0) liegt kein weiterer Punkt des Gitters auf dieser Geraden; die Gerade schafft es, bis ins Unendliche durch den Wald von Punkten zu laufen, ohne je einen dieser Punkte zu treffen.
Der Punkt (7|-12) (ein "deses") liegt ganz wenig links der Geraden. Dieses "deses" ist ein wenig tiefer als ein "c".
Die gestrichelt eingezeichnete lineare Funktion trennt Intervalle mit Verhältnis <2 von solchen mit Verhältnis >2. Sie verläuft durch den grünen Punkt (1|0) und sonst durch keinen weiteren Gitterpunkt. Im gelben Korridor zwischen den beiden gezeichneten linearen Funktionen befinden sich die Töne -oder besser: die Aufwärtsintervalle- der gewählten Grundoktave (Reoktavierungsbereich).
Umkehraufgabe: Gegeben v(x,y), gesucht x und y. Infolge der Eindeutigkeit der Primfaktorzerlegung ist diese Umkehraufgabe eindeutig lösbar. Beispiel:
Welcher Punkt hat das Intervallverhältnis 1/1944 ?
Lösung:
Wir zerlegen 1944 in Primfaktoren: 1944 = 23 ⋅ 35 .
⇒ 1/1944 = 2-3 ⋅ 3-5 ⇒ x - y = -3 und y = -5 ⇒ x = -8, y = -5 ⇒ (-8 | -5)
Wichtige Intervalle der pythagoräischen Stimmung
o = Oktave, q = reine Quinte 3 : 2
Im pythagoräischen Tonraum ist jedes Intervall eine Linearkombination von Oktave o und reiner Quinte q, d.h. hat die Form x⋅o + y ⋅q (x, y ganze Zahlen).
| Intervall | x⋅o + y ⋅q | (x | y) | v (Frequenzverhältnis) | Cent-Mass |
| Oktave | 1 o + 0 q | (1 | 0) | 2 : 1 | 1200 |
| Quinte | 0 o + 1 q | (0 | 1) | 3 : 2 | 702 |
| Ganzton (Tonos) | -1 o + 2 q | (-1 | 2) | 9 : 8 | 204 |
| pyth. grosse Terz (Ditonus) | -2 o + 4 q | (-2 | 4) | 81 : 64 | 408 |
| Quarte | 1 o - 1 q | (1 | -1) | 4 : 3 | 498 |
| pyth. Halbton (Limma) | 3 o - 5 q | (3 | -5) | 256 : 243 | 90 |
| Ganzton - Limma = anderer Halbton (Apotome) |
|
(-4 | 7) | 2187: 2048 | 114 |
| pyth.Komma | -7 o + 12 q | (-7 | 12) | 531441:524288 | 23 |
Bemerkung:
Man sieht, dass man die reine Quarte nie durch lauter Aufwärtsquinten (und Re-Oktavierungen) erzeugen kann, denn Aufwärtsquinten und Re-Oktavierungen erzeugen nur Zweierpotenzen als Nenner, während die reine Quarte den Faktor 3 im Nenner hat. Um im pythagoräischen Tonsystem z.B. ausgehend vom Grundton c den Ton f zu erzeugen, muss man also einen Quintensprung abwärts gefolgt von einem Oktavensprung aufwärts (oder umgekehrt) durchführen. Man benötigt somit auch Abwärtsquinten.
Sei t der pythagoräische Ganztonschritt 9 : 8 (t = Tonos).
Sei l der pythagoräische Halbtonschritt 256: 243 (l = Limma).
Dann ist t - 2 l das pythagoräische Komma. D.h. Ganztonschritt minus 2 Halbtonschritte ergeben eine kleine Differenz zum Grundton.
a = t - l heisst Apotome. Es ist der "andere" Halbtonschritt.
3 t + l = q = reine Quint.
Auswahl von 5 Tönen (Pentatonik):
z.B. c → g → d → a → e oktaviert: c - d - e - g - a - c'
Auswahl von 7 Tönen (Heptatonik; Diatonik) mit einem anfänglichen Quintsprung abwärts:
f ← c → g → d → a → e → h oktaviert: c - d - e - f - g - a - h - c'.
Aufgabe:
Man untersuche die Halbtonschritte in der Heptatonik links (siehe Punkteraum oben). Ebenso: Ganztonschritte.
Lösung:
e - f: (4/3) : (81/64) = 256/243
h - c': 2 : (243/128) = 256/243
Ganztonschritte: 9/8.
Jedes Intervall ist eine Linearkombination x⋅o + y ⋅q + z ⋅t
x, y, z ganze Zahlen,
o = Oktave 2 : 1, q = reine Quinte 3 : 2, t = reine grosse Terz 5 : 4.
Das Punktgitter wird 3-dimensional.
Es gibt in diesem System einen grossen (9 : 8) und einen kleinen (10 : 9) Ganzton.
Zwei grosse Ganztöne würden die reine grosse Terz um das sogenannte syntonische Komma übersteigen.
Dieses beträgt
2 grosse Ganztöne minus reine grosse Terz = 4q - 2o - t = 81/80 oder 22 cent.
Das syntonische Komma ist auch der Unterschied zwischen den beiden Ganztönen:
(9/8) : (10/9) = 81/80.
Aufgabe: Man bestimme die Koordinaten (x | y | z) des syntonischen Kommas.
Lösung: (-2 | 4 | -1)
Hat ein Punkt im Gitter die Koordinaten (x | y | z), so ist
v(x,y,z) = 2x⋅(3/2)y⋅(5/4)z.
Dieses System baut auf den Primfaktoren 2, 3 und 5 auf.
Tonstruktur der reinen Stimmung
Kurzaufbau der reinen Stimmung:
horizontal: Von C aus Quintsprung nach unten und nach oben
vertikal: zu F, C, G die reine grosse Terz (5/4) und die Quinte (3/2) bilden
F ← C → G
A E H
C G D
Dann entsteht die reine diationische, heptatonische Skala C D E F G A H C'.
Unter dem folgenden Link findet man Weiteres zur reinen Stimmung (Euler-Ebene, Kommatas, Auswahl von Tonleitertönen):
Weiteres zur reinen Stimmung
Vergleich pythagoräische Stimmung / reine Stimmung
pythagoräisch: c d e f g a h c'
9/8 9/8 256/243 9/8 9/8 9/8 256/243
rein: 9/8 10/9 16/15 9/8 10/9 9/8 16/15
Die Struktur beider Skalen ist:
|----------------------|--------|----------------------|
reine Quarte Sekund reine Quarte
Zwei Tetrachorde sind über eine Sekund miteinander verbunden.
Link zu einem pdf-Artikel von Prof. Dr. Peter Galllin zur diatonischen Tonleiter
Bereits im 16. Jahrhundert befasste sich Marin Mersenne mit 19- und 31-Ton-Systemen, ebenso Christiaan Huygens. Mersenne studierte auch ein 53-Ton-System. Um 1700 herum war ein ähnliches System in China gebräuchlich.
Warum gerade die Zahl 53 in Frage kommt, wird weiter unten erklärt.
Links:
mikrotonale Systeme
Zur 19-stufigen Stimmung
Zu Tonsystemen allgemein
Pentatonik
China
Tour d'horizon zu Tonsystemen
Eine gute Einführung liefert ferner:
Prof. Siegfried Krauter, PH Ludwigsburg: "Einführung in die Endliche Geometrie"
("Einführung in die Endliche Geometrie" anwählen)
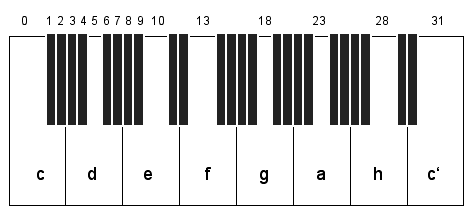
31-Ton-Klaviatur. Die Töne 0 - 10 - 18 - 25 bilden einen perfekten Dominantseptakkord

Wir betrachten unser gebräuchliches, gleichstufig temperiertes 12-Ton-System (Equal Tempered System 12, ETS12). Wir betrachten die Töne "modulo 12", d.h. wir "identifizieren" c, c', c'', usw. Auch die Intervalle betrachten wir modulo 12, d.h. eine None identifizieren wir wieder mit einer Sekunde, eine Dezime mit einer Terz, usw. Wir können auch sagen: Wir reoktavieren alles in eine einzige "Grundoktave" hinein.
Im ETS12 haben wir dann 12 Intervalle; Oktave und Prim werden identifiziert.
Allgemein: Im ETSn haben wir n Intervalle.
| c cis d dis e f fis g gis a b h c' 0 1 2 3 4 5 6 7 8 9 10 11 0 |
Intervalle berechnen wir als Differenzen der Tonnummern. Dabei rechnen wir modulo 12 (analog dem Rechnen mit Uhrzeiten): 2 - 5 = 9, usw. Jedes der 12 Intervalle erhält eine Grössenzahl von 0 bis 11 (0 = Prim bzw. Oktave, 1 = Halbtonschritt, usw.).
Betrachten wir eine Transposition um 4 Intervallstufen, d.h. um 4 Halbtonschritte ("grosse Terz"): Wir addieren zu jeder Tonnummer 4 und rechnen modulo 12, d.h. z.B. 10 + 4 = 2 (analog dem Rechnen mit Uhrzeiten: Beim Überschreiten der 12 beginnen wir wieder bei 0). Aus der chromatischen Skala wählen wir nun lediglich die Töne der Durtonleiter aus (schwarz und rot gedruckt), zunächst C-Dur, nach dem Transponieren E-Dur.
c cis d dis e f fis g gis a b h c'
0 1 2 3 4 5 6 7 8 9 10 11 0
|------------------------| |------------------------|
|----–--------------–––|
e f fis g gis a b h c cis d dis e
4 5 6 7 8 9 10 11 0 1 2 3 4
Wir sehen folgendes: Das Intervall der Grösse 4 ("grosse Terz") kommt in der Tonmenge der C-Dur-Tonleiter oben drei Mal vor (0 --- 4, 5 --- 9, 7 --- 11). Dann kommen auch die drei Töne mit den Nummern 4, 9 und 11 in E-Dur wieder vor (die übrigen vier werden verändert: E-Dur hat vier #) . Wir finden:
| Die Anzahl gemeinsamer Töne zwischen transponierten Tonleitern ist gleich der Anzahl des Auftretens des Transpositions-Intervalls in der Ausgangs-Tonleiter (Satz von Milton Babbitt). |
Wir suchen nun aus dem System ETSn eine Teilmenge mit folgender Eigenschaft: Wenn man alle möglichen Differenzen der Elemente dieser Teilmenge bildet (wieder modulo n gerechnet), sollen alle n Intervalle von ETSn entstehen.
Aufgabe: Man finde in ETS12 eine solche Teilmenge.
Lösung: Eine mögliche Lösung wäre {1, 3, 6, 7}. Mit 4 Elementen kann ich auf 4⋅3 Arten Differenzen ≠ 0 bilden, dazu kommt noch die Differenz 0. Allgemein: Mit k Elementen ergeben sich k(k - 1) + 1 Differenzen.
Mit unserer Teilmenge ergeben sich folgende Intervalle:
1 - 3 = 10
1 - 6 = 7
1 - 7 = 6
3 - 1 = 2
3 - 6 = 9
3 - 7 = 8
6 - 1 = 5
6 - 3 = 3
6 - 7 = 11
7 - 1 = 6
7 - 3 = 4
7 - 6 = 1
x - x = 0
Es kommen also alle 12 Intervalle vor. Einen Schönheitsfehler hat dieses Beispiel jedoch: Das Intervall der Grösse 6 ("Tritonus") kommt zwei Mal vor. Mit k = 4 ergibt unsere Formel k(k - 1) + 1 ja auch den Wert 13; wir erhalten 13 Intervalle, also muss mindestens eines doppelt vorkommen.
Wir suchen nun Teilmengen, die beim Bilden aller möglichen Differenzen zwischen ihren Elementen alle Intervalle genau ein Mal erzeugen. Eine solche Teilmenge heisst Differenzenmenge oder besser Intervallbasismenge.
Aufgabe: Für welche natürlichen Zahlen n hat ein ETSn-System überhaupt die Chance, eine solche Basismenge zu besitzen?
Lösung: Die Bedingung lautet: k(k - 1) + 1 = n.
| k 1 2 3 4 5 6 7 n 1 3 7 13 21 31 43 |
Unsere Teilmenge {1, 3, 6, 7} wäre eine Basismenge in ETS13. Sie würde modulo 13 jedes der 13 Intervalle genau einmal erzeugen. Weitere Beispiele für Basismengen:
{0, 1, 3} oder auch {0, 4, 6} in ETS7
{0,1,4,6,13,21} oder auch {0,10,18,25,27,30} in ETS31.
Bemerkung: Die Mengen {0, 1, 3} und {0, 4, 6} sind "Gegenmengen", d.h.
{0, 4, 6} = {-0, -3, -1} modulo 7.
Analoges gilt für das zweite Beispiel.
Es liegt nun nahe, die n Töne in Form von Punkten und die n Intervalle in Form von Linien zwischen den Punkten darzustellen. Das führt auf eine geometrische Darstellung, die man endliche projektive Ebene nennt.
Beispiel: ETS7: 7 Töne (0, ... , 6), 7 Intervalle (0, ... , 6).
Eine endliche projektive Ebene besteht aus einer endlichen Anzahl von Punkten und
einer endlichen Anzahl von Linien mit folgenden Eigenschaften:
P1: Durch jedes Punktepaar geht genau eine Linie
P2: Jedes Linienpaar hat genau einen Schnittpunkt.
P3: Es gibt ein Viereck (Reichhaltigkeits-Axiom).
Es gilt ferner:
Jede Linie enthält gleich viele, nämlich k, Punkte.
Jeder Punkt liegt auf genau k Linien.
Daraus folgt: Es hat insgesamt k(k - 1) + 1 Punkte und k(k - 1) + 1 Linien.
Für ETS7 entsteht die Fano-Ebene (rechts). {0, 1, 3} ist wieder eine erzeugende Differenzenmenge. Wir betrachten folgendes Blockschema:
0 1 2 3 4 5 6
1 2 3 4 5 6 0
3 4 5 6 0 1 2
Eine Spalte entspricht je einer Basismenge, respektive in der Fano-Ebene einer Linie.
Von einer Spalte zur nächsten gelangt man durch Addition von 1 (modulo 7). Das Blockschema hat die Eigenschaft, dass jedes Punktepaar genau in einer Spalte vorkommt. (Das ist Axiom P1 von oben.) Beispiel: (2, 5) kommt genau in der 3. Spalte vor. Von den (7 tief 2) = 21 möglichen Punktepaaren sind pro Spalte 3 vorhanden; in den 7 Spalten kommen alle 21 möglichen Paare genau einmal vor.
Man sieht auch, dass je 2 Spalten genau eine Zahl gemeinsam haben (Axiom P2).
[Dies folgt aus der Tatsache, dass jede Spalte jedes Intervall genau ein Mal erzeugt zusammen mit dem Satz von Babbitt: Die transponierte und die ursprüngliche Spalte haben dann genau ein Element gemeinsam.]
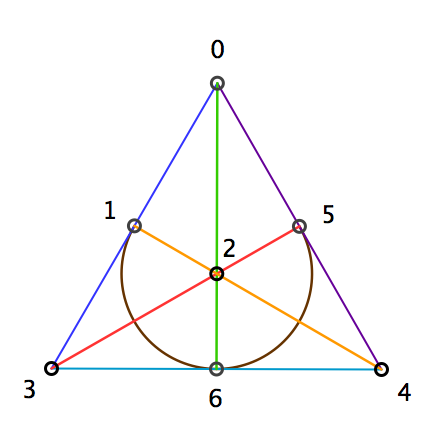
Fano-Ebene: 7 Punkte, 7 Linien (je anders gefärbt). Die Zahlen der drei Punkte auf einer Linie erzeugen jeweils in Form der verschiedenen Differenzen alle Intervalle von ETS7. (k - 1) ist die Ordnung der projektiven Ebene; hier ist die Ordnung also 2.
Nicht jedes ETSn mit n = k(k - 1) + 1 hat eine solche projektive Darstellung. Eine solche Darstellung haben ETS7, ETS13 und ETS31, nicht aber ETS43.
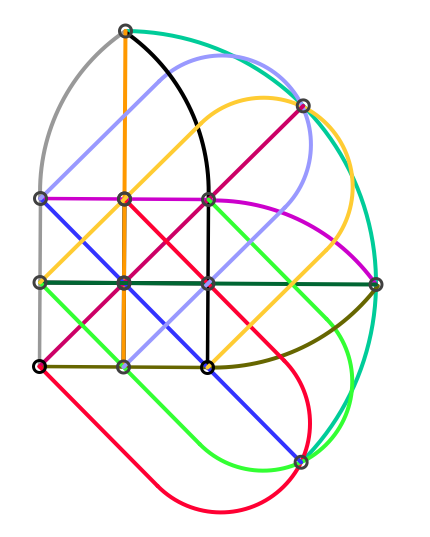
Projektive ETS13-Ebene, k = 4, Ordnung der Ebene = 3
Man kann obiges Netz als U-Bahnnetz einer Stadt interpretieren. Die Axiome für eine endliche projektive Ebene besagen dann:
P1: Von jeder Station aus kann man, wenn man will, ohne umzusteigen an jede Zielstation gelangen.
P2: Jede U-Bahn-Linie kreuzt jede andere Linie an genau einer Haltestelle.
P3: Es gibt Rundreisen mit Benützung von 4 U-Bahn-Linien.

Mikrotonales Xylofon von Harry Partch
Quellen:
http://de.wikipedia.org/wiki/Harry_Partch
http://de.wikipedia.org/wiki/Mikrotonale_Musik
Ab dem 19. Jahrhundert löste sich das musikalische Schaffen von der Fixierung auf einen Grundton. Anstelle der Beziehung zu einem Grundton trat eine Beziehung zu einer Skala oder zu einer Tonreihe. Beispiele:
-Ganztonskala (von Debussy oft verwendet)
-12-Tonreihe nach Schönberg
Andere Parameter als lediglich die Frequenz eines Tones wurden wichtig: Tonfarbe, Ausdruckswert (bis hin zum Einbezug von Geräuschen), Kontrast, Variationen, usw.
Analoge Lösungen von alten Bindungen finden sich z.B. auch in den bildenden Künsten und in der Literatur.
Die Skalenentwicklung via reine Quinten geht so vor sich:
Man startet mit einem Grundton und geht in Quinten aufwärts (⋅3/2), wobei man gegebenenfalls re-oktaviert (⋅1/2), wenn der neue Ton über die Grundoktave hinausgeht. Das Verfahren endet, wenn man nach x Quintensprüngen und y Re-Oktavierungen wieder beim Startton landet, formal:
(3/2)x⋅(1/2)y = 1 ⇔ 3x / 2x+y = 1 ⇔ 3x = 2x+y ⇔ x log(3) = (x + y) log(2) ⇔
(x+y) / x = log(3) / log(2).
Wir wissen, dass für ganzzahlige x und y keine Lösung existiert (eine ganzzahlige Dreierpotenz kann keine ganzzahlige Zweierpotenz sein). Wir suchen Näherungsbrüche für (x+y) / x = log(3) / log(2).
x = Anzahl Tonleitertöne pro Oktave, y = Anzahl Re-Oktavierungen im Laufe des Quintenschichtungs-Algorithmus.
Hier kommt das Verfahren der Kettenbruchentwicklung einer reellen Zahl zum Zug. Wir zeigen es am Beispiel log(3) / log(2) ≈ 1.58496... Als Hilfsmittel genügt ein Taschenrechner:
1.58496... =
1 + 0.58496... = 1 + r1 . Nun berechnen wir
1/ r1≈ 1 + 0.7095... = 1 + r2 . Nun berechnen wir
1/ r2≈ 1 + 0.4094... = 1 + r3 . Nun berechnen wir
1/ r3≈ 2 + 0.44247... = 2 + r4 . Nun berechnen wir
1/ r4≈ 2 + 0.2600... = 2 + r5 . Nun berechnen wir
1/ r5≈ 3 + 0.8459... = 3 + r6 . Nun berechnen wir
1/ r6≈ 1 + 0.18216... = 1 + r7, usw.
Setzen wir dies alles zusammen, folgt:
log(3) / log(2) = 1 + 1 / (1/r1) = ... =
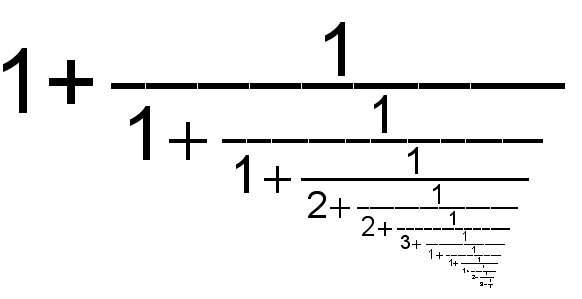
Werten wir diesen Kettenbruch stückweise aus, ergeben sich folgende Näherungsbrüche für log(3) / log(2):
1 2 3/2 8/5 19/12 65/41 84/53
x = 5 12 41 53
y = 3 7 24 31
Wir sehen, dass die übliche 12-Teilung der Oktave dem Ideal nahe kommt (12 Quinten ergeben ungefähr 7 Oktaven; Abweichung = pythagoräisches Komma ≈ 23.46 cent). Die nächsten guten Teilungen wären 41 und 53 (53 Quinten sind ungefähr 31 Oktaven; Abweichung nur noch ≈ 3.62 cent).

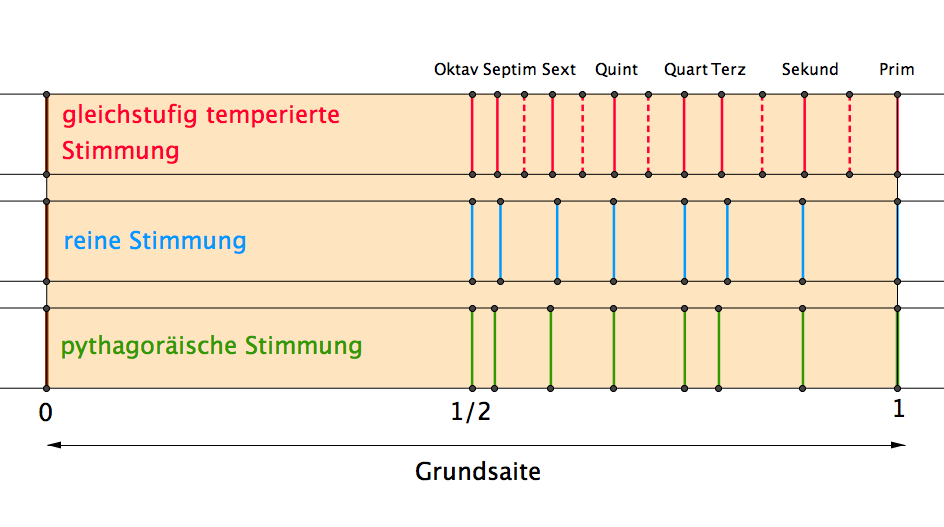
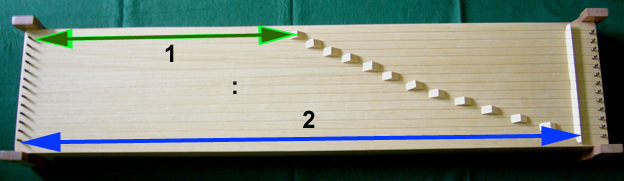
Bild links: Vergleich von drei Stimmungen an der Stellung von Monochord-Reitern. Die massgebliche Saitenlänge verläuft vom linken Steg (braun) zum Reiter (rot, blau, grün).
Oben: gleichstufig-temperierte Stimmung. Man erkennt die sehr genaue Annäherung der Quinten (700 cent) an die reine und die pythagoräische Stimmung (702.0 cent).
Mitte: reine Stimmung (reine Quinten und reine Terzen). Die reingestimmte Terz (386.3 cent) ist etwas kleiner als die gleichstufig-temperierte (400 cent).
Unten: pythagoräische Stimmung (reine Quinten). Die pythagoräische Terz (407.8 cent) ist etwas grösser als die Terz der andern beiden Stimmungen.
Ein Ton als periodische Schwingungsfunktion ist meist keine reine Sinusschwingung, sondern kann als Überlagerung einer ganzen Menge von Partialtönen dargestellt werden.
Der 1. Partialton ist der Grundton selber, der 2. Partialton (= 1. Oberton) hat die doppelte Frequenz des Grundtons (Oktave), der 3. Partialton die dreifache Frequenz (Quinte über der Oktave = Duodezime), usw.
Der n-te Partialton hat die n-fache Frequenz des Grundtons.
Diese Situation gilt allerdings z.B. bei Saiteninstrumenten nur näherungsweise, da eine reale Saite eine gewisse "Steifigkeit" aufweist. Die Partialtöne weichen deshalb von diesem Ideal ab.
Am Klavier kann man die Partialtöne experimentell veranschaulichen. Man drückt z.B. stumm die Oktave des Grundtons (z.B. c' zum Grundton c) und lässt sie gedrückt, sodass die Saite ungedämpft schwingen kann. Dann schlägt man den Grundton kurz an. Der Ton der stumm gedrückten Saite, d.h. der 2. Partialton, wird mitschwingen. Man versuche es auch mit dem stummen Drücken des 3. Partialtons.
Bemerkung: Oft spricht man vom Grundton und dem 1., 2., 3., ... Oberton. Der 1. Oberton ist der 2. Partialton, der 2. Oberton der 3. Partialton, usw. Die Nummerierung via Partialtöne passt besser zum Rechnen mit Frequenzen; der n-te Partialton hat bei einer ideal biegsamen Saite die n-fache Frequenz des Grundtons.
Schwebungen: Erklingen zwei Töne, die nur leicht auseinanderliegen, hört man ein regelmässiges An- und Abschwellen, eine sogenannte Schwebung. Die Schwebungsfrequenz entspricht der Differenz der Frequenz der beiden nahe beisammen liegenden Töne.
Will man auf einem Instrument (z.B. dem Monochord oder dem Klavier) eine Oktave rein stimmen, achtet man darauf, dass keine Schwebungen mehr vorhanden sind.
Sei der Kammerton a'440 gegeben. Man will das d' eine Quinte tiefer stimmen. Der 3. Partialton von d' ist a''. Aber der 2. Partialton von a' ist ebenfalls a''. Ist die Quinte rein gestimmt (3:2), werden der 3. Partialton von d' und der 2. Partialton von a' keine Schwebung erzeugen.
Will man nun das d' jedoch in gleichstufiger Stimmung einrichten, so gilt folgendes:
d'gleichstufig hat die Frequenz 220⋅25/12 ≈ 293.6648 Hz.
Der 3. Partialton hat die dreifache Frequenz also 880.9933 Hz ≈ 881 Hz.
Diesen 3. Partialton setzen wir nun in Hörbeziehung zum 2. Partialton von a'440, also zu a''880.
Der Unterschied ist 1 Hz. Dies wird ein geschultes Ohr als Schwebungsfrequenz hören (ein An- und Abschwellen im Sekundentakt). Ist dies der Fall, hat man d' gleichstufig-temperiert korrekt gestimmt.
Sei y / x = pm / qn , p, q prim, p≠q, das Frequenzverhältnis eines Intervalls. Dann ist
pm x = qn y ,
in Worten:
Der pm -te Partialton vom Ton mit Frequenz λx ist gleich dem qn -ten Partialton vom Ton mit Frequenz λy.
Beispiel Quinte: 3 / 2: Der 3. Partialton des unteren Tones ist gleich dem 2. Partialton des oberen Tones.
Ein Intervall wird als "konsonant" empfunden, wenn von den beiden Tönen möglichst viele Partialtöne übereinstimmen. Der Begriff der Konsonanz ist allerdings sehr kultur- und weltbildabhängig. So spielten bei Pythagoras zahlenmystische Überlegungen eine starke Rolle.
Einfache Versuche zu Partialtönen und Schwebungen
Quelle: Berkeley Physik Kurs 3, Schwingungen und Wellen, Frank S. Crawford Jr, Vieweg, Braunschweig,Nachddruck 1979, p. 56f.
 |
- Schlagen Sie zwei Stimmgabeln der gleichen Frequenz aneinander. Halten Sie beide Gabeln in die Nähe des einen Ohrs; verändern Sie die Lage geringfügig, bis Sie Schwebungen hören. Man kann auch den einen Zinken einer der Gabeln mit einem kleinen Gummiband "beschweren". Das Gummiband kann man leicht verschieben und so verschiedene Schwebungen erzeugen. - Klavier als Analysator für Partialschwingungen (Klavier als Fourieranalysator):
- Drücken Sie einen tieferen Ton auf dem Klavier stumm nieder. Schlagen Sie dann einen höheren Ton scharf an. Ist der höhere Ton ein Partialton des tieferen, werden bei der tieferen Saite diese Partialschwingungen angeregt. Man kann sie hören, ohne dass dabei die Grundschwingung sie übertönt. |
- Ermitteln Sie auf die im letzten Versuch beschriebene Art experimentell die Partialtöne eines Tones, z.B. die ersten 6 oder 7 Partialtöne von c'.
Nun können Sie üben, einen bestimmten Partialton, z.B. b''', herauszuhören, wenn der Ton c' angeschlagen wird: Drücken Sie c' stumm. Schlagen Sie b''' scharf an. Hören Sie nun, wie b''' als 7. Partialton von c' klingt. - Nun schlagen Sie c' an und versuchen, b''' herauszuhören. Der Partialton b''' ist nicht exakt gleich dem Klaviertastenton b''' (das Klavier ist ja gleichstufig gestimmt).
- Drücken Sie c' stumm, dann c'' scharf. Sie regen damit in der c'-Saite den Partialton c'' an. Schlagen Sie nun c'' nochmals sehr leise an, angepasst an den noch angeregten Partialton. Hören Sie Schwebungen? [Die wirkliche Klaviersaite erzeugt nicht die exakten Partialtöne der Theorie, da sie eine gewisse Starrheit besitzt.]
- Schlagen Sie auf dem Klavier die beiden tiefsten Töne A27.5 und Ais29.1 sachte an. Die Schwebungsfrequenz beträgt 1.6 Hz und kann eventuell durch eine Person mit geschultem Gehör wahrgenommen werden.
Hat der Wellenträger (Saite, Flötenrohr) eine begrenzte Länge L und wird vom einen Ende her eine Welle ausgesandt, so wird sie am andern Ende reflektiert. Eine Welle läuft durch mehrfache Reflexionen auf dem Träger hin und her. Soll das System nicht zum Stillstand kommen, dürfen sich diese hin- und herlaufenden Wellen nicht gegenseitig auslöschen. Bei bestimmten, günstigen Wellenlängen bilden sich sogenannte stehende Wellen, d.h. bestimmte Stellen des Wellenträgers bewegen sich überhaupt nicht mehr (Bewegungsknoten) und andere Stellen schwingen sehr heftig (Bewegungsbäuche). Dies geschieht, wenn Wellen und reflektierte Wellen an den Rändern des Wellenträgers genau aufeinander passen.
Zwei Bewegungsknoten haben dann den Abstand einer halben Wellenlänge der hin und her laufenden Welle.
Bei Schallröhren befinden sich an den geschlossenen Enden stets Stellen ohne Bewegung (Bewegungsknoten) und an den offenen Enden Stellen mit maximaler Bewegung (Bewegungsbäuche). Mit dem Luftdruck ist es umgekehrt: An den geschlossenen Enden ist der Druck hoch, an den offenen niedrig.
Geogebra-Modell von Welle und reflektierter Welle und der Überlagerung beider Wellen.
Die Zahl n (n = 1: Grundschwingung = erster Partialton, n = 2: zweiter Partialton, usw.) kann im Applet eingestellt werden.
Rechts oben: Beidseits geschlossene Vorrichtung. Rohrlänge = halbe Wellenlänge der laufenden Schallwelle.
Rechts Mitte: Einseitig offen, einseitig geschlossen ("gedackte Orgelpfeife"):
Rohrlänge = ein Viertel Wellenlänge der laufenden Schallwelle.
Rechts unten: Beidseitig offenes Rohr ("offene Orgelpfeife"): Rohrlänge = halbe Wellenlänge der laufenden Schallwelle.
Berechnungsbeispiel:
Für die laufende Welle (hier die laufende Schallwelle) gilt: c = λ⋅f .
c = Ausbreitungsgeschwindigkeit der laufenden Welle (Schallgeschwindigkeit in Luft bei 20°C ist c = 340 m/s), λ = Wellenlänge der Schallwelle, f = Frequenz.
Wie gross sind eine offene und eine gedackte Orgelpfeife mit dem Ton A 55 Hz?
Lösung:
λ = c / f = (340 / 55) m ≈ 6.182 m.
Offene Pfeife: L = λ /2 ≈ 3.091 m
Gedackte Pfeife: L = λ /4 ≈ 1.545 m
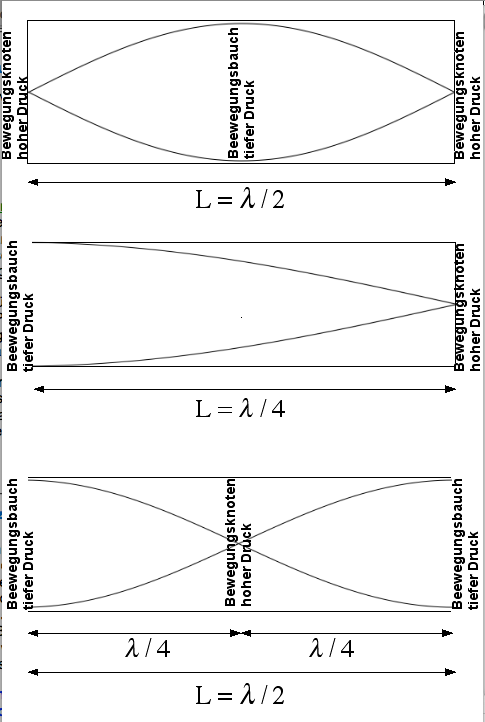
Anschaulich-heuristische Erklärung für den Zusammenhang zwischen Pfeifenlänge L und der Wellenlänge λ der abgestrahlten Schallwelle
Mit einer langen Slinky-Spiralfeder können wir folgende Versuche durchführen:
1. Zwei Personen halten die Feder je an einem Ende in ca. 3 m Abstand voneinander. Eine Person hält passiv, die andere gibt einen kurzen Druckstoss ab. Der Stoss wird bei der zweiten Person (festes Ende) reflektiert und als Druckstoss zurück zur ersten Person gesandt. Dort wird bei genügend Energie der Druckstoss eventuell erneut als Druckstoss reflektiert.
2. Gleiche Anordnung, aber diesmal zieht Person 1 kurz an der Feder retour. Dieser "Zug" wird nun ebenfalls durch die Feder zu Person 2 weitergeleitet und wird dort, am festen Ende, ebenfalls als "Zug" reflektiert und kommt so als "Zug" wieder bei Person 1 an.
3. Nun simulieren wir ein offenes Ende 2. Wir lassen ein Stück von ca. 30 cm der Feder nach unten hängen. Das untere Ende ist nun offen. Von oben geben wir einen kleinen Druckimpuls ab. Am unteren Ende wird die letzte Windung nach unten beschleunigt, infolge der Massenträgheit bewegt sie sich noch mehr nach unten und erzeugt einen Zug auf die Feder, der nun zurück reflektiert wird.
4. Ein Zug würde am offenen Ende als Druck reflektiert, wie man sich gut vorstellen kann.
Wir fassen zusammen:
Am geschlossenen Ende wird Druck als Druck und Zug als Zug reflektiert.
Am offenen Ende wird Druck als Zug und Zug als Druck reflektiert.
Nun zur heuristischen Erklärung für den Zusammenhang zwischen Pfeifenlänge L und der Wellenlänge λ der abgestrahlten Schallwelle:
1. Beide Enden geschlossen:
Vom Rand 1 her geht ein kleiner Druckimpuls weg. Er wird als Druckimpuls vom Rand 2 her reflektiert und kommt nach der Wegstrecke 2L zurück zu Rand 1, wo er erneut als Druckimpuls reflektiert wird. Schwingt die Aussenluft ebenfalls in diesem zweitaktigen Rhythmus, bleibt das System angeregt. Immer wenn ein Impuls die Strecke 2L zurückgelegt hat, erfolgt eine neue Anregung. Die Wellenlänge der abgestrahlten Schallwelle ist also 2L.
2. Beide Enden offen ("offene Pfeife"):
Von Rand 1 her erfolgt wieder ein Druckimpuls. Er wird am offenen Rand 2 als Zug reflektiert, kommt zurück zum ebenfalls offenen Rand 1 und wird dort als Druck reflektiert. Schwingt die Aussenluft in diesem Zweiertakt, bleibt das System angeregt. Wiederum beträgt die Wellenlänge der äusseren Schallwelle 2L.
3. Rand 1 offen, Rand 2 geschlossen ("gedackte Pfeife"):
Hier haben wir einen viertaktigen Zyklus: Druckimpuls von Rand 1, Reflexion dieses Druckimpulses wiederum als Druck am geschlossenen Rand 2, zurück zum offenen Rand 1, dort wird dieser Druckimpuls als Zug reflektiert, der Zug geht zurück zum geschlossenen Rand 2, dort wird dieser Zug als Zug reflektiert, geht zurück zum offenen Rand 1, wo dieser Zug als Druck reflektiert wird. Erzeugt jetzt die Aussenluft ebenfalls einen Druckimpuls, bleibt das System angeregt. Hier ist der Rhythmus also viertaktig. Die Wellenlänge zu diesem Viertakt-Rhythmus ist 4L.
Resonanzversuch
Ein Rohr von ca. 5 cm Durchmesser und etwas mehr als 20 cm Länge wird einseitig in ein Becken mit Wasser getaucht, sodass die untere Öffnung durch das Wasser verschlossen wird. Durch leichtes Anheben und Senken des Rohres kann die Länge der Luftsäule im Innern des Rohres variiert werden.
Nun regt man eine Stimmgabel mit a' 440 Hz an und hält sie über die obere Öffnung des Rohres. Bei einer bestimmten Luftsäulenlänge wird der Ton der Stimmgabel plötzlich deutlich lauter: Die Länge der gedackten Pfeife passt nun genau zur äusseren Anregung (Resonanz).
Berechnung des Vorgangs:
Es ist c = 340 m/s, f = 440 Hz ⇒ λ = c / f ≈ 0.773 m ≈ 77.3 cm. Dies ist nach den Überlegungen oben gleich der 4-fachen Rohrlänge L. Es ergibt sich L = 19.3 cm.
Das experimentelle Ergebnis weicht leicht von diesem Wert ab, da die schwingende Luftsäule etwas aus dem Rohr heraus ragt.