Die Vorzeichenregeln bei Addition und Subtraktion positiver und negativer Zahlen

Wir betrachten folgende vier Aufgaben. Wir beginnen mit einem Start-Saldo a und addieren oder subtrahieren ein Guthaben (+5) oder eine Schuld (-5):

1) a + (+5) =

2) a + (-5) =

3) a - (+5) =

4) a - (-5) =

Aufgabe 1: Zum Saldo a kommt ein Guthaben (+5) hinzu. Schluss-Saldo: a + 5

Aufgabe 2: Zum Saldo a "erbten" wir eine Schuld (-5). Unser Saldo verringert sich. Schluss-Saldo: a - 5. (Man kann auch Schulden erben!)

Aufgabe 3: Vom Saldo a gaben wir ein Guthaben (+5) weg. Unser Saldo verringert sich. Schluss-Saldo: a - 5.

Aufgabe 4: Vom Saldo a wurde uns die Schuld (-5) weggenommen. Unser Guthaben vergrössert sich. Schluss-Saldo: a + 5.

Bei all diesen Überlegungen spielt es keine Rolle, ob der Anfangs-Saldo a im Plus oder im Minus war.

Wir unterscheiden Operationszeichen und Vorzeichen:

Das Vorzeichen gibt an, ob wir es mit einem Guthaben oder mit einer Schuld zu tun haben. Das Operationszeichen gibt an, ob wir etwas bekommen oder etwas abgeben. Dabei können wir sowohl Guthaben wie Schulden bekommen oder abgeben.

Ein "rhythmischer" Zugang zu den Vorzeichenregeln bei der Multiplikation ganzer Zahlen

1)

(+3) * (+4) interpretieren wir ganz natürlich als Verdreifachung des Guthabens (+4). Resultat: (+12).

2)

(+3) * (-4) interpretieren wir ebenfalls ziemlich natürlich als Verdreifachung der Schuld (-4). Resultat: (-12).

Wir können diese Aufgabe aber auch "rhythmisch" angehen:

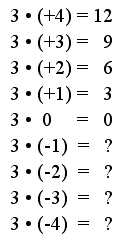
Die Ergebnisfolge verringert sich von oben nach unten bei jeder Rechnung um 3. Führen wir diese Reihe fort, so ergeben sich folgende Ergebnisse:

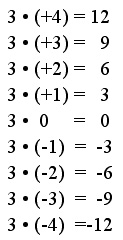
Damit finden wir wieder dasselbe Ergebnis: 3 * (-4) = -12.

3)

(-3) * (+4) =

Erste Überlegung: Die Multiplikation ist kommutativ, d.h. die Rechnung muss dasselbe Ergebnis liefern wie die Rechnung (+4) * (-3) und das ist nach den Überlegungen oben gleich -12 (Vervierfachung der Schuld (-3)).

Zweite Überlegung: rhythmisch: Die Ergebnisse in der folgenden Aufgabenreihe vermindern sich jeweils um 4. Das ergibt folgende rhythmische Fortsetzung der Reihe:

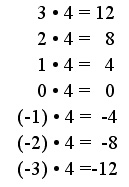
Wir erhalten dasselbe Resultat wie durch die Überlegung mit dem Kommutativgesetz.

4)

(-3) * (-4) =

Hier finden wir keine sinnvolle Einkleidung mit Guthaben und Schulden. Wir überlegen deshalb rein "rhythmisch":

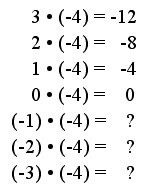
Die Ergebnisse werden -von oben nach unten betrachtet- von Rechnung zu Rechnung um 4 grösser. Wir erhalten somit, wenn wir die Reihe im gleichen Rhythmus fortsetzen, folgende Ergebnisse:

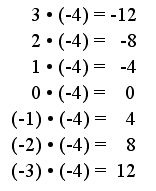
Damit ergibt sich die Regel "Minus mal Minus gleich Plus" auf diesem "rhythmischen" Weg zwingend.

Das "Verminusdreifachen" einer Schuld verwandelt diese in ein dreifaches Guthaben: (-3) * (-4) = +12.

Umgekehrt verwandelt das "Verminusdreifachen" ein Guthaben in dreifache Schulden: (-3) * (+4) ? -12.

Diese rhythmische Art der Erweiterung bekannter Operationen auf neue Zahlbereiche (hier Erweiterung der Multiplikation auf negative Zahlen) werden wir später wieder antreffen beim Erweitern der Operation des Potenzierens auf negative und rationale Exponenten.

Zusammenfassung

Addition und Subtraktion:

a + (+b) = a + b: Addition von Guthaben

a + (-b) = a - b: Addition einer Schuld

a - (+b) = a - b: Subtraktion von Guthaben

a - (-b) = a + b: Subtraktion einer Schuld

Multiplikation (und Division):

(+a) * (+b) = (+ab)

(+a) * (-b) = (-ab)

(-a) * (+b) = (-ab)

(-a) * (-b) = (+ab)

Dann wäre z.B. (-1)*(-1) = (-1).

Dann liesse sich nach der Binomischen Formel folgern:

0² = 0 = (1 + (-1))² = 1² + 2*1*(-1) + (-1)(-1).

Wenn aber der letzte Summand (-1)(-1)in obigem Auseruck gleich (-1) wäre, folgte 2*1*(-1) = 0 oder 2*(-1)=0 oder nach Division durch 2:

(-1) = 0: ein Widerspruch.