Viele Integrale lassen sich nur durch numerische Näherungen lösen. Die Simpsonregel ist eine solche Näherungsmethode.
Die nachfolgend beschriebene gewichtete Trapezregel (Simpsonregel), welche die Fläche zwischen einem Funktionsgraphen und der x-Achse von aussen und von innen "einquetscht", hat eine besondere Eigenschaft:
Im Fall einer quadratischen (und sogar einer kubischen) Funktion liefert diese Regel den exakten Integralwert in einem Intervall [a;b].
Die Regel wird zunächst am besten anhand einer konkaven Funktion dargestellt:

Beispiel: y = -x2 + 4.
Wir betrachten ein Intervall [a; b], ein Sehnentrapez (gelb) und ein Tangententrapez (gelb plus orange zusammen). m ist die Mitte zwischen a und b, d.h. m=(a+b)/2.
Sei As der Flächeninhalt des Sehnentrapezes und At derjenige des Tangententrapezes.
Der Flächeninhalt zwischen Parabel und x-Achse im Intervall [a;b] liegt zwischen At und As.
Satz: Im Falle der quadratischen Parabel durch die Punkte (a,f(a)), (m,f(m)) und (b,f(b)) liefert das gewichtete Mittel dieser beiden Flächeninhalte (Tangententrapez doppelt gewichtet) den exakten Integralwert zwischen a und b.
Die gewichtete Trapezregel (Simpsonregel):

Für k < 0 (konvexe Parabel) gilt die Rechnung ebenfalls. Die geometrische Anschauung ist jedoch bei konvexen Funktionen nicht mehr in jedem Fall so eindeutig gegeben wie bei konkaven Funktionen:
Im Bild links werden die Trapeze zerstört.
Wir können uns behelfen, indem wir die Parabel links um ein passendes Stück c nach oben schieben (Bild rechts), bis die Trapeze wieder erscheinen. Die Integralfläche hat sich dabei um c(b-a) vergrössert.
Wenden wir auf die nach oben verschobene Parabel die Simpson-Regel an, sehen wir sofort, dass sie ebenfalls einen um c(b-a) vergrösserten Wert gegenüber der Parabel links ergibt. Somit funktioniert die Regel auch für die Parabel links, obwohl dort keine unmittelbar einsichtige geometrische Evidenz mehr vorhanden ist.


Links: y =
x2 (Trapeze zerstört), rechts y = x2 + 2 (Trapeze wieder hergestellt)
Gewichtete Trapezregel (Simpsonregel) für beliebige, hinreichend gutmütige Funktionen:
Für Funktionen, die "hinreichend gutmütig" sind, etwa solche, die sich in eine Taylorreihe entwickeln lassen, dient die Simpson-Regel als gute Näherung, denn in einem genügend schmalen Teilintervall lässt sich der Funktionsgraph gut quadratisch annähern, d.h. als Stück einer quadratischen Parabel auffassen.
Wie könnte ein Algorithmus aussehen, der die Integralfläche hinreichend genau annähert, und wie sähe ein Stopp-Kriterium für einen solchen Algorithmus aus?
Zuerst definiert man eine gewünschte Genauigkeit G für das zu berechnende Integral.
Ist bereits |At - As| < G, kann man den Algorithmus beenden.
Falls nicht, unterteilt man das Intervall [a;b] in zwei gleich grosse Teilintervalle [a;m1] und [m1;b] und wendet auf jedes Teilintervall die Simpson-Regel an. Für jedes Teilintervall prüft man, ob |At - As| < G/2 ist.
Wenn ja, bricht man das Verfahren ab, wenn nein, unterteilt man die beiden Teilintervalle erneut in je zwei weitere Teilintervalle und prüft, ob für jedes der neuen, kleineren Teilintervalle |At - As| < G/4 ist, usw.
Der Vorteil
eines Algorithmus', der die Integralfläche von aussen und von innen "einquetscht" gegenüber einem solchen, der z.B. nur innere oder nur äussere Trapeze verwendet, liegt auf der Hand: Man hat ein gutes Stoppkriterium, das an eine gewünschte Genauigkeit gekoppelt ist.
Auch für kubische Funktionen integriert die Simpson-Regel exakt:
Beispiel: f(x) = -0.5x3 + 2x2 - x + 2
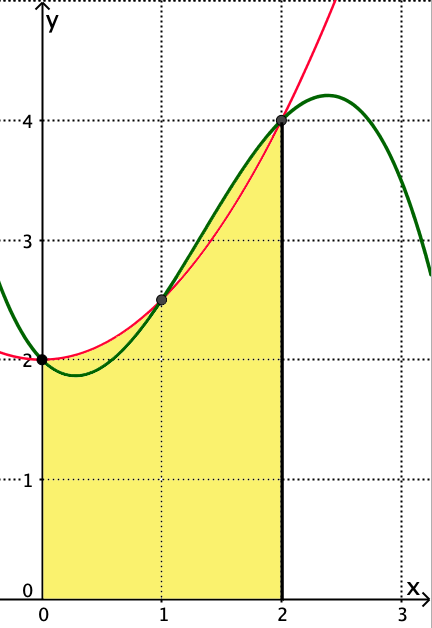
Simpsonregel für den Flächeninhalt unter der grünen (und auch der roten) Kurve im Intervall [0;2]:
(2/6)⋅(2 + 4⋅2.5 + 4) = 16/3.
grün: f(x) = -0.5x3 + 2x2 - x + 2
Wir betrachten z.B. das Intervall [0 ; 2] (gelb markiert).
rot: Wir legen eine Näherungsparabel g(x) durch die Punkte (0/2), (1/2.5) und (2/4):
Ansatz: g(x) = ax2 + bx + c. Punkte einsetzen:
0a + 0b + c = 2
1a + 1b + c = 2.5
4a + 2b + c
= 4
Es folgt a = 0.5, b = 0, c = 2, somit:
g(x) = 0.5x2 + 2
Man verifiziert:
g(x) integriert mit den Integrationsgrenzen 0 und 2 die Funktion f(x) exakt. Der Integralwert beträgt in beiden Fällen 16/3. Denselben Wert liefert die Simpsonregel! Auch sie integriert mit diesen Integrationsgrenzen die kubische Funktion f(x) exakt!
Verändert man das betrachtete Intervall, muss auch g(x) verändert werden. Der Graph von g(x) verläuft stets durch den Anfangspunkt (a; f(a)) des Intervalls, den Mittelpunkt (m;f(m)) und den Endpunkt (b;f(b)). Die quadratische Funktion g(x) muss jedoch gar nicht berechnet werden; es genügt, die Simpson-Formel anzuwenden!
Zusammenhang mit der Keplerschen Fassregel
Der Astronom und Mathematiker Johannes Kepler (1571 - 1630) entwickelte seine Fassregel, nachdem er anlässlich seiner Hochzeit Zweifel an der Volumenbestimmungs-Methode des Weinhändlers hatte. Dieser hatte nämlich einfach einen Stab durchs Spundloch des Weinfasses geführt und ihn diagonal ins Fass gesenkt und daraus das Volumen "erschlossen". Diese Methode erschien Kepler falsch, da sie von den Dimensionen des Fasses abhängig war.
So entwickelte er seine eigene "Fassregel", um das Volumen eines Fasses zu bestimmen.
Kepler nahm dabei an, das Randkurvenprofil des (liegenden) Fasses sei eine Parabel, die durch die drei Punkte A, M und B (siehe Bild) gegeben sei. Diese Parabel rotiert um die x-Achse.
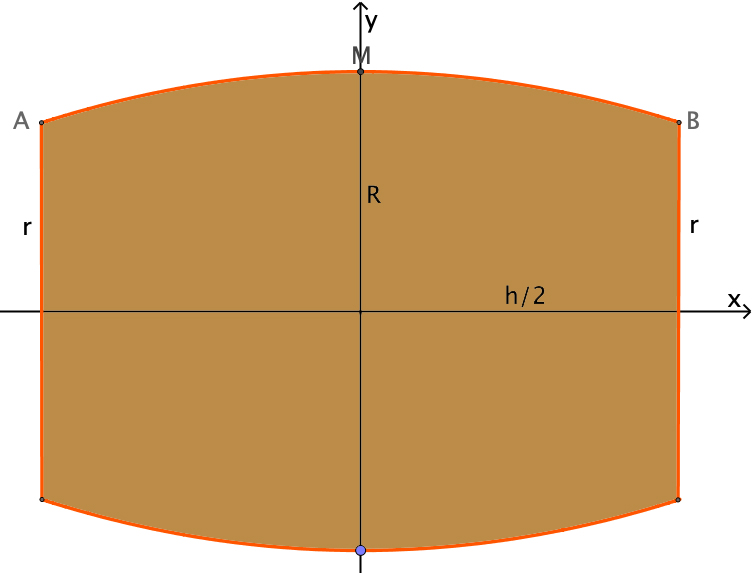

Sei A1 die Bodenfläche, Am die Mittelfläche und A2 die Deckfläche des Fasses.
Diese Flächen lassen sich leicht aus den Radien r und R (bzw. dem Umfang in der Fassmitte) berechnen.
Sei h die Höhe des Fasses.
Keplers Fassregel lautet analog zur Simpson-Regel:

Beispiel:
Sei (Bild links) A(-50 / 20), M(0 / 40), B(50 / 20),
d.h. r = 20 cm, R = 40 cm, h = 100 cm.
Die Näherungsformel ergibt ein Volumen von ca. 376'991 cm3 = 376.991 Liter.
Der genauere Volumenwert beträgt 360.326 Liter (siehe exakte Formel unten).
Die Schätzung ist somit ca. 4.6% zu hoch.
Herleitung des exakten Volumens
(siehe Schnitt-Bild des Fasses oben):

Vom zweitletzten zum letzten Schritt macht man gleichnamig und multipliziert aus.
Zur Herleitung links:
Herleitung der Volumenformel für ein liegendes Fass; Parabel durch A, M und B.
In der Praxis ermittelt man R via Umfang in der Fassmitte.
Zunächst wird die Parabelfunktion f(x) ermittelt.
Für die Volumenformel denkt man sich das liegende Fass in unendlich viele senkrechte Scheiben mit Breite dx und Radius f(x), d.h Volumen dV = f(x)2πdx, zerlegt.
V ist dann das Integral von -h/2 bis h/2 von dV bzw. das doppelte Integral von 0 bis h/2 von dV..
Austesten der Formel an Spezialfall:
Für r = R entsteht die Volumenformel für den Kreiszylinder: V = π⋅h⋅R2.
Vergleich der Näherungsformel (Fassregel) mit der exakten Formel:
Sei V*:= (hπ/3)⋅(R2 + 2r2). Sei V= (hπ/15)⋅(3r2+4Rr+8R2).
Man zeige: V*/V ≥ 1, d.h. V* überschätzt V ein wenig.
(Für r = R wird V* = V, d.h. der Fehler beträgt 0%. Der maximale Fehler entsteht bei r=0 und beträgt 25%.)
Rotation einer Fläche um die y-Achse (quadratisches Paraboloid):
Man berechne das Volumen einer handgezogenen Kerze in Form eines Paraboloids, die 9 cm hoch ist und unten einen Kreisdurchmesser von 6 cm hat.
Die halbe Kerze ist im Bild hellblau dargestellt.
Wir lassen die blaue Parabelfläche um die y-Achse rotieren. Es entsteht die Paraboloid-Kerze:

Die rote Umkehrfunktion rotiert um die x-Achse.
orange: Grundfläche 9π, Mittelfläche 4.5π, Deckfläche = 0.
Um die Volumenformeln, welche stets von einer Rotation um die x-Achse ausgehen, anwenden zu können, müssen wir die hellblaue Parabelfunktion an der Winkelhalbierenden y=x (gestrichelt) spiegeln, d.h. die Umkehrfunktion (rot) betrachten.
Diese Umkehrfunktion lautet: g(x) = (9 - x)0.5.
Wir betrachten das Intervall [0, 9].
Die Keplersche Näherungsformel betrachtet die Grundfläche, die Mittelfläche und die Deckfläche (die hier = 0 ist). Es ist h = 9. Sei V* der Volumenwert via Näherungsformel.
Die Näherungsformel lautet:
V* = (h/6)⋅(Grundfäche + 4⋅Mittelfläche + Deckfläche)
Wir erhalten
V* =
(9/6)⋅(9π + 4.5π + 0) = 81π/2.
Die exakte Formel über das Integral π⋅g(x)2 (von 0 bis 9) liefert ebenfalls 81π/2.
Die Näherungsformel integriert somit hier exakt:
Wir können deshalb bei einem quadratischen Paraboloid (hellblau) direkt die Näherungsformel anwenden, indem wir die Grundfläche, die Mittelfläche und die Deckfläche (hier = 0) betrachten und das Volumen über die Formel
V* = (h/6)⋅(Grundfäche + 4⋅Mittelfläche + Deckfläche)
berechnen. Wir können uns deshalb den Umweg über die Umkehrfunktion und das Integral sparen.
Antwort zur Kerzenaufgabe:
Die Kerze hat ein Volumen von ca. 127 cm3.