
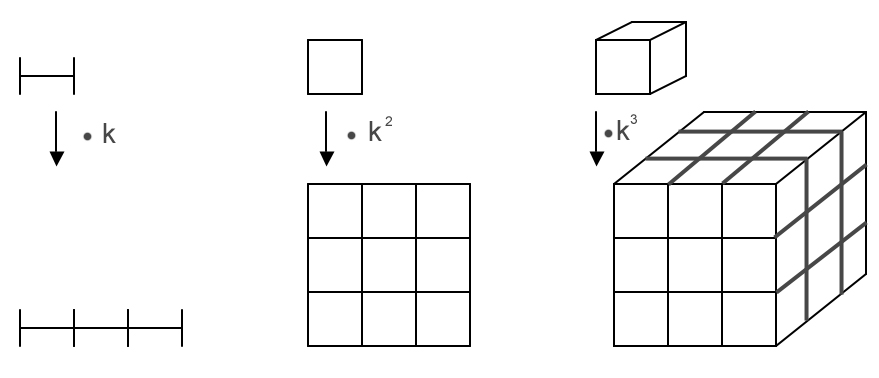
Werden die Längen eines Gebildes mit dem Faktor k gezoomt, so zoomt sich die Fläche mit dem Faktor k2 und das Volumen bzw. das Gewicht mit dem Faktor k3 .
Dies hat weitgehende Folgen für das richtige Mass von Lebewesen wie bereits 1928 J.B.S. Haldane, ein englischer Naturforscher und Zeitgenosse Darwins, herausfand (On being the right, size).

Aufgaben:
2. In Märchen und Sagen kommen Riesen vor. Wenn die Hand einer Person ca. 500 ml Volumen aufweist, wie gross ist dann das Volumen der Hand eines Riesen, der die zehnfache Länge der Person hat? |
3. Hier eine Überlegung des englischen Naturforschers J.B.S. Haldane, eines Zeitgenossen von Darwin (um 1928): Ein Mensch, der aus dem Wasser steigt, trägt im Moment des Aussteigens auf sich noch einen Wasserfilm von ca. 0.3 mm Dicke; das sind ca. 500 g Wasser, d.h. etwa 1/140 des Körpergewichts. 4. Um bei Warmblütern die Körpertemperatur halten zu können, muss die Wärmeabstrahlung via Körperoberfläche durch Nahrungszufuhr kompensiert werden. Die zugeführte Nahrungsmenge muss deshalb etwa proportional zur Körperoberfläche sein (und nicht zum Gewicht). Vergleichen Sie Körpergewicht und Körperoberfläche eines Menschen und eines Mini-Wesens (z.B. eines Mäuschens) das z.B. 40-mal kleiner ist als ein Mensch. |
Das Zusammenspiel zwischen Längen, Flächen und Volumina unserer Organe und unserer Körperteile funktioniert nur in genau der Grösse, die wir haben ("on being the right size"). Menschliche Riesen oder Zwerge wären nicht lebensfähig. Auch Tiere sind in ihrer Grösse genau ihrem Lebensraum angepasst. Sie haben für diesen Lebensraum genau die richtige Grösse und das richtige Verhalten (z.B. Vogelzug bei Einzug der kalten Jahreszeit).
Lösungen:
1.
k = 1.75 m / 1.65 m = 1.061, d.h. Längenzuwachs = 6.1%.
k2 = 1.125, d.h. Flächenzuwachs = 12.5%.
k3 = 1.193, d.h. Volumen- und damit auch Gewichtszuwachs = 19.3%.
2.
k = 10. k3 = 1000 => Volumen der Riesenfaust = 1000 ⋅ 500 ml = 500 L.
Sie hat also (bei einer Dichte von 1.2 g / cm3 ) eine Masse von mehr als 500 kg, dies an einem „Hebelarm“ von ca. 6 m Länge. Der Riese könnte seine eigene Hand gar nicht anheben, zudem würden beim Anheben vorher seine Armknochen brechen, da die Stabilität eines Knochens proportional zur Querschnittsfläche ist. Bei wachsendem k vermag die Querschnittsfläche dem stärker wachsenden Volumen und Gewicht der Faust nicht mehr zu folgen; der Knochen bricht unter dem Gewicht der eigenen Faust.
3. k = 1/20, k2 = 1/400, k3 = 1/8000.
Die Oberfläche des Mini-Wesens ist 400-mal kleiner als die Oberfläche eines Menschen => Das kleine Wesen trägt bei gleicher Wasserfilmdicke ca. 500 g / 400 = 1.25 g Wasserfilm auf sich.
Die Körpermasse ist jedoch 8000-mal kleiner als unsere, also ca. 70 kg : 8000 = 8.75 g. Das kleine Wesen trägt also einen Wasserfilm, der etwa 1/7 seines Körpergewichts ausmacht!
(Das wäre, wie wenn wir einen Wasserfilm von 10 kg tragen müssten: Wir könnten unter dem Gewicht dieser Masse nicht mehr aus dem Wasser aussteigen und müssten ertrinken.)
Bei noch kleineren Dimensionen wird das zu tragende Wassergewicht sogar grösser als das eigene Körpergewicht; dies ist z.B. bei Insekten der Fall, die ins Wasser fallen. Deshalb kann ein nasses Insekt nicht mehr wegfliegen; der Wasserfilm ist zu schwer.
J.B.S. Haldane („On being the right Size, 1928) schreibt: |
4. k = 40, k2 = 1'600, k3 = 64'000. Nehmen wir an, der Mensch habe eine Masse von 80 kg und esse täglich 1 kg Nahrung. Das kleine Wesen hat eine Masse von 80 kg : 64'0000 = 1.25 Gramm. Sein Nahrungsbedarf ist jedoch proportional zu seiner Körperoberfläche. Es muss also etwa 1600-mal weniger Nahrung aufnehmen als ein Mensch, d.h. ca. 1/1600 kg = 0.625 Gramm. Das ergibt eine benötigte Nahrungsmenge, die der Hälfte des eigenen Körpergewichts entspricht. Eine Maus frisst tatsächlich je nach Art 1/4 bis 1/1 ihres Körpergewichts an Nahrung. In kalten Regionen, wo der Wärmeverlust via Körperoberfläche gross ist, muss eher noch mehr Nahrung zur Kompensation aufgenommen werden. Deshalb sind in kalten Regionen kleine Tiere nicht optimal.
J.B.S. Haldane schreibt hierzu: |
