Bombellis mechanische Vorrichtung zur Lösung der kubischen Gleichung x³ - px - q = 0

Textquelle:
Federica La Nave: Deductive Narrative and the Epistemological Function of Belief in Mathematics - On Bombelli and Imaginary Numbers, in: Circles disturbed, The Interplay of Mathematics and Narrative, Apostolos Doxiadis, Barry Mazur, Princeton University Press, 2012, p. 79 ff.

Direkt zum Geogebra-Modell von Bombellis Apparatur:
hier

Grundlage

Die kubische Gleichung ax³ + bx² + cx + d = 0 lässt sich zunächst einmal in die Normalform
x³ + b'x² + c'x + d' = 0 bringen (a = 1). Durch Substitution
x = y - b'/3 entsteht y³ + py + q = 0, eine kubische Gleichung ohne quadratischen Teilterm.

Beispiel: Aus x³ - 9x² + 33x - 65 = 0 entsteht y³ + 6y - 20 = 0.

Es genügt also, eine Lösungsformel für y³ + py + q = 0 zu finden.

Niccolo Tartaglia (ca. 1500 - 1557) fand folgende Lösungsformel ("Formel von Cardano", die jedoch nicht von Geronimo Cardano, sondern von Tartaglia stammt):

Die reduzierte Gleichung x³ + px + q = 0 hat eine Lösung x₁:

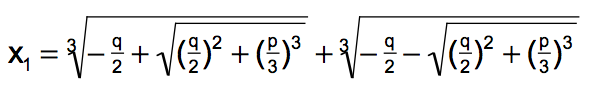
Hat man eine Lösung x₁ gefunden, kann man die kubische Gleichung durch (x - x₁) dividieren und erhält eine quadratische Gleichung, die man mit der bekannten abc-Formel auflösen kann. Je nach Wert der Diskriminante dieser quadratischen Gleichung entstehen weitere reelle Lösungen oder -in heutiger Terminologie- komplexe Lösungen.

Jede kubische Gleichung hat mindestens eine reelle Lösung, denn für negative x-Werte mit grossem Betrag ist
x³ + px + q negativ, für positive x-Werte mit grossem Betrag ist
x³ + px + q positiv. Dazwischen muss es folglich einen reellen x-Wert geben, für den
x³ + px + q genau 0 wird.

Beispiel: Man löse x³ - 15x - 126 = 0 mit Hilfe der Cardano-Formel.
Man findet eine reelle Lösung x₁ = 6. Nach Division
(x³ - 15x - 126) : (x - 6) entsteht x² + 6x + 21 = 0 mit den -in heutiger Terminologie- komplexen Lösungen -3 + 2i√3 und -3 - 2i√3.

Probleme bereitete jedoch der Fall, wo in der Cardano-Formel der Ausdruck unter der Quadratwurzel negativ war. Dies stellte die Mathematiker um 1550 vor Probleme, da das Konzept der komplexen Zahlen nicht zur Verfügung stand.

Beispiel: x³ - 9x - 9 = 0. Die Cardanische Formel ergibt

Quadratwurzeln aus negativen Zahlen sah man um 1550 eigentlich als "sinnlose" Gebilde an. Trat etwa in der abc-Formel für die Quadratische Gleichung dieser Fall auf, sagte man einfach, dass die Gleichung keine Lösung habe; die entsprechende Parabel -das sah man ja auch geometrisch- hatte keinen Schnittpunkt mit der x-Achse.
Im Fall der kubischen Gleichung x³ - 9x - 9 = 0 trat jedoch etwas für die damaligen Mathematiker Irritierendes auf: Die Cardano-Formel lieferte "sinnlose" Ausdrücke (Quadratwurzeln aus negativen Zahlen), die Gleichung hat jedoch drei reelle Lösungen.
F. Vieta konnte diesen Fall etwa 100 Jahre später, also etwa um 1600 herum, mit Hilfe von Winkelfunktionen lösen. Für die Mathematiker um 1550 war dieser Fall der "casus irreduzibilis".

Rafael Bombelli (1526 - 1572) begann jedoch mit diesen "sinnlosen" Gebilden zu rechnen, indem er einfach Rechenregeln für den Umgang mit √(-1) aufstellte.
√(-1) bezeichnen wir heute als imaginäre Einheit i und definieren: i² = -1.
Obige Lösung lautet dann:

Wie aber zieht man aus einem solchen Gebilde die dritte Wurzel?
Ansatz: Wir suchen ein Gebilde der Form a + bi mit (a + bi)³ = 4.5 + i√6.75.
Mit der Rechenregel i² = -1 für das "Gebilde" i ergibt sich
(a + bi)³ = a³ + 3a²bi + 3ab²i² + b³i³ = [a³ - 3ab²] + [3a²b - b³]i.
Es ist also
(1):   a(a² - 3b²) = 4.5 und
(2):   b(3a² - b²) = √6.75
Eine relle Lösung x₁ ergibt sich als (a + bi) + (a - bi) = 2a. Der "seltsame" -imaginäre- Teil fällt heraus. Man müsste also a berechnen können. Das ist bei obigem Gleichungssystem schwierig (bei gewissen kubischen Gleichungen mit ganzzahligen Lösungen war es natürlich damals schon möglich, s. Bombellis Beispiel unten).
Bombelli fand nun in der nachfolgend beschriebenen Apparatur eine "mechanische" Lösung der kubischen Gleichung auch im "casus irreduzibilis": Es gab also reelle Lösungen sogar in geometrischer Veranschaulichung! Das "seltsame" Gebilde

stellte in Bombellis Holzmodell die (reelle) Länge einer Strecke dar!
Dies bestärkte Bombelli in der Überzeugung, dass dieses Gebilde eine Zahl darstellte und nicht einfach "sinnlos" war. Es war ein entscheidender Schritt Richtung Akzeptanz komplexer Zahlen. (Zum Geogebra-Modell.)

Bombellis Beispiel: x³ - 15x - 4 = 0. Die Cardano-Formel liefert:
x₁ = (2 + 11i)^1/3 + (2 - 11i)^1/3. Was ist (2 + 11i)^1/3? Obiges Gleichungssystem wird:
(1):   a(a² - 3b²) = 2
(2):   b(3a² - b²) = 11.
a = 2 und b = 1 sind Lösungen => (2 + 11i)^1/3 = 2 + i => x₁ = 2 + i + 2 - i = 4.
Fortsetzung: Polynomdivision: (x³ - 15x - 4) : (x - 4) = x² + 4x + 1 = 0.
x₂ = -2 + √3, x₃ = -2 - √3.

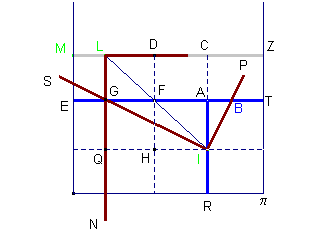
Aufgabe:

1. Man erstelle aufgrund der Beschreibung links ein Geogebra-Modell dieses mechanischen Gleichungslösers.

Beispiel hier.

2. Man beweise, dass die Vorrichtung die Gleichung x³ - px - q = 0 löst.

Die Vorrichtung liefert auch eine reelle Lösung im sogenannten "Casus irreduzibilis", d.h. im Fall, dass die Lösungsformeln von Tartaglia imaginäre Werte beinhalten.

Das Vorgehen Bombellis war kühn. Er begann mit Grössen zu rechnen, die formal noch nicht einwandfrei definiert waren. Mathematischer Fortschritt entsteht oft in dieser Weise: Man durchbricht einen bestehenden formalen Rahmen und rechnet -formal vielleicht nicht ganz sauber- mit neuen Grössen, ein Vorgehen, bei dem ein hyperkorrekter Formalist (oder ein Taschenrechner) einfach ERROR! äussern würde. Diese Art Fortschritt entsteht also gewissermassen "subversiv".
Die Differentialrechnung entstand auf ähnliche Art und Weise - ein Glück für diese Theorie, dass sie erst so spät formalisiert wurde, wie der Philosoph Imre Lakatos bemerkte, so konnte sie wuchern und Reichhaltigkeit gewinnen.

Die komplexen Zahlen, also etwa die √-1 (oder wie wir heute besser sagen: i), überschritten tatsächlich die damalige Vorstellung von "Zahl": √-1 ist nämlich ein Gebilde, das

a) nicht positiv sein kann, denn eine positive Zahl quadriert ergibt eine positive Zahl,
was für dieses Gebilde nicht zutrifft; es ergibt quadriert (-1).

b) nicht negativ sein kann, denn auch eine negative Zahl ergäbe quadriert eine positive Zahl.

c) nicht 0 sein kann, denn 0 quadriert, ergibt 0.

√-1 musste also -wie Bombelli erkannte- ein Gebilde sein, das weder positiv noch negativ noch 0 ist.

Die Bezeichnung √-1 für die imaginäre Einheit ist keine glückliche Wahl - die Einführung eines neuen Symbols "i" ist nötig. Warum?

√(-1) ⋅ √(-1) = ?
Wir wissen, dass das Resultat (-1) ist: Eine Wurzel quadriert ergibt als Resultat die Grösse, die unter dem Wurzelzeichen steht.
Andererseits kennen wir die Regel, dass man bei Multiplikation zwei einzelne Quadratwurzeln unter eine einzige Quadratwurzel zusammenfassen kann (Potenzregel):

Das ist jedoch falsch. Die Einführung des neuen Symbols "i" mit der Definition i² = -1 ist nötig, da das Symbol √(-1) auf Widersprüche führt.

Mit i wird ein neues Symbol durch eine einfache Definition ( i² = -1) eingeführt. Wenn das "so leicht" geht, kann man sich fragen, ob man nicht "ebenso locker" andere Symbole einführen könnte? Dass dies nicht "einfach so" geht, zeigt folgendes Beispiel:
Wir entscheiden uns, ein Symbol "j", einzuführen mit der Eigenschaft j ⋅0 = 1. Geht das?
Wir finden: j⋅0 = 1 = j⋅(0 + 0) = j⋅0 + j⋅0 = 1 + 1 = 2, somit 1 = 2. Damit bricht unser ganzes Zahlsystem zusammen, denn alle natürlichen Zahlen werden gleich. Unsere Erfindung ist deshalb unmöglich.
Die "Erfindung" von "i" jedoch war ein Meilenstein und eröffnete riesige neue Felder in Mathematik und Physik.

Philosophische Bemerkung

Der Philosoph Willard Van Orman Quine ("On what there is", 1948) sagt, dass mit dem Aufstellen einer Theorie auch festgelegt wird, was im Rahmen dieser Theorie existiert. Eine "gute" Theorie sollte sparsam umgehen mit den "Dingen", die sie einführt, sie sollte aber auch strukturell einfach sein, d.h. mit möglichst wenig "Aufwand" möglichst viel beschreiben können. Das eine geht manchmal auf Kosten des anderen. Am Beispiel der komplexen Zahlen lässt sich dies veranschaulichen: