1. Die Lösung ist selbst-korrigierend.
2. Vorstufe: Welche vierstellige Zahl ergibt durch 68 und durch 90 geteilt Rest 0?
3. 45
Wenig interessanter Lösungsweg: Alle Zahlen notieren und einzeln auswerten.
Besser: Venn-Diagramm:
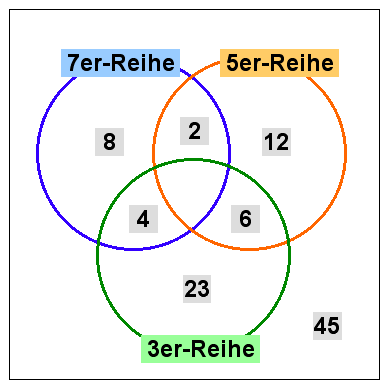
Anzahl Dreierreihenzahlen: 99 : 3 = 33
Anzahl Fünferreihenzahlen: 100:5 = 20
Anzahl Siebnerreihenzahlen: 98:7 = 14
Anzahl Fünfzehnerreihenzahlen: 6
Anzahl Einundzwanzigerreihenzahlen: 4
Anzahl Fünfunddreissigerreihenzahlen: 2
Anzahl 105er-Reihenzahlen: 0.
Mit diesen Angaben das Venndiagramm wie oben ausfüllen. Die eingefüllten Zahlen bedeuten die Anzahl der entsprechenden Zahlen von 1 bis 100.
4. Die Lösung ist selbst-korrigierend.
5. Vorstufe: Welche Zahl gibt jeweils Rest 0?
6. a) 192 Ziffern, b) 2893 Ziffern, c) 10'000
7. Zu den Stockwerken 0, 1, 2, ... gehören die Kartenzahlen
0, 3, 9, 18, 30, 45, 63, ... Aufschlussreicher sind jedoch die durch 3 dividierten Kartenzahlen : 0, 1, 3, 6, 10, 15, 21. Formel: n (n + 1) / 2. => Formel für die Kartenzahlen: 3n (n + 1) / 2. Für n = 47 ergibt sich 3384. Dies unter der Voraussetzung, dass auch zuunterst auf dem Tisch noch horizontale Karten liegen. Andernfalls wäre noch 47 zu subtrahieren.

8. Selbstkorrigierend.
9. Selbstkorrigierend.
10. Palindrom-Zahlen
Vgl. http://www.mathematische-basteleien.de.
11. 21 Zahlen
12. 364 Tage Abstand. 364 : 7 gibt Rest 0, folglich gleicher Wochentag.
13. In jedem Jahr gibt es mindestens einen Freitag, den Dreizehnten. In gewissen Jahren kommt dies bis dreimal vor.
14. s. Hinweise bei der Aufgabenstellung.
15. s. Lösungshinweise nach der Aufgabenstellung.
Reizvoller ist jedoch die Entwicklung einer eigenen "pictouresquen" Lösung. Tipp zum Problem a) : Man arbeite mit der Eigenschaft der Parität ("gerade" / "ungerade"). Ferner kann man das berühmte Schubfachprinzip (pigeon-hole principle) verwenden: Wenn man aus {1, ... , 2n} n+1 Zahlen, also mehr als die Hälfte, auswählt, ist sicher eine gerade und sicher eine ungerade Zahl dabei...
Zum Taubenschlagprinzip siehe auch Beispiele unter diesem Link.
17. Pro 1 (roter) Diagonalschritt entsteht sowohl in horizontaler wie auch in vertikaler Richtung eine Verschiebung um 1 Quadrateinheit. Wo befindet man sich im angegebenen Beispiel (x = 8, y = 5) jeweils nach 5 bzw. 8 Schritten? - Man entwickle zuerst eine Formel für a(x,y)+c(x,y) und für b(x,y)+d(x,y). Daraus entstehen dann Formeln für a(x,y), b(x,y), c(x,y), d(x,y) einzeln.
Zur Angabe von auf-, bzw. abgerundeten Ganzzahlen verwende man die Terminologie von "floor" bzw. "ceiling":
floor(3.5) = 3, ceiling(3.5) = 4, floor(4) = 4, ceiling(4) = 4.
Das Spezielle an diesem Problem ist, dass wir von der Existenz mindestens zweier Personen mit gleich vielen Kopfhaaren wissen, ohne diese Personen jedoch konkret zu kennen. (Zudem gilt ein bestimmter Zustand nur für den Bruchteil einer Sekunde, da die Personen infolge Haarausfalls ja immer wieder die Schubladen wechseln.)
Wir erhalten ein Existenz-Resultat, ohne jedoch zu wissen, wie dieses Resultat konkret aussieht.
b) Tipp: Die 11 Zahlen seien n1, ... , n11 . Wir notieren folgende Summe:
a1n1+ ... + a11n11 . Dabei wählen wir die ai aus der Menge {0, 1}. Wir haben 211 = 2048 Möglichkeiten, eine solche Summe zu bilden. Division durch 2011 ergibt der Möglichkeit nach 2011 verschiedene Reste. Teilen wir die 2048 Kombinationen in die 2011 Rest-Schubladen ein, wird mindestens eine Schublade zwei Kombinationen mit gleichem Rest enthalten.
Seien b1n1+ ... + b11n11 und c1n1+ ... + c11n11 zwei solche Kombinationen mit gleichem Rest bei Division durch 2011. Dann hat die Differenz-Kombination
(b1-c1)n1+ ... + (b11-c11)n11 den Rest 0. (bi-ci) ist aber entweder 1, 0 oder -1. Somit ist eine Kombination wie in der Aufgabe verlangt gefunden.
Auch hier erhalten wir als Resultat nur die Gewissheit, dass eine solche Kombination existiert, ohne aber bereits zu wissen, wie sie konkret aussieht.
Das IMO-Beispiel 1972:
Eine zehnelementige Menge hat 210 = 1024 Teilmengen. Jede Teilmenge erzeugt eine Summe zwischen 10+11+...+19=145 und 90+91+...+99=945.
Wir stellen uns Schubladen mit den Nummern 145 bis 945 vor, also 800 Schubladen. Die 1024 Teilmengen versorgen wir nun je nach Summe in die richtige der 800 Schubladen. Nach dem Schubladenprinzip gibt es mindestens eine Schublade mit mehr als einer Teilmenge. Seien zwei solche Teilmengen in der gleichen Schublade, also mit gleicher Summe, mit A und B bezeichnet.
In der Regel werden A und B eine Schnittmenge haben. Wir bilden nun A \ B und B \ A, d.h. entfernen von beiden Mengen die Schnittmenge. Diese neuen Mengen haben ebenfalls gleiche Summe und sind zudem disjunkt: Die Behauptung ist bewiesen: Man findet stets zwei solche Mengen. Der Beweis ist allerdings nicht konstruktiv.
Beispiel: {10, 12, 18, 19, 20, 24, 26, 70, 90, 98}. A = {10, 12, 18, 20}, B = {10, 24, 26}, beide in der Schublade mit Summenbeschriftung 60. Wir entfernen die Schnittmenge {10}:
{12, 18, 20} und {24, 26} sind disjunkt mit je Summe 50.
19. Hinweis: Was haben die Brüche a/b einer Zeile gemeinsam? Dies ergibt bereits die Pyramidenzeile...
20. a) 2(x+10)-2x = 20; b) n2 - 1 = (n-1)(n+1), d.h. faktorisierbar für n>2
c) (n+1)(n-1) + 1 = n2 <=> n2 - 1 + 1 = n2: richtig.
d) x2 + y2 = 4k + 3. Rechte Seite ungerade => x und y haben unterschiedliche Parität. Sei x gerade und y ungerade. Dann ist x2 durch 4 teilbar. Es folgt y2 = 4k - x2 + 3. Die rechte Seite dieser Gleichung ergibt bei Division durch 4 Rest 3. Die linke Seite ergibt als Quadrat einer ungeraden Zahl bei Division durch 4 jedoch Rest 1; sei nämlich y = 2r + 1 => y2 = (2r + 1)2 = 4r2 + 4r + 1, ergibt bei Division durch 4 Rest 1.
Die Gleichung y2 = 4k - x2 + 3 kann somit nicht bestehen, da sie links und rechts unterschiedliche Viererreste gibt.
e) (x - 5)(x + 5) + 25 = x2 - 25 + 25 = x2 .
21. b) rekursiv: f(n) = f(n-1) + n. Man suche dafür eine anschauliche geometrische Erklärung. Was passiert beim Zeichnen einer neuen Geraden?
Es gibt auch eine Beziehung zwischen der g- und der f-Spalte:
f(n) = f(n-1) + g(n-1). Auch dafür lässt sich eine geometrische Erklärung finden.
Die rekursive Formel f(n) = f(n-1) + n stellt eine Arithmetische Folge 2. Ordnung dar. Die direkte Formel für f(n) aus n lässt sich über den Ansatz f(n) = an2 + bn + c durch Einsetzen der ersten drei Wertepaare (0 | 1), (1 | 2), (2 | 4) finden (Gleichungssystem).
Man erhält f(n) = n(n+1)/2 + 1. Gleichwertig ist: f(n) = n(n-1)/2 + n + 1. Auch diese Formel lässt sich geometrisch-anschaulich begründen.
| n | g(n) | f(n) | r(n) |
| 0 | 1 | 1 | 1 |
| 1 | 2 | 2 | 2 |
| 2 | 3 | 4 | 4 |
| 3 | 4 | 7 | 8 |
| 4 | 5 | 11 | 15 |
| 5 | 6 | 16 | 26 |
c), d), e)
r(n) = r(n-1) + f(n-1): Diese rekursive Formel lässt sich ebenfalls geometrisch-anschaulich begründen. Wie könnte eine solche Begründung aussehen? *)
Die Werte der r-Spalte bilden eine arithmetische Folge 3. Ordnung, die durch einen kubischen Ansatz beschrieben werden kann: r(n) = an3+bn2+cn+d. Einsetzen der ersten 4 Wertepaare und Auflösen des entsprechenden Gleichungssystems liefert:
r(n) = (1/6)n3 + (5/6)n + 1. Auch diese Formel geometrisch zu "verstehen", ist sehr schwierig (wenngleich wohl nicht unmöglich). Eine bessere Ausgangslage bietet die Darstellung mittels Binomialkoeffizienten (s. Hinweis unten).
Die Zahlen der f-Spalte heissen auch "Lazy caterer's numbers": Sie stellen die maximale Anzahl Stücke eines (zweidimensional gedachten) Fladenkuchens (pancakes) dar, welche mit n Schnitten erreicht werden kann.
Die Zahlen der r-Spalte sind die "Cake numbers": Maximale Anzahl Stücke eines Cakes mit n Schnitten.
*) Z.B. so: Man stelle sich 4 farbige Plexiglas-Ebenen im Raum in zufälliger Lage vor. Eine fünfte Ebene in zufälliger Lage sei aus gewöhnlichem Schaufensterglas. Wir orientieren nun dieses Gebilde (oder uns selber) so, dass die Schaufensterglas-Ebene senkrecht vor uns steht. Dort, wo das Schaufenster die Plexiglasebenen durchschneidet, denken wir uns die Schnittkanten fluoreszierend-leuchtend.
Was sehen wir nun, wenn wir die Augen etwas zukneifen im Schaufenster? Wir sehen 4 Leuchtgeraden in allgemeiner Lage (in der Schaufenster-Ebene liegend). Diese bilden f(4) = 11 Felder. Indem wir die Glasscheibe eingefügt haben, sind also auf unserer Seite der Glasscheibe f(4) = 11 neue Raumabteilungen entstanden. Das heisst, wir finden: f(5) = r(4) + f(4) = 15 + 11 = 26.
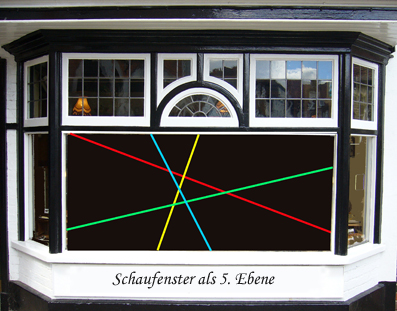
Link zur Erklärung von Pólya selber im Buch "Mathematik und plausibles Schliessen".
Weitere Hinweise in der Online-Enzyklopädie der Zahlfolgen ,
dort auch der Hinweis auf
g(n) = (n tief 0) + (n tief 1) (Natürliche Zahlen)
f(n) = (n tief 0) + (n tief 1) + (n tief 2) ("lazy caterer numbers")
r(n) = (n tief 0) + (n tief 1) + (n tief 2) + (n tief 3) ("cake numbers").
Damit ist der Weg zur Verallgemeinerung auf höhere Dimensionen offen.
Vgl. Aufgabe 14:
1, 2, 4, 8, 16, 31, 57, 99, 163, 256, 386, ...:
Numbers of regions in 4-space formed by n-1 hyperplanes.
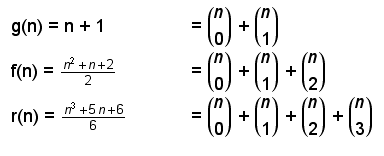
Dies ist charakteristisch für die Mathematik: Begriffe, die in völlig anderem Kontext eingeführt wurden, wirken plötzlich klärend in Gebieten, für die sie ursprünglich gar nicht gedacht waren. Eine klug gewählte Terminologie und Symbolik ist dabei sehr wichtig. - Ähnliches gilt wohl nicht nur in der Mathematik, sondern etwa auch in der Philosophie.
22.
Diophantes' Alter: 84.
ggT(851, 444) = d = ?
- 851 - 444 = 407
- 444 - 407 = 37
- 407 - 11⋅37 = 0. => d = 37.
37 = 444 - 407 = 444 - (851 - 444) = 2⋅444 - 1⋅851 =>
37 = (-1)⋅851 + 2⋅444.
a) -x + 2y = 3. Partikularlösung (z.B. erraten): (1 | 2).
Homogene Lösung: -x + 2y = 0 oder x = 2y, das heisst: x-Wert = Doppeltes des y-Wertes => Homogene Lösungen sind von der Form (2t | t).
Allgemeine Lösung = Partikularlösung + Homogene Lösungen:
(1 + 2t | 2 + t).
b) Wir stellen den ggT d=37 als Linearkombination von 851 und 444 dar:
(-1)⋅851 + 2⋅444 = 37 |⋅3. Wir erweitern die Gleichung passend:
(-3)⋅851 + 6⋅444 = 111 => Partikularlösung: (-3 | 6)
Wie unterscheiden sich 2 Lösungen voneinander?
Seien
ax + by = c und
dx + ey = c zwei Partikularlösungen. Wir bilden die Differenz =>
------------------------
(a-d)x + (b-e)y = 0.
(a-d), (b-e) sind also die Lösungen der homogenen Gleichung (der Gleichung mit c=0). Falls wir die homogenen Lösungen haben, erhalten wir alle Lösungen durch "Partikularlösung + homogene Lösungen = allgemeine Lösungen".
Homogene Gleichung: 851x + 444y = 0. Wir kürzen diese Gleichung maximal mit dem ggT und erhalten:
23x + 12y = 0 (beide Versionen haben dieselben Lösungen)
=> 23x = -12y =>
12 ist Teiler von x und 23 ist Teiler von y (warum?)
=> x = 12t und y = 23s.
Eingesetzt: 23(12t)
= -12(23s) oder gekürzt mit (23⋅12):
t = -s oder s = -t.
Wir finden als homogene Lösungen: x = 12t und y = -23t.
Allgemein: Homogene Lösungen: x = b't, y = -a't ; b' = b/d, a' = a/d.
Allgemeine Lösungen = Partikularlösung + homogene Lösungen:
(-3 + 12t | 6 - 23t).
| Allgemeine Lösungsformel für ax + by = c: x = x0 + t⋅b' und y = y0 - t⋅a' mit b' = b/d, a' = a/d, d = ggT(a,b). x0 und y0 sind Partikularlösungen. |
Siehe: Lösungsverfahren für diophantische Gleichungen ax + by = c.
IMO 1959, Nr. 1: Zeige: d = ggT von Zähler und Nenner ist 1. |
23.
a)
Teilbarkeit durch 4:
2mn ist stets durch 4 teilbar (Faktor 2 und entweder m oder n ist gerade).
Teilbarkeit durch 3:
Falls m oder n durch 3 teilbar sind, sind wir fertig. Seien nun weder m noch n durch 3 teilbar, also von der Form m = 3x+1 oder m = 3x+2 und n = 3y+1 oder n = 3y+2.
Wir quadrieren:
m2 = 9x2 +6x+1 bzw. 9x2 +12x+4 und
n2 = 9y2 +6y+1 bzw. 9y2 +12y+4.
Alle möglichen Kombinationen von m2 - n2 sind durch 3 teilbar.
Teilbarkeit durch 5:
Betrachtung der Endziffern:
m oder n durch 5 teilbar: Wir sind fertig.
Weder m noch n durch 5 teilbar: Endziffern 1, 2, 3, oder 4. Die Quadrate haben dann die Endziffern 1, 4, 9 oder 6. Bei jeder Kombination ergibt entweder die Summe oder die Differenz der Quadrate eine Zahl mit Endziffer 5 oder 0, also eine durch 5 teilbare Zahl.
d) Primzahlen p als Hypotenuse: p = 4n+1, n eine natürliche Zahl ist Hypotenuse genau eines ganzzahligen Dreiecks, p = 4n+3 jedoch nie. Beweis?
24.Wiederum gilt: Das Nachschlagen einer Lösung ohne Eigenversuche ist relativ witzlos. Trotzdem für Verzweifelte:
Interaktives Applet zum Erzeugen von Gitterpolygonen
Ein möglicher Beweis (D.E.Varberg)
Satz von Pick.
Umfassende Abhandlung hier:
http://www.m-hikari.com/ Suchstichwort "Pick" eingeben -> pdf.
25. Jedes Tripel hat folgende Eigenschaften:
- Die Vektoren haben ganzzahlige Koordinaten, d.h. als Ortsvektoren, ausgehend vom Koordinatennullpunkt, liegen ihre Spitzen auf ganzzahligen Raumgitterpunkten.
- Die Vektoren stehen paarweise senkrecht aufeinander (man teste die paarweisen Skalarprodukte, die null ergeben), bilden also drei Kanten eines Quaders.
- Die Vektoren haben ganzzahlige Länge, d.h. die Kantenlängen des durch sie erzeugten Quaders sind ebenfalls ganzzahlig.
Jedes Tripel erzeugt somit einen Quader mit ganzzahligen Eckkoordinaten und ganzzahligen Kantenlängen, einen -wie man sagen könnte- "diophantischen Quader".
Anleitung zum Erzeugen ganzzahliger Quader (pdf)
P.S. Eines der gezeigten Tripel stellt einen diophantischen Würfel dar. Welches?
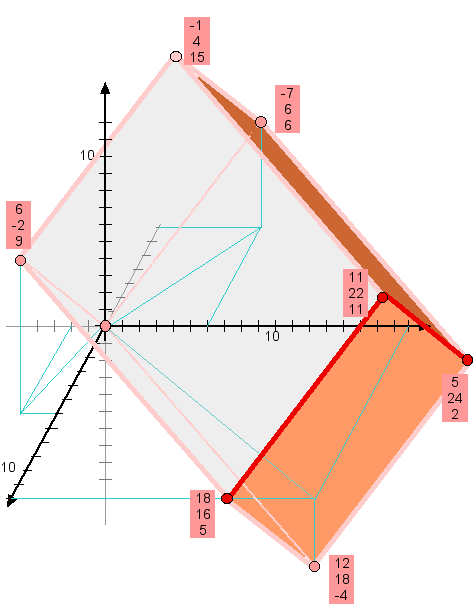
Ein Quader mit ganzzahligen Eckkoordinaten und ganzzahligen Kantenlängen.
Grafische Darstellung der diophantischen Gleichung
851x + 444y = 111
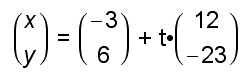
| | |
allg. Lösung = partikuläre L. + homogene L.
Die Lösungsmenge besteht aus den Punkten mit ganzzahligen Koordinaten der Geraden y = (-23/12)x + 0.25.
Ausgehend vom Punkt (-3 | 6) trägt man den Vektor [12; -23] t-mal ab, wobei t eine ganze Zahl ist.
26. Setzen Sie sich selber in die Mitte der Sechsergruppe. Um Sie herum befinden sich also noch 5 Personen. Von Ihnen aus (M) aus laufen 5 "Beziehungsgraphen" zu den übrigen Personen. Diese färben wir grün ("kennen sich bereits") oder rot ("kannten sich bisher noch nicht") ein. Nach dem Schubfachprinzip (5 Strecken in nur 2 "Farbtöpfe" tauchen) kommt eine der Farben mindestens 3-mal vor. Sei dies die grüne Farbe (ist es die rote, verläuft die Überlegung genau gleich, einfach mit vertauschten Farben). Wir haben nun die Situation von Abb. 1a. Die Personen aussen wurden dabei so angeordnet, dass die gleichfarbigen "Speichen" nebeneinander liegen.
Ist nun in der Situation von Bild 1a eine der Strecken AB oder BC ebenfalls grün (oder sind gar beide grün), sind wir fertig: Wir haben ein grünes "Cliquen-Dreieck" oder eine noch grössere Clique gefunden. Oder in Fachsprache: Wir haben einen grünen Sub-Graphen mit Ordnung ≥3 gefunden.
Sind jedoch AB und BC beide rot, liegt die Situation von Bild 1b vor. Nun ist die Frage, wie die Strecke AC gefärbt ist. Ist AC grün gefärbt, haben wir mit AMC eine grüne Dreierclique gefunden, ist AC jedoch rot gefärbt, stellt ACB eine rote Dreierclique dar.
In jedem Fall finden wir also bei 6 Personen eine grüne oder eine rote Dreierclique.
6 ist die minimale Anzahl geladener Gäste für die Existenz solcher Dreiercliquen, d.h. zu m = 3 gehört die Ramseyzahl R(m) = 6. Beachten Sie, dass unser Beweis die Minimalität der Zahl 6 nicht einschliesst. Es ist aber leicht zu zeigen, dass man mit Zahlen < 6 immer eine Situation konstruieren kann, in der es keine Cliquen von Ordnung 3 oder höher gibt.
Für die Existenz von Vierercliquen (m=4) bräuchte es bereits mindestens 18 geladene Gäste. Für höhere m gibt es bisher keine sicheren Zahlen, nur die Gewissheit, dass es eine solche minimale Zahl gibt.

27. Betrachten r = √2√2 . Ist r irrational oder rational?
Fall a) r ist rational: Wir sind fertig: Mit r = √2√2 ist eine Zahl wie verlangt gefunden.
Fall b) r ist irrational. Dann wählen wir x = r = √2√2 und y = √2. Wir bilden
xy = (√2√2)√2 = √22 = 2 (= rational). Nun ist dies eine Zahl wie verlangt.
Quelle: Proof and Other Dilemmas, MAA, Spektrum, Bonnie Gold, Roger A.Simons
Wann ist ein Problem gelöst?
Man wundert sich hier vielleicht: Wir wissen nicht, ob Variante a) oder Variante b) zutrifft, erhalten aber auf jeden Fall ein positives Ergebnis, haben also unser Problem zwar positiv gelöst, können jedoch keine konkrete Lösung angeben. (Das erinnert ein wenig ans bluffende kleine Kind, das sagt: "Ich weiss es, aber ich sage es nicht!").
Hier klaffen mathematische Existenz und konstruktiv-konkrete Existenz auseinander.
Ähnliches haben wir bestimmt schon mehrfach angetroffen. Niemand kennt alle Dezimalziffern von √2, obwohl sie "im Prinzip" eindeutig definiert sind. ("Im Prinzip" erinnert ein wenig an die alten Radio Eriwan-Witze...)
| n | 1 | 2 | 3 | 4 | 5 | 6 |
| a(n) | 1 | 1 | 2 | 6 | 18 | 65 |
siehe Online-Enzyklopädie der Zahlfolgen: A108066
Das rote Dreieck ist nicht rechtwinklig.
31.
a) Sei x die erste Zahl, y die zweite Zahl. Bsp: x = 111111, y = 222. Sei n die Anzahl Ziffern von y.
Es ist x = 100 + 101 + ... + 102n-1 = (102n - 1) / 9.
Ferner ist y =
2(100 + 101 + ... + 10n-1) = 2(10n - 1) / 9.
Dann ist x - y = (102n - 2⋅10n + 1) / 9 = [(10n - 1) / 3]2.
Bsp: Für n = 3 ergibt sich x - y = 3332.
b) Je ein Faktor 5 und ein Faktor 2 kombiniert ergeben einen Faktor 10, d.h. eine Null hinten. Faktoren 2 gibt es im Überfluss. Die Frage bleibt: Wie viele Faktoren 5 hat 100! ?
25; 50; 75 und 100 haben je 2 Faktoren 5.
5; 10; 15; 20; 30; 35; 40; 45; 55; 60; 65; 70; 80; 85; 90 und 95 haben je einen Faktor 5.
Total: 24 Faktoren 5; diese kombiniert mit je einem Faktor 2 ergeben 24 Faktoren 10, d.h. 100! endet mit 24 Nullen.
c) Der Zehnerlogarithmus der Zahl ist gleich 99⋅lg(9) = 369'693'099.6, somit hat die Zahl 369'693'100 Ziffern. Das ergäbe bei 10 Ziffern pro 1.5 cm einen Streifen von ca. 555 km Länge.
Da ist 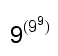 doch eine kürzere Schreibweise.
doch eine kürzere Schreibweise.
d) Endziffer 9. Mögliche Begründung:
Der Exponent ist ungerade. Eine Zahl (10x + 9)ungerade Zahl hat Endziffer 9, da als Einerziffer nur 9ungerade Zahl bleibt, und alle ungeraden Neunerpotenzen haben Endziffer 9.
33. Seien 0 der linke Punkt des Stabes, x1 und x2 die Bruchstellen (nicht unbedingt der Grösse nach geordnet) und 1 der Endpunkt des Stabes.
Damit ein Dreieck möglich ist, müssen alle Dreiecksseiten < 1/2 sein. Wir tragen die Bruchstelle x1 auf der horizontalen Achse (von 0 bis 1) und x2 auf der vertikalen Achse (zwischen 0 und 1) ab.
Genau dann, wenn das Bruchstellenpaar (x1 | x2) im grünen Bereich liegt, sind alle Dreiecksseiten < 1/2. Der grüne Bereich ist 1/4 des ganzen Einheitsquadrats.
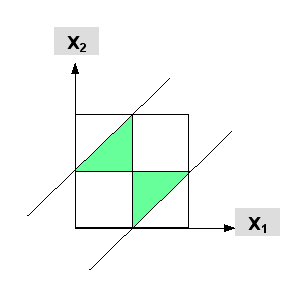
Wir erhalten somit für die gesuchte Wahrscheinlichkeit, dass ein Dreieck gebildet werden kann, den Wert 1/4.
Quelle der Aufgabenstellung: Béla Bollobás: The Art of Mathematics, Coffee Time in Memphis, Cambridge, 2006.
Eine mögliche Lösung für die rechts formulierte Anschlussaufgabe findet sich hier (als pdf).
Eine andere Herleitung für n = 2:

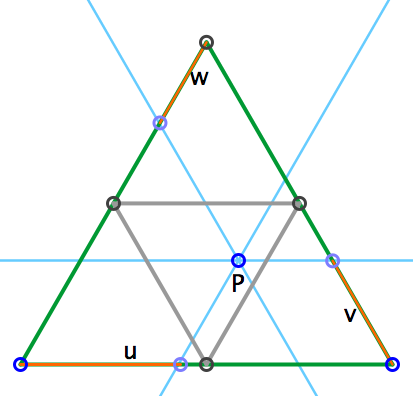
Wir betrachten das gleichseitige Dreieck mit Seitenlänge 1. Für jeden Punkt im Innern dieses Dreiecks gilt - geometrisch sofort ersichtlich -
u + v + w = 1.
Wir fassen u, v und w als die drei Bruchstücke unserer zerbrochenenen Einheitsstrecke auf (die Gesamtlänge ist immer 1): Jede Lage von P erzeugt ein Zerbrechen des Einheitsstabes in 3 Bruchstücke mit Summe 1. Die Bedingung, dass alle Bruchstücke <1/2 sein müssen, wird durch die Lagen von P innerhalb des grauen kleinen Dreiecks im Bild rechts angegeben. Dessen Fläche ist 1/4 der Gesamtfläche des grossen Dreiecks. Damit haben wir erneut p = 1/4 gefunden.
Die in der angegebenen Quelle hergeleitete Formel für beliebige n lautet:
p("konvexes Polygon möglich") = 1 - (n + 1)/2n .
Für n = 2 (Dreieck) ergibt sich unser Wert 1/4, für n = 3 (Viereck) der Wert 1/2.
Anschlussaufgabe: Man suche eine Herleitung, die leichter auf beliebige n zu verallgemeinern ist, als unsere speziell auf n = 2 zugeschnittene geometrische Herleitung.
34. Sei n = Anzahl Schülerinnen und Schüler, a = Anzahl Personen des einen Geschlechts,
b = n - a = Anzahl Personen des andern Geschlechts. Sei a > b.
Lösungsweg 1: Baum zeichnen (s. Spalte rechts)
Lösungsweg 2:
Anzahl günstige Paare (gemischt): ab = a(n - a)
Anzahl mögliche Paare: n (n - 1) / 2.
=> a(n - a) : [n(n - 1)/2] = 1/2 =>
4a2 - 4an + n2 - n = 0.
Wir lösen diese quadratische Gleichung nach a auf und finden (a ist der grössere Anteil; wir wählen also die grössere der beiden Lösungen - die andere ist b):
a = (n + √n) / 2 und b = (n - √n) / 2.
Da a und b ganzzahlig sein müssen, muss n eine Quadratzahl sein. Die ersten Lösungen sehen so aus:
| n | 0 | 1 | 4 | 9 | 16 | 25 | 36 | ... |
| a | 0 | 1 | 3 | 6 | 10 | 15 | 21 | ... Dreieckszahlen |
| b | 0 | 0 | 1 | 3 | 6 | 10 | 15 | ... Dreieckszahlen (1 Stufe verschoben) |
Wir finden:
a und b sind aufeinanderfolgende Dreieckszahlen und n = a + b.

Baum zu Lösungsweg 1: Die Pfadregeln führen auf dieselbe quadratische Gleichung wie Lösungsweg 2.
Aufgabe (leicht modifiziert) aus Dierk Schleicher, Malte Lackmann: Eine Einladung in die Mathematik, Springer Spektrum, Heidelberg 2013.
35.
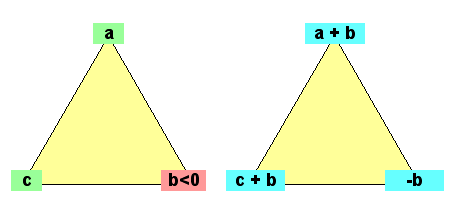
Versuch 1: Eine naheliegende Idee wäre, als Funktion s = |a|+|b|+|c| zu betrachten. Wie man rasch feststellt, gibt es jedoch Fälle, in denen diese Funktion von Schritt zu Schritt nicht abnimmt.
Wie sähe diese Funktion nach einem Schritt aus? Es ergäbe sich:
|a+b|+|b|+|b+c|.
Es treten somit neue Terme auf, nämlich Summen benachbarter Zahlen. Man kann nun versuchsweise solche Summen benachbarter Zahlen in die gesuchte Funktion einbauen:
Versuch 2: s = |a|+|b|+|c|+|a+b|+|b+c|+|c+a|. Diese Funktion ist symmetrisch (invariant) in Bezug auf zyklische Vertauschung von a, b und c (das muss sie auch sein). Wie sieht nun die Funktion nach einem Schritt aus? Es ergibt sich:
|a+b|+|b|+|b+c|+|a|+|c|+|a+2b+c|. Die Funktion wird langsam "selbstgenügsam"; viel wesentlich Neues kommt in einem Iterationsschritt nicht mehr dazu.
Es ist nun tatsächlich
|a|+|b|+|c|+|a+b|+|b+c|+|c+a| > |a+b|+|b|+|b+c|+|a|+|c|+|a+2b+c|
oder gleichbedeutend
|a+c| > |a+2b+c|,
denn (a+c) ist positiv (weil b negativ ist, a+b+c jedoch positiv sein muss); daraus folgt obige Behauptung.
Die gesuchte Funktion lautet somit:
s = |a| + |b| + |c| + |a+b| + |b+c| + |c+a|.
Diese Funktion nimmt von Schritt zu Schritt echt ab, und folglich endet das Verfahren einmal. (Es sind noch andere Funktionen möglich, die denselben Zweck erfüllen.)
Nun kann eine Verallgemeinerung auf Vier- und Fünfecke vermutet werden...
Bemerkung zum Lösen mathematischer Probleme
In obigem Lösungsansatz kommen folgende Arbeitstechniken zum Zug:
- "Verkleinern" des Problems. Anstelle eines Fünfecks wird lediglich ein Dreieck betrachtet.
- Suchen einer Funktion, welche jeder Konfiguaration eine natürliche "Kennzahl" zuordnet. Das Betrachten dieser Kennzahl ist einfacher als das Betrachten der Zahlkonfigurationen. Eine Lösung gelingt allein durch Kenntnis solcher Kennzahlen. Man projiziert das ursprüngliche Problem mittels einer Funktion in die einfache Struktur der natürlichen Zahlen.
- Symmetriebetrachtungen: Die Funktion, die jeder Konfiguration eine natürliche Zahl zuordnet, muss unter zyklischer Vertauschung von a, b, c unverändert bleiben, denn anstelle von b könnten auch c oder a negative Zahlen sein.
Es darf bezweifelt werden, ob ein noch so hoch entwickelter Supercomputer je in der Lage sein wird, beispielsweise solche Hilfsfunktionen oder andere nützliche Lösungswerkzeuge zu suchen. Dazu ist eine ganze Erfahrungs-Biografie nötig. Oft entstehen kreative und neue Lösungen durch Erfahrungen, die man in ganz verschiedenen Gebieten der Mathematik gesammelt hat. In loser Assoziation tauchen mögliche Werkzeug-Ideen auf, die man früher einmal erfolgreich angewendet hat. Es gibt in diesem Stadium noch keine formale Begründung für die Wahl und das Ausprobieren eines solchen Werkzeugs. Falls das Werkzeug erfolgreich ist, entsteht die formale Begründung hinterher. Es gab keine vorprogrammierte Intuition, vielmehr findet ein bildhaftes, suchendes Herumkramen in der eigenen Biografie bisheriger Problemlösungen statt. Oft braucht es -wie der Mathematiker Henri Poincaré es beschreibt- dazu auch noch ein paar Tassen starken Kaffee und den überreizten Zustand einer durchgearbeiteten Nacht...
36.

Wir betrachten den Zahlenstrahl, wenden jedoch einen Trick an: Wir schliessen das Stück [0 ; 1] des
Zahlenstrahls zu einem Kreis mit Umfang 1.
Nun starten wir bei 0 und tragen im Gegenuhrzeigersinn laufend log(7) ab. Jedes Mal, wenn wir beim
roten Punkt (s. Abb.) vorbeikommen, zählt uns ein "Zähler" eine Runde dazu.

Da lg(7) irrational ist, entstehen beim fortwährenden Addieren von lg(7) stets neue Punkte. Es "regnet" also fortwährend neue Punkte in die Kreislinie hinein. Dieser Punktregen wird immer dichter.
Zu zeigen wäre noch, dass der Punktregen sich "gut" über die Kreislinie verteilt, dass insbesondere keine Dauerlücke um den roten Punkt herum offen bleibt. Wie liesse sich dies plausibel erklären? *)
Unter dieser Voraussetzung wird nun der Punktregen um den roten Punkt herum beliebig dicht und man findet einen Punkt n⋅lg(7), der ein beliebig kurzes Kreisbogenstück oberhalb des roten Punktes liegt.
Damit ist gezeigt, dass es zu jedem noch so hohen m ∈ ℕ Siebnerpotenzen mit mindestens m aufeinander folgenden Nullen in der Dezimaldarstellung gibt.
Allerdings ist damit noch nicht gezeigt, dass es zu jedem m Siebnerpotenzen mit genau m aufeinander folgenden Nullen in der Dezimaldarstellung gibt.
Man kann jedoch aus einer Siebnerpotenz der Dezimalform 1 0...0 ∗∗∗ durch Multiplikation mit 7 oder mit 72 eine neue Siebnerpotenz mit weniger Nullen in Folge erzeugen,
z.B. aus
7510 = 1.0000009...⋅10431 (6 Nullen in Folge) die Zahl
7511 = 7.000006...
⋅10431 (5 Nullen in Folge) und mittels erneuter Multiplikation mit 7 die Zahl
7512 = 4.900004... 10432 (4 Nullen in Folge).
Bemerkung: Wann ist ein Problem gelöst? Unser Beweis ist ein reiner Existenzbeweis. Er gibt keine konkrete Zahl an. Wir haben eine wichtige Arbeitstechnik verwendet: Anstelle des unendlichen Zahlenstrahls betrachteten wir eine geschlossene Kreislinie. Dadurch verlief sich der "Punkte-Regen" nicht ins Unendliche, sondern wurde auf der begrenzten Kreislinie immer dichter.
Gibt es "konkretere" Lösungen dieses Problems?
*) 6⋅log(7) überschreitet den roten Punkt um ca. 0.07... Solche "Sechserschritte" rastern somit den Kreis bereits recht eng. Der Punkt nach 15 solcher Sechserschritte, also 90⋅log(7) überschreitet den roten Punkt um 0.05...< 0.07... Diese Neunzigerschritte erzeugen somit einen noch engeren Raster und lassen schliesslich einen Punkt entstehen, dessen Abstand zum roten Punkt noch kleiner wird als 0.05..., z.B. 17⋅90⋅log(7) = 1530⋅log(7). Dieser Punkt überschreitet den roten Punkt um nur noch 0.000001... . Auf diese Weise entstehen immer dichtere Raster und Punkte, die vom roten Punkt beliebig kleinen Abstand haben.
Das Beispiel unten zeigt, dass jedoch bereits 510⋅log(7) einen sehr, sehr eng am roten Punkt anliegenden Punkt liefert: Sein Abstand beträgt noch 0.0000004....
Gibt es ev. einen Algorithmus, der systematischer vorgeht als der hier skizzierte Gedankengang?
Obiger Beweis ist sehr unkonkret.
Das Durchprobieren von n⋅ lg(7) mittels eines Computerprogramms zeigt:
510⋅ lg(7) = 431.0000004... .
W
ir betrachten somit 7510. Rechts das Resultat mit seinen 432 Ziffern. Man sieht, dass 6 Ziffern 0 in Folge auftreten.
Man braucht unheimlich riesige Potenzen, um die Punktdichte auch nur wenig anwachsen zu lassen. So ist z.B.
1'878'356'265⋅lg(7) = 1'587'395'198.0000000073...
Die riesige Zahl 71'878'356'265 ergäbe also eine Zahl, die 7 Nullen in Folge enthielte
(100.0000000073...≈ 1.000000017...).
Der oben geführte Existenzbeweis kommt also ziemlich nonchalant daher. Er kümmert sich überhaupt nicht um praktisch-algorithmische Schwierigkeiten. Hier, im Bereich der Numerik und der Algorithmen, würde es dann erst richtig knifflig.

In obiger Aufgabe zeigen sich auch die Grenzen der intuitionistischen oder konstruktivistischen Mathematik, welche nur Beweise zulässt, die konstruierbar sind. Das Vorgehen oben ist ja eine Konstruktionsanleitung für die Herstellung der geforderten Siebnerpotenzen. Trotzdem wird für hohe Werte von m jeder auch noch so leistungsfähige Rechner versagen, da unglaublich hohe Zahlen entstehen. Selbst wenn es dereinst immer noch bessere Rechner geben wird, kommen diese bei noch höheren m-Werten erneut an ihre Grenzen.
Sei x(k) die Anzahl Möglichkeiten, k Treppenstufen mittels der erlaubten Stufenschritte (hier zunächst 1- oder 2-Stufenschritte) zu ersteigen.
8 Treppenstufen in 1- oder 2-Stufenschritten ersteigen:
Sei x(8) die Anzahl Möglichkeiten dafür.
Wir können 2 Fälle unterscheiden:
-Fall 1: Der letzte Schritt ist ein Einerschritt. Das führt zu gleich vielen Möglichkeiten wie x(7).
-Fall 2: Der letzte Schritt ist ein Zweierschritt. Das führt zu gleich vielen Möglichkeiten wie x(6).
Es ist also x(8) = x(6) + x(7).
Wir können also das Problem stufenseise aufbauen:
x(1): Treppe mit 1 Stufe: 1 Möglichkeit; x(1) = 1
x(2): Treppe mit 2 Stufen: 2 Möglichkeiten; x(2) = 2
x(3) = x(1) + x(2) = 1 + 2 = 3
x(4) = x(2) + x(3) = 2 + 3 = 5
usw.
Es entsteht die bekannte Fibonacci-Folge:
1 2 3 5 8 13 21 34 55
Mit 8 Stufen ergeben sich somit 34 Möglichkeiten, diese mit Einer- oder Zweierschritten zu ersteigen.
8 Treppenstufen in 1- oder 2- oder 3-Stufenschritten ersteigen:
Die Verallgemeinerung auf 1- oder 2- oder 3-Stufenschritte liegt auf der Hand: Um das neue Glied der Zahlfolge zu erhalten, müssen wir die drei Vorgängerglieder addieren:
x(1) = 1
x(2) = 2
x(3) = 4
x(4) = 1 + 2 + 4 = 7
x(5) = 2 + 4 + 7 = 13, usw.
Es entsteht die Folge der Tribonacci-Zahlen(vgl. Online Encyclopedia of integer sequences)
1 2 4 7 13 24 44 81 ...
Es gibt also 81 Möglichkeiten, 8 Stufen in Einer- oder Zweier- oder Dreierschritten zu bewältigen.
Anzahl Möglichkeiten, wenn 1- bis 7-Stufenschritte erlaubt sind?
1 2 4 8 16 32 64 127 253 ... (Heptanacci-Zahlen).
Folgefrage:
Besteht der Anfang der Folge immer aus Zweierpotenzen? Die Antwort ist ja (siehe Problem 38).
Anzahl Möglichkeiten, wenn 1- bis k-Stufenschritte erlaubt sind?
Es entsteht die Folge der "k-bonacci-Zahlen". Die Folge kann so aufgebaut werden:
-Zuerst setzt man k Nullen, anschliessend eine 1.
-Des Weiteren ergibt sich das nächste Glied immer aus der Summe der k Vorgängerglieder.
Beispiel k = 7:
0 0 0 0 0 0 0 1 1 2 4 8 16 32 64 127 253 ...
Man sieht, dass anfänglich die Zweierpotenzen entstehen: 1 2 4 8 ... 64.
38. Summenzerlegungen einer natürlichen Zahl
- Auf wie viele Arten kann ich eine 7-stufige Treppe in 1-, 2-, ..., oder 7-Stufenschritten ersteigen? Allgemein: eine m-stufige Treppe in Schritten der Weite 1 oder 2 oder ... oder m?
- Auf wie viele Arten kann ich zwischen m Spielsteine Trennstäbe einbauen (max. 1 Trennstab zwischen zwei benachbarte Steine)?
- Auf wie viele Arten kann ich die natürliche Zahl m in Summanden zerlegen?
Beispiel: 5 = 1 + 1 + 1 + 1 + 1 = 1 + 1 + 3 = 1 + 3 + 1 = ...
(1 + 1 + 3 und 1 + 3 + 1 sollen hier als verschiedene Arten gelten. Man beachte im Gegensatz hierzu die Zusatzaufgabe 38a, in welcher diese Varianten identifiziert werden. Dadurch entsteht ein äusserst vertracktes Problem, das elementar nicht zu lösen ist.)
Alle 3 Probleme sind gleichwertig, d.h. haben dieselbe Lösung.
Am einfachsten ist wohl das Legen von Trennstäben:
m Steine haben m - 1 Lücken. Bei jeder Lücke habe ich 2 Möglichkeiten: Trennstab legen oder Trennstab nicht legen.
Das ergibt total 2m -1 Möglichkeiten.
So kann ich die Zahl 5 auf 24 = 16 Arten in Summanden zerlegen.
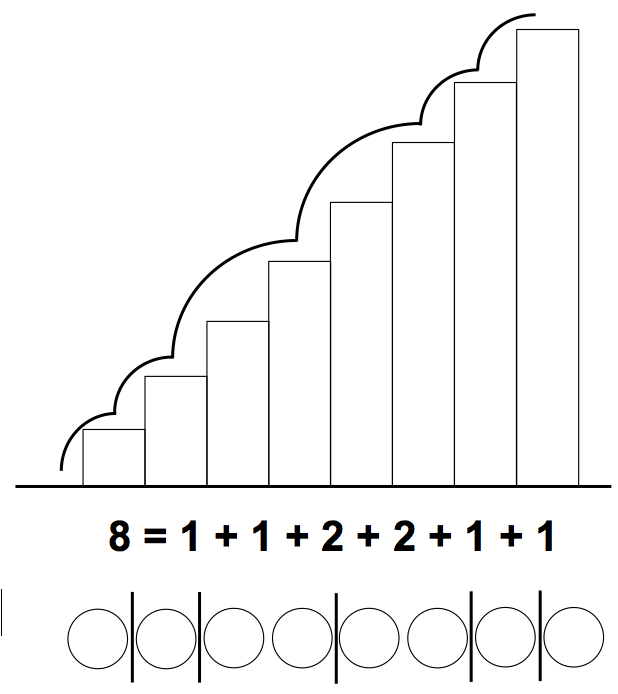
Ersteigen einer 8-stufigen Treppe in lauter Einer- oder Zweierschriten bzw. Legen von Trennstäben zwischen Spielsteine.
Die Summenzerlegungen der 4. Gleichfarbig die miteinander identifizierten Varianten:
4
3+1
2+2
2+1+1
1+3
1+2+1
1+1+2
1+1+1+1
Es verbleiben 5 Partitionen der 4 (schwarz, blau, grün, rot, lila).
Die Werte für die Anzahl Partitionen steigen rasant an. Für die Zahl 100 gibt es über 190 Millionen Partitionen, für die Zahl 200 fast 4 Billionen.
a) Zur Zahl 5 existieren 7 Partitionen.
b) Zur Zahl 9 gibt es 7 Partitionen mit genau 3 Summanden. Man findet sie am besten durch "lexikografisches Vorgehen": 1+1+7, 1+2+6, 1+3+5, 1+4+4, 2+2+5, 2+3+4, 3+3+3.
c) Zur Zahl 9 gibt es 6 Partitionen mit genau 4 Summanden: 1+1+1+6, 1+1+2+5, 1+1+3+4, 1+2+2+4, 1+2+3+3, 2+2+2+3.
Die Zahlfolge der Partitionen erfüllt offenbar das Benfordsche Gesetz. Hier eine Tabelle der Anfangsziffern-Häufigkeit unter den ersten 50 Folgenzahlen und zum Vergleich die theoretischen Benford-Zahlen lg[(x+1)/x]. Betrachtet man längere Folgenstücke, werden die Benford-Zahlen zunehmend genauer erreicht.
| Anfangsziffer | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Auftretens-Häufigkeit der Anfangsziffer in % | 38 | 14 | 14 | 8 | 8 | 6 | 8 | 4 | 0 |
| Theoretische Häufigkeit nach Benford-Gesetz in % | 30.1 | 17.6 | 12.5 | 9.7 | 7.9 | 6.7 | 5.8 | 5.1 | 4.6 |
x3 - y3 = 91. Wir setzen: x - y =: d. Somit ist x = y + d und
x3 - y3 = (y + d )3 - y3 = y3 + 3y2d + 3yd2 + d3 - y3 =
3y2d + 3yd2 + d3 = d(3y2 + 3yd + d2) = 7 * 13 = 13 * 7 = 1 * 91 = 91 * 1
Wegen y > 0 muss d < 4 sein, sonst würde 3y2d + 3yd2 + d3 > 91. Von obigen Zerlegung bleibt also einzig 1 * 91, d.h. d = 1 und 3y2 + 3yd + d2 = 91, d.h.
3y2 + 3y + 1 = 91 oder 3y2 + 3y - 90 = 0 und somit y = 5 und x = 6.
Somit lautet die einzige Lösung mit natürlichen Zahlen (6 / 5) oder 63 - 53 = 91.
Alternativlösung:
x3 - y3 = (x - y)(x2 + xy + y2) = 91
Es ist sicher x ≤ 7, denn 73 - 63 = 127 > 91. Dann ist x - y ≤ 6.
Dann bleibt für (x - y) als Teiler von 91 nur 1, d.h. x - y = 1 oder y = x - 1
Es folgt: x2 + xy + y2 = x2 + x(x - 1)+ (x - 1)2 = 3x2 - 3x + 1 = 91
oder 3x2 - 3x - 90 = 0 => x = 6 => y = 5
x(n+2) = x(n) + x(n+1). Sei x der Grenzwert der Quotientenfolge
x(n+1) / x(n). Je grösser n ist, desto besser nähert sich dieser Quotient dem Grenzwert x an. Sehr, sehr weit hinten in der Fibonacci-Folge gilt also näherungsweise:
x(n+1) = x * x(n) und x(n+2) = x2 * x(n), somit
x(n+2) = x(n) + x(n+1) oder x2 * x(n) = x(n) + x * x(n). Division durch x(n) ergibt
x2 = 1 + x oder x2 - x - 1 = 0. x = (√5 + 1) / 2.
Die Verallgemeinerung liegt auf der Hand:
Tribonacci-Folge:
Die Quotientenfolge konvergiert gegen die Lösung der Gleichung
x3 - x2 - x - 1 = 0, d.h. gegen x = 1.839286755...
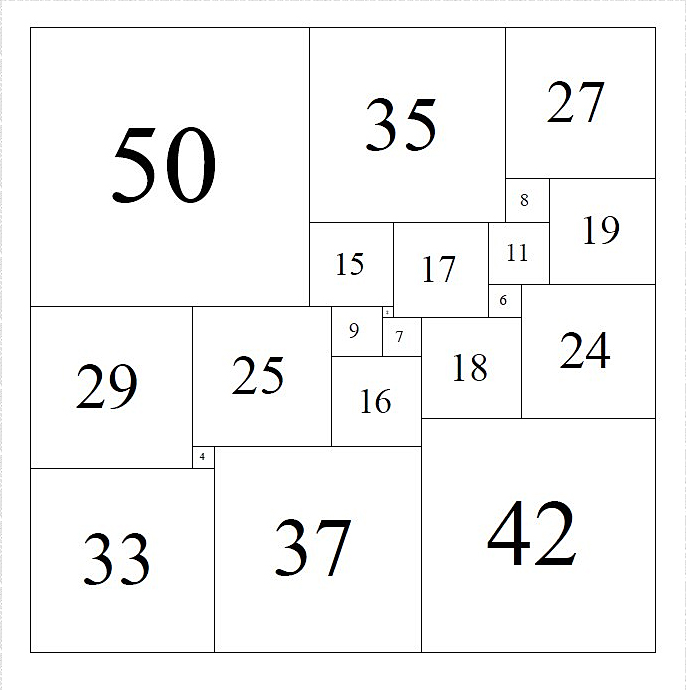
Das kleinste Quadrat hat Seitenlänge 2. Quadrat: 112 x 112.
Zusatz:
Im Quadrat liegt das kleinste Quadrat sicher nicht am Rand des grossen Quadrates (warum?).
Nehmen wir an, wir hätten eine Würfelunterteilung in lauter verschiedene, kleinere Würfel. Auf der Bodenfläche des grossen Würfels entsteht dadurch eine Quadratunterteilung in lauter verschiedene kleinere Quadrate. Das kleinste dieser Quadrate befindet sich im Innern und nicht am Rand. Der Würfel W über diesem Quadrat steht somit im Inneren des grossen Würfels auf einem inneren Quadrat und ist von grösseren Würfeln umgeben.
Auf der oberen Fläche von W befinden sich somit noch kleinere Würfel als W. Wir betrachten nun wieder den kleinsten Würfel, der sich auf der oberen Fläche von W im Inneren dieser oberen Fläche befindet... Der Prozess setzt sich ins Unendliche fort; es entstehen immer kleinere Würfel ohne Ende. Eine endliche Unterteilung ist nicht möglich.
Anmerkung: Was ist Mathematik? - Mathematik enthält auch solche "pittoreske" Beweise jenseits langfädiger formaler Schlussketten. Elegante Überlegungen und "schöne" Beweisfiguren sind genau so Teil der mathematischen Kultur wie formale Ableitungen.
Lösung Rechteck, unterteilt in 9 verschiedene Quadrate:
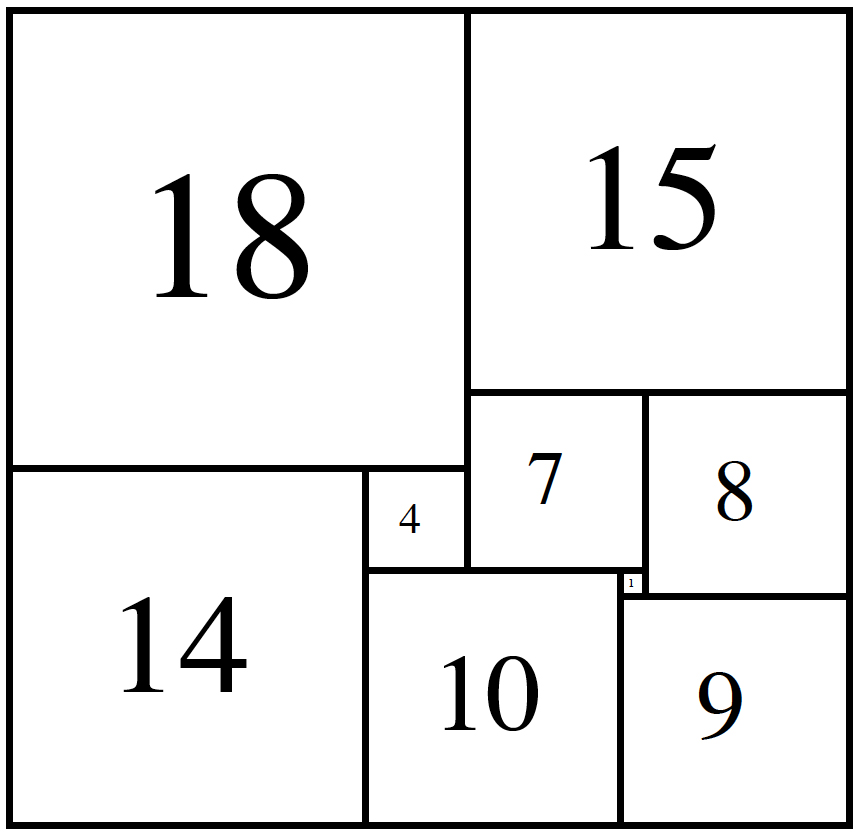
Format: 33 x 32.
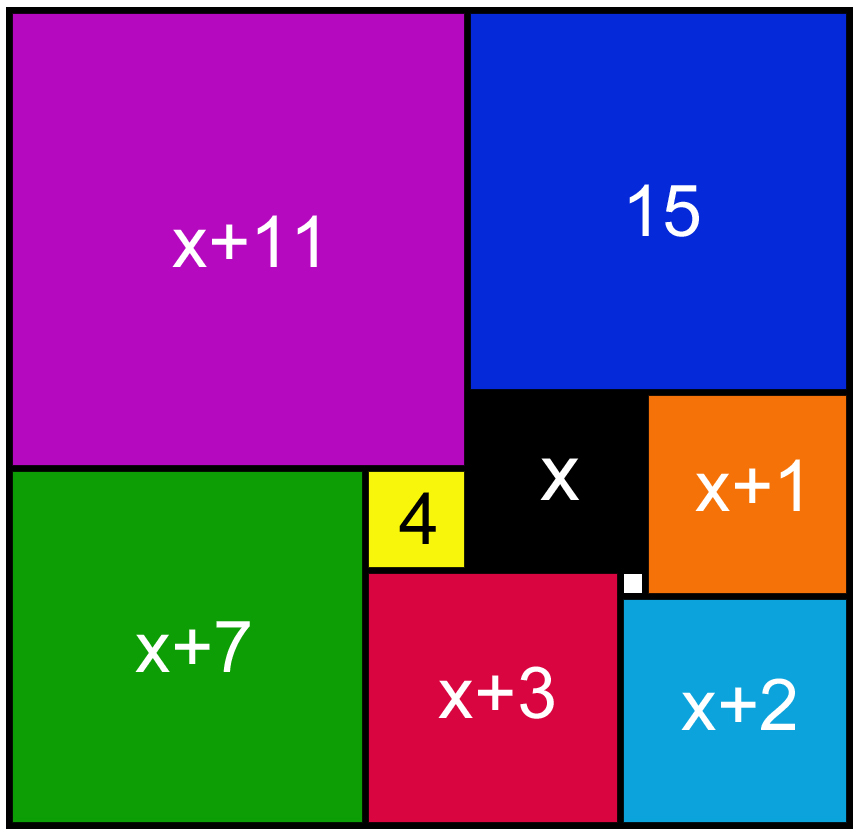
Wir wählen die Seitenlänge des kleinen weissen Quadrates = 1. Sollten sich in der Folge nicht-ganzzahlige Seitenlängen ergeben, multiplizieren wir alle Seitenlängen mit einem geeigneten gemeinsamen Faktor. Das schwarze Quadrat habe Seitenlänge x. Nun lassen sich alle übrigen Quadratseiten durch x ausdrücken (Bild oben).
Es muss nun sein: x + 26 = 3x + 12 (Länge obere Seite = Länge untere Seite). => x = 7 und alle Quadratseiten sind damit bereits ganzzahlig.
Rätsel 1
Beispiel: 33 = 3 + 4 + 5 + 6 + 7 + 8 = s(8) - s(2).
Dabei sei s(i) die Summe der natürlichen Zahlen von 1 bis i.
s(i) = i (i +1) /2.
Zahlen, die als fortlaufende Summe natürlicher Zahlen dargestellt werden können, haben somit die Form n = s(j) - s(i), j > i.
=> 2n = j (j+ 1) - i (i + 1) = j2- i2 + j - i
= (j + i)(j - i) + (j - i) = (j - i)(j + i + 1) = 2n.
Die Differenz der beiden Faktoren links beträgt 2i + 1, ist also ungerade, d.h. die beiden Faktoren haben verschiedene Parität, d.h. einer der Faktoren ist sicher ungerade. Das bedeutet, dass n sicher einen ungeraden Faktor enthalten muss.
Die Zahlen, die nicht als fortlaufende Summe natürlicher Zahlen dargestellt werden können (mit Ausnahme der trivialen Darstellung n = n), dürfen somit keinen ungeraden Faktor enthalten, sind also Zweierpotenzen.
Umgekehrt:
Sobald eine Zahl n einen ungeraden Faktor u ≠ 1 enthält, lässt sie sich als fortlaufende Summe natürlicher Zahlen schreiben.
Konstruktionsanleitung:
Beispiel: 45 = 3⋅15. 15 = 7 + 8.
An diesen Kern setzen wir links und rechts je (3-1)-mal ganze Zahlen an (gleichfarbige Zahlen ergeben Summe 15):
45 = 3 ⋅ 15 = 5 + 6 + (7 + 8) + 9 + 10.
Dieses Vorgehen ist allgemein möglich, sobald ein ungerader Teiler ≠1 vorhanden ist. Somit sind es genau die Zweierpotenzen, die eine solche Darstellung nicht zulassen (mit Ausnahme der trivialen Darstellung n = n).
Weitere Möglichkeit der Zerlegung von 45: 45 = 5⋅9. 9 = 4 + 5.
45 = 0 + 1 + 2 + 3 + (4 + 5) + 6 + 7 + 8 + 9 = 1 + 2 + 3 + (4 + 5) + 6 + 7 + 8 + 9
Noch eine Möglichkeit:
45 = 9⋅5. 5 = 2 + 3 als Kern:
45 = (-6) + (-5) + (-4) + (-3) + (-2) + (-1) + 0 + 1 + (2 + 3) + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11
= 7 + 8 + 9 + 10 + 11.
Die Negativ-Anteile in der Konstruktion (rot) wurden am Schluss noch eliminiert, um eine Darstellung mit natürlichen Zahlen zu erhalten.
Jeder ungerade Teiler kann in dieser Konstruktion als "Mittelkern" dienen; es gibt für ungerade Zahlen n genau so viele Darstellungen von n in fortlaufende natürliche Zahlen, wie es verschiedene ungerade echte Teiler von n (inkl. Teiler 1) gibt. Den Teiler n selber lassen wir weg, da er lediglich die triviale Darstellung n = n erzeugt.
Für gerade Zahlen n mit k ungeraden Teilern (inkl. 1) ergibt Teiler 1 keine Darstellung; wir erhalten dann für gerade Zahlen k - 1 Darstellungen.
Beispiel: 6 = 0 + (1 + 2) + 3.
Beispiel 45: Die echten Teiler von 45 sind 1, 3, 5, 9, 15. Dies liefert 5 nicht-triviale Darstellungen:
| 1⋅45 | 45 = (22+23) |
| 3⋅15 | 45 = 5+6+(7+8)+9+10 |
| 5⋅ 9 | 45 = 0+1+2+3+(4+5)+6+7+8+9 |
| 9⋅ 5 | 45 = (-6)+(-5)+...+0+1+(2+3)+4+5+6+7+8+9+10+11 = 7+8+9+10+11 |
| 15⋅ 3 | 45 = (-13)+(-12)+...+(1+2)+3+...+16 = 14+15+16 |
Zusatzaufgabe:
Es ist 2021 = 43⋅47. Es gibt 3 ungerade echte Teiler: 1, 43 und 47, somit, da 2021 ungerade ist, drei Möglichkeiten:
2021 = -25 + ... + 23 + 24 + ... + 68 = 26 + ... + 68 (43 Summanden). 2021 = 43⋅94/2 *
2021 = -19 + ... + 21 + 22 + ... + 66 = 20 + ... + 66 (47 Summanden). 2021 = 47⋅86/2 *
2021 =
1010 + 1011 (2 Summanden). 2021= 2⋅2021/2 *
*) Notiert man die Summe doppelt wie folgt:
26 + ... + 68
68 + ... + 26
---------------
94 + ... + 94
= 43⋅94, so ergibt die einfache Summe 43⋅94/2 = 43⋅47 = 2021.
Rätsel 2
Das kgV der Teiler von n (ohne n selber) ist gleich n, wenn es eine nicht-triviale Zerlegung n = ab gibt mit ggT(a, b) = 1. Dann ist kgV(a, b) = n, denn es gilt
kgV(a, b) = ab / ggT(a, b) = n / ggT(a, b).
Sobald eine Zahl n in der Primfaktorzerlegung zwei verschiedene Primfaktoren p und q enthält, ist eine solche Zerlegung möglich: n = pr b, r maximal. Es ist dann b≠1, da b noch den Primfaktor q enthält, und pr und b sind teilerfremd.
Dies darf gemäss Aufgabenstellung nicht passieren. n muss deshalb die Potenz eines einzigen Primfaktors p sein. Dies ist auch hinreichend, wie man sofort einsieht.
Beispiel: 27. Echte Teiler: 1, 3, 9. kgV(1, 3, 9) = 9 ≠ 27.
Der Vorgang konvergiert gegen die Lösung 0.739085... der Gleichung
cos(x)=x. (Warum?) Sie haben diese Gleichung durch Iteration gelöst.
Nicht bei jeder Gleichung f(x)=x konvergiert das Verfahren, oder man erhält von mehreren existierenden Lösungen nur eine, egal von welchem Startwert man ausging. Es gibt also Lösungen, die als Attraktoren und solche, die als Repulsoren wirken.
Wer tiefer schürfen will, kann auch diese Phänomene genauer untersuchen.
Bild rechts: Die Iteration grafisch. Das Verfahren konvergiert gegen den Schnittpunkt von y=cos(x) mit y=x; der Schnittpunkt wirkt als Attraktor.
Wie funktioniert diese grafische Iteration? Man beginnt mit einem Startwert ("Start") und geht nach oben zum Graphen der Kosinusfunktion. Indem man von diesem Schnittpunkt aus nach rechts auf die Gerade y=x geht und von dort wieder nach unten zur x-Achse (was man grafisch nicht wirklich auszuführen braucht), macht man diesen Kosinuswert wieder zum neuen x-Eingabewert, von dem man erneut den Kosinuswert abliest, also zum Graphen der Kosinusfunktion hochgeht.
So fährt man weiter: Vom neuen Schnittpunkt zur Geraden y=x und wieder in senkrechter Richtung zum Graphen der Kosinusfunktion, usw.

Das Verfahren terminiert entweder bei der Zahl 1 oder in einer zyklisch durchlaufenen Schleife mit den Zahlen (4; 16; 37; 58; 89; 145; 42; 20). Weitere Schleifen existieren nicht.
Der längste Weg bis zur Endschleife geht von der Zahl 60 oder 6 aus (10 Stufen). Spätestens die 10. Person wird also bei der 1 oder bei der Endschleife landen.
Man kann die 1 ausschliessen und fordern, dass man bei Erreichen der 1 mit einer 2 fortfahren soll. Dann gerät man stets in die unten rot gefärbte Endschleife.


Bild oben (die linke und rechte Bildhälfte ergeben zusammen das ganze Bild): die Bahnen dieses Zahlenspiels.
Hier noch der Hinweis auf die Online Enzyklopädie der ganzzahligen Zahlfolgen oeis.org.
Übrigens: Ein Satz von Fermat besagt, dass sich jede Primzahl, die bei Division durch 4 Rest 1 ergibt als Summe zweier Quadratzahlen darstellen lässt.
Beispiele:
5=22+12; 13=22+32; 17=12+42; 29=22+52; 41=42+52; 53=22+72; usw.
Das obige Strukturbild illustriert dies: Die Primzahlen dieser Form stehen nie am Anfang einer Kette.
Antwort: nein. Für einmal sei die Argumentation physikalisch:
Man denke sich das Vieleck mit einer Dicke ausgestattet, so dass es ein Prisma wird.
Betrachten Sie Lot Nr. 2, das vom Schwerpunkt S senkrecht auf die horizontale momentane Standfläche dieses Prismas verläuft. Aus physikalischen Gründen wird das Prisma kippen; es entstünde eine neue Standfläche.
Träfe jetzt das neue Lot auf die neue Standfläche erneut ausserhalb dieser Standfläche auf, so würde das Prisma erneut kippen. So ginge es immer weiter, wenn jedes Lot ausserhalb der aktuellen Standfläche aufträfe: Der Körper würde von selber dauernd kippen (nach links oder nach rechts) und sich folglich ohne Antrieb stets bewegen: Wir hätten ein Perpetuum mobile, was unmöglich ist.
Folglich existiert ein Vieleck mit der geforderten Eigenschaft nicht.
P.S. In neben stehendem Fünfeck treffen zwei der fünf Lote ausserhalb der zugehörigen Seiten auf. Sind Fünfecke denkbar, bei denen die Anzahl der Lote mit dieser Eigenschaft grösser als 2 ist?


Zwischenzentralitätswerte der einzelnen Punkte:
Nr. 1: 0
Nr. 2: 0
Nr. 3: 9.333...
Nr. 4: 1
Nr. 5: 0.333...
Nr. 6: 1
Nr. 7: 1.333...
Hier nochmals Cantors Definition für die Höhe N eines Polynoms vom Grad n mit Koeffizienten aus ℤ:
N = (Summe der Absolutbeträge der Koeffizienten) + n - 1.
Aufgabe 1:

N=4: 12 Polynome mit natürlichen und 44 Polynome mit ganzen Koeffizienten.
Aufgabe 2:
Wäre die Höhe N lediglich als Grad n des Polynoms definiert, gäbe es unendlich viele Koeffizienten-Möglichkeiten (die würden ja gar nicht in die Berechnung von N einfliessen) und es gäbe somit unendlich viele Polynome mit dieser "Höhe".
Wäre die Summe der Absolutbeträge der Koeffizienten allein für die Höhe N verantwortlich, so könnte der Grad und damit die Anzahl Nullstellen beliebig hoch sein.
Cantors Definition beschränkt die Möglichkeiten für die Koeffizienten UND für den Grad (der höchstens gleich N sein kann). Damit wird erst eine Auflistung möglich, wie wir sie am Beispiel N = 4 in der linken Spalte ausgeführt haben.
Auflistung für N = 4: Man bringe die 44 Polynome links in eine Reihenfolge. Anschliessend bringe man innerhalb jedes Polynoms dessen Nullstellen in eine Reihenfolge. Somit hat man für N = 4 die algebraischen Zahlen "aufgezählt". So verfährt man für jede Wahl von N; die N-Werte werden ebenfalls aufsteigend geordnet. Damit entsteht eine Aufzählung aller algebraischer Zahlen.

Anmerkung:
Die links unter d) definierte Abbildung h ist eine Bijektion h: ℝ⁺ → [0 ; 1].
Eine Bijektion f: ℝ → (-1 ; 1) lässt sich elementargeometrisch, also ohne CBS-Satz, wie folgt finden:

Der reellen Zahl r auf der x-Achse wird via die Punkte R und S (grüne Pfeile) der Punkt r' im Intervall (-1 ; 1) bijektiv zugeordnet.
Die Formeln ergeben sich direkt via Ähnlichkeit und lauten:

Zuordnung f: ℝ → (-1 ; 1) als Graph:

Statt also ganz ℝ zu studieren, kann man häufig lediglich die "Nullkomma-Zahlen" im Intervall
(-1 ; 1) betrachten.
Seien 10a+b und 10c+d zwei Zahlen, welche die Denksport-Bedingung
| (10a+b)(10c+d)=(10b+a)(10d+c) |
erfüllen; a, b, c, d ∈ {1,2,3,4,5,6,7,8,9}.
(Die Null entfällt, da wir uns auf echte zweistellige Zahlen beschränken; damit entfallen auch alle Zehnerzahlen, deren Spiegelzahlen einstellig wären.)
Beispiel: 36 und 42 (a=3, b=6, c=4, d=2): Es gilt: 36⋅42=63⋅24.
Ausmultiplizieren und Kürzen der Gleichung (10a+b)(10c+d)=(10b+a)(10d+c) zeigt,
| dass die Denksportbedingung genau dann gilt, wenn a⋅c=b⋅d oder, äquivalent, a:b=d:c ist. |
Das bedeutet zum Beispiel, dass zu 12 als Partnerzahl noch genau 21, 42, 63 und 84 in Frage kommen (d:c=1:2).
12 selber kann aber auch noch durch die Zahlen 24, 36 und 48 ersetzt werden, welche dasselbe Ziffernverhältnis 1:2 haben wie 12. Dies führt dann wieder zu einer korrekten Gleichung.
Beispiel: 36⋅42 = 63⋅24 erfüllt immer noch a:b=d:c und somit die Denksportbedingung.
Zur Zahl 12 gibt es also folgende Möglichkeiten: Wir haben eine linke Schublade L von möglichen Ausgangszahlen (a:b=1:2) und eine rechte Schublade R von dazu möglichen Partnerzahlen (d:c=1:2 oder, äquivalent, c:d=2:1):
L = {12, 24, 36, 48}, R = {21, 42, 63, 84}. (R besteht aus den Spiegelzahlen von L.)
Man entnehme eine Zahl aus L und eine aus R. Dies ergibt eine Gleichung, welche die Denksportbedingung erfüllt: Beispiel: 36⋅84 = 63⋅48; a:b=d:c ist erfüllt.
Triviale Gleichungen
Es gibt 45 triviale Schnapszahlgleichungen der Art 11⋅22=11⋅22 oder 55⋅66=55⋅66, usw.
Dann gibt es 36 ebenfalls triviale Gleichungen der Art
12⋅21=21⋅12 oder 15⋅51=51⋅15, bei denen völlig klar ist, dass die Ziffernumkehr dasselbe Produkt liefert.
Beispiel: Zur Zahl 15 existiert kein Vielfaches mit Ziffernverhältnis a:b=1:5 (1:5 ist wegen der 5 im einstelligen Bereich nicht erweiterbar); wir haben L={15}, R={51}. Diese einelementigen Schubladen genieren lediglich die triviale Gleichung
15⋅51=51⋅15.
Nicht-triviale Lösungen gibt es nur, wenn wir die Schnapszahlen weglassen und wenn die oben erwähnten Mengen L und R mehr als ein Element enthalten.
Es bleiben 14 nicht-triviale Gleichungen:
Es bleiben folgende zweistellige Zahlen, die nicht-triviale Gleichungen liefern können (alle Ziffern müssen ≤ 4 sein, damit die Ziffernverhältnisse a:b im einstelligen Bereich erweiterbar sind und so die Mengen L und R mindestens 2 Elemente haben):
12, 13, 14, (21), 23, 24, (31), (32), 34, (41), (42), (43). Die eingeklammerten Zahlen sind die Umkehrzahlen von bereits aufgezählten Zahlen und kommen in die R-Schublade. Zu den Zahlen der Liste fügen wir noch die Vielfachen hinzu, die bei schriftlicher Multiplikation keine Überträge generieren (mithin dasselbe Ziffernverhältnis haben) und verstauen diese 28 Zahlen in folgende L-R-Schubladen, die nun alle zwei oder mehr Elemente haben:
| L = {12, 24, 36, 48} und R = {21, 42, 63, 84} | generiert 6 nicht-triviale Gleichungen |
| L = {13, 26, 39} und R = {31, 62, 93} | generiert 3 nicht-triviale Gleichungen |
| L = {14, 28} und R = {41, 82} | generiert 1 nicht-triviale Gleichung |
| L = {23, 46, 69} und R = {32, 64, 96} | generiert 3 nicht-triviale Gleichungen |
| L = {34, 68} und R = {43, 86} | generiert 1 nicht-triviale Gleichung |
Haben L und R je n Elemente, so ergeben sich n⋅(n-1)/2 nicht-triviale Gleichungen.
Es entstehen somit 6 + 3 + 1 + 3 + 1 = 14 nicht-triviale Gleichungen.
Die Formel n⋅(n-1)/2 sei am Beispiel L = {13, 26, 39} und R = {31, 62, 93} erläutert:
13⋅62 = 31⋅26; 13⋅93 = 31⋅39; 26⋅93 = 62⋅39. Weitere nicht-triviale Gleichungen sind mit diesem L-R-Vorrat nicht möglich. Wir erhalten 3⋅2/2 = 3 nicht-triviale Gleichungen.
Dies sind die 14 nicht-trivialen Gleichungen:
| 12⋅42=21⋅24 | 12⋅63=21⋅36 | 12⋅84=21⋅48 | 24⋅63=42⋅35 | 24⋅84=42⋅48 | 36⋅84=63⋅48 |
| 13⋅62=31⋅26 | 13⋅93=31⋅39 | 26⋅93=62⋅39 | |||
| 14⋅82=41⋅28 | |||||
| 23⋅64=32⋅46 | 23⋅96=32⋅69 | 46⋅96=64⋅69 | |||
| 34⋅86=43⋅68 |
(Erneut verifiziert man überall a⋅c = b⋅d oder äquivalent a : b = d : c)
Die Menge M = {1, 2, ... , 2n} enthält n gerade und n ungerade Zahlen.
Beispiel: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} enthält 5 gerade und 5 ungerade Zahlen.
Wir wählen n+1 Zahlen aus M aus. Somit enthält jede Auswahl mindestens eine gerade und eine ungerade Zahl, d.h. jede Auswahl ist "gemischt".
Wir nehmen nun eine (oder allenfalls die eine) gerade Zahl und dividieren sie so lange durch 2, bis das Ergebnis ungerade wird (ist die gerade Zahl eine Zweierpotenz, wird das Ergebnis schliesslich 1). Wenn das ungerade Ergebnis u in unserer Auswahl liegt, sind wir fertig: Wir haben u und 2ⁱ⋅u in der Auswahl.
Falls u nicht in der Auswahl liegt, muss dafür notwendigerweise eine weitere gerade Zahl in der Auswahl liegen (für jede nicht-vorkommende ungerade Zahl liegt eine gerade Zahl in der Auswahl). MIt dieser verfahren wir gleich. Es entsteht erneut eine ungerade Zahl. Liegt sie in der Auswahl, sind wir fertig, wenn nicht, liegt eine weitere gerade Zahl vor, mit der wir gleich verfahren, usw.
Schliesslich muss eine der entstehenden ungeraden Zahlen in der Auswahl liegen, denn jede Auswahl ist ja "gemischt". Damit sind wir fertig. u und 2ⁱ⋅u liegen in der Auswahl und u teilt 2ⁱ⋅u.
Beispiel: M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. n = 5, n+1 = 6. Wir wählen 6 Zahlen aus M.
Auswahlbeispiel 1 : {1, 2, 4, 6, 8, 10}.
1 teilt jede andere Zahl der Auswahl.
Auswahlbeispiel 2: {2, 3, 5, 6, 8, 9}.
Wir wählen z.B. 8 und teilen fortlaufend durch 2. Es entsteht 1: nicht in der Auswahl. Wir nehmen eine andere gerade Zahl, z.B. 4: Fortlaufendes Teilen durch 2 liefert erneut 1: nicht in der Auswahl. Wir nehmen eine andere gerade Zahl: 6. Fortlaufendes Teilen durch 2 liefert 3: Liegt in der Auswahl: 3 teilt 6.
Sei xi die Wahrscheinlichkeit, dass der erste Würfel die Augenzahl i zeigt.
Sei yj die Wahrscheinlichkeit, dass der zweite Würfel die Augenzahl j zeigt.
Wir vergleichen die "Extreme": Augensumme 2 und Augensumme 12 mit Augensumme 7.
P steht für "Probability":
Es ist
P(Augensumme 2)=P(Augensumme 7)=1/11 und P(Augensumme 12)=P(Augensumme 7)=1/11;
formal:
(1): x1y1 = x6y1 + x5y2 + x4y3 + x3y4 + x2y5 + x1y6 = 1/11; es folgt x1y1 und damit auch x1, y1 > 0
(2): x6y6 = x6y1 + x5y2 + x4y3 + x3y4 + x2y5 + x1y6 = 1/11; es folgt x6y6 und damit auch x6, y6 > 0
Aus (1) und (2) folgt:
(3.1): x1(y1 - y6) = x6y1 + x5y2 + x4y3 + x3y4 + x2y5 und
(3.2): y1(x1 - x6) = x5y2 + x4y3 + x3y4 + x2y5 + x1y6
(4.1): x6(y6 - y1) = x5y2 + x4y3 + x3y4 + x2y5 + x1y6 und
(4.2): y6(x6 - x1) = x6y1 + x5y2 + x4y3 + x3y4 + x2y5
Die rechten Seiten obiger Gleichungen sind > 0, da x6y1 und x1y6 > 0 sind und kein Summand negativ ist.
Folglich sind auch die linken Seiten positiv und es folgt y1 > y6, x1 > x6, aber auch y6 > y1 und x6 > x1, was ein Widerspruch ist.
Eine Programmierung der Würfel so, dass alle Summen gleich wahrscheinlich sind, ist unmöglich.
Die Zahl sei x. Wir lassen schrittweise die neue Zahl entstehen:
- Subtraktion der Einer: x - 6.
- Division durch 10 (damit rücken alle Ziffern 1 Stelle nach rechts): (x - 6) / 10
- Vorne die 6 anhängen: 6⋅10n + (x - 6) ⁄ 10 = neue Zahl. (n ist vorläufig noch unbestimmt.)
Es entsteht die Gleichung 4x = 6⋅10n + (x - 6) ⁄ 10. Multiplikation mit 10 ergibt
40x = 6⋅10n+1 + x - 6 oder 39x = 6⋅(10n+1 - 1) bzw. 13x = 2⋅(10n+1 - 1).
Damit ergibt sich x = 2⋅(10n+1 - 1) ⁄ 13.
13 teilt somit (10n+1 - 1). Dies trifft erstmals zu für n = 5, also für 999'999.
Damit wird x = 2⋅(106 - 1) ⁄ 13 = 153'846.
Probe: 615'384 ist das Vierfache von 153'846.
Eine viel elegantere Lösung wird hier gezeigt:
https://artofproblemsolving.com/wiki/index.php/IMO_Problems_and_Solutions#1962
alte Zahl: endet mit 6, neue Zahl beginnt mit 6: 6......
alte Zahl ist ein Viertel der neuen Zahl, somit neue Zahl (schriftlich) durch 4 teilen:
Neue Zahl : 4 teilen : 6............ :4 = 1........... = alte Zahl => neue Zahl = 61...
Weiter schriftlich teilen:
61.......... :4 = 15......... = alte Zahl => neue Zahl = 615...
Weiter schrifltich teilen: 615.........:4 = 153.......
= alte Zahl => neue Zahl = 6153...
Weiter schriftlich teilen: 6153.......:4 = 1538..... = alte Zahl => neue Zahl = 61539...
Weiter schriftlich teilen: 61538.....:4 =
15384... = alte Zahl => neue Zahl = 615384...
Weiter schriftlich teilen: 615384...:4 = 153846 = alte Zahl, aufgehend.
a) 23 - 1 = 7 ist z.B. durch 7 teilbar. 23 = 8 ergibt bei Division durch 7 Rest 1.
Wir fragen allgemein:
Welche Zweierpotenzen ergeben bei Division durch 7 Rest 1?
| 2er-Potenz | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| Siebnerrest | 1 | 2 | 4 | 1 | 2 | 4 | 1 |
Alle Zweierpotenzen der Form 23n, n ∈ ℕ, ergeben Siebnerrest 1, d.h. die Zahlen
23n - 1 (oder gleichbedeutend 8n - 1) sind durch 7 teilbar.
Damit eine um 1 vermehrte Zahl durch 7 teilbar ist, muss sie Siebnerrest 6 haben (Bsp: 6, 13, 20, usw.).
Eine Zweierpotenz hat jedoch, wie die Tabelle links zeigt, nie Siebnerrest 6.
Es gibt folglich keine Zahl 2n+ 1, n ∈ ℕ, die durch 7 teilbar ist.
Wir erinnern uns an das uralte babylonische Verfahren, um eine Folge sich annähernder Bruchzahlen zu berechnen.
Als Startzahl wählen wir 1.4, also den Anfang der Dezimaldarstellung von Wurzel 2.

Der Startwert ist wichtig. Wir wählten den Bruch mit einstelligem Zähler und Nenner, welcher der Wurzel 2 am nächsten kommt. Ein weiter entfernter Startwert (z.B. 1.5) würde uns den Bruch 99 ⁄ 70 nicht liefern; es entstünde 17 ⁄ 12.
Zum selben Näherungsbruch gelangt übrigens auch die Kettenbruchentwicklung von √2.
Konvergenzverhalten des babylonischen Verfahrens und Abschätzung von 99 ⁄ 70:

Mit jedem Iterationsschritt verdoppelt sich die Anzahl korrekter Stellen.
Der nächste Bruch 19'601 ⁄ 13'860 stimmt bereits auf 8 Nachkommastellen: 1.41421356...
Das babylonische Verfahren konvergiert somit sehr schnell (quadratisch).
Ergänzung: Das Newton-Verfahren zur iterativen Bestimmung von Nullstellen:
Gegeben ist eine zweimal stetig differenzierbare Funktion mit Nullstelle.
Beispiel: x2 - 2 = 0 mit Nullstelle Wurzel 2.
Taschenrechner ermitteln diese Nullstelle iterativ. Newton-Verfahren:
1. Wähle einen Punkt x0. Lege bei f(x0) die Tangente an den Funktionsgraphen; diese hat die Nullstelle x1.
2. Lege bei f(x1) die Tangente an den Funktionsgraphen; diese hat die Nullstelle x2. Fahre so weiter.
Die Punkte xn werden bei günstiger Wahl der Startstelle x0 gegen die Nullstelle der Funktion f konvergieren.
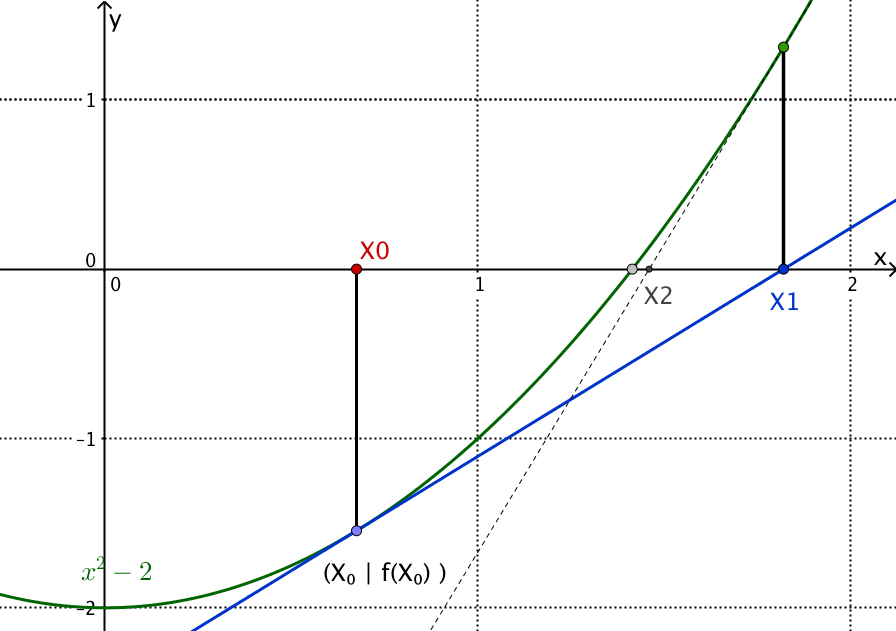
Herleitung der Iterationsformel:

Im Fall der Quadratwurzeln ist das Newton-Verfahren identisch mit dem alten babylonischen Verfahren der Mittelwerte. Der Taschenrechner benötigt nur ganz wenige Iterationsschritte, um die Wurzeln auf hinreichend viele Nachkommastellen genau zu bestimmen.
Die Menge M = {1, 2, ... , n} werde disjunkt aufgeteilt in die Teilmengen S ("Summanden") und F ("Faktoren").
Die Vereinigung von S und F ergibt M.
Die Summe der Elemente von S soll dasselbe ergeben wie das Produkt der Elemente von F.
Sei zunächst n ungerade, d.h. n = 2k+1, k≥2.
Die Summe aller Elemente von M ist n(n+1)/2 = (2k+1)(2k+2)/2 = (2k+1)(k+1) = 2k2+2k+k+1. (*)
Nun bildet man mit 1, k und 2k die Menge F, die übrigen Zahlen bilden die Menge S.
Die Summe der Elemente von S ist deshalb nach (*) gleich 2k2, ebenso das Produkt der Elemente von F.
Diese Konstruktion funktioniert für alle k≥2, d.h. für alle ungeraden Zahlen ≥5.
Beispiel 1:
n = 7, d.h. k = 3: F = {1, 3, 6}, S = {2, 4, 5, 7}. 1⋅3⋅6 = 2+4+5+7 = 18.
Beispiel 2:
n = 99, d.h. k = 49: F = {1, 49, 98}. S = {2, 3, ... , 48, 50, 51, ... , 97, 99}.
Summe bzw. Produkt = 4802.
Der Fall n gerade, d.h. n = 2k, ist weniger einfach zu knacken. Man kommt ihm aber auf die Spur durch Vergleich von n = 7 und n = 6, d.h. beide Male k = 3:
n = 7:
1⋅3⋅6 = 2+4+5+7
n = 6:
1⋅2⋅6 = 3+4+5
Offenbar wird der mittlere Faktor um 1 verringert, was das Gesamtprodukt um 6 kleiner macht:
Auf der Summenseite wird 2 durch 3 ersetzt (Zuwachs 1), jedoch 7 weggelassen (Verringerung 7) , was die Summe insgesamt ebenfalls um 6 verkleinert. Somit bleiben Summe und Produkt wieder gleich.
Dieses Beispiel kann nun leicht allgemein gefasst werden:
n = 2k. n(n+1)/2 = 2k(2k+1)/2 = k(2k+1) = 2k2+k. (*)
Nun bildet man mit 1, (k-1) und 2k die Menge F; der Rest bildet S.
Die Summe der Elemente von S
wird somit nach (*) 2k2+k - 1 - (k-1) - 2k = 2k2 - 2k.
Das Produkt der Elemente von F wird ebenfalls gleich 2k2 - 2k.
Dieses Vorgehen funktioniert für alle k≥3, d.h. für alle geraden Zahlen ≥6.
Insgesamt gelingt eine Aufteilung von M = {1, ... , n} in F und S mit Produkt der Elemente von F gleich Summe der Elemente von S für alle n≥5. (Eine triviale Lösung ausserhalb des beschriebenen Rezeptes ist für n = 3 möglich: F = {3}, S = {1, 2}.) Die Rezepte für ungerade und gerade n differieren ein wenig.
Beispiel: n = 10, d.h. k = 5: F = {1, 4, 10}, S = {2, 3, 5, 6, 7, 8, 9}. Summe bzw. Produkt = 40.
Man kann jeder natürlichen Zahl ≥5 den gemäss obigem Verfahren gewonnenen Summen- bzw. Produktwert zuordnen. Dies führt zur Folge 8 12 18 24 32 40 50 ..., deren Aufbau leicht zu durchschauen ist.
In der Online Enzyklopädie der ganzen Zahlfolgen werden weitere Anwendungen dieser Folge gezeigt.
Bsp: n = 6. FLOOR(52/2) = 12. n = 7. FLOOR(62/2) = 18. n = 99: FLOOR(982/2) = 4802.

A, B, C zusammen: 25 Personen
Wir wählen z.B. folgende Variablen für die entsprechenden Personenzahlen:
x: nur B gelöst (gelb)
y: nur C gelöst (grün)
z: B UND C, nicht aber A gelöst (rot)
Hier nochmals die Bedingungen:
(1): A, B, C zusammen: 25
(2): Unter NICHT-A: Doppelt so viele B gelöst wie C gelöst, d.h. x+z=2(y+z)
(3): NUR-A: 1 mehr als "A und mindestens 1 weitere Aufgabe gelöst" (blau markierter Bereich),
d.h. Anzahl Blaue = Anzahl Weisse minus 1
(4): Genau 1 gelöst: Davon die Hälfte NICHT-A (Gelb plus Grün; x + y),
somit NUR-A (Weiss) ebenfalls x + y (im Diagramm eingetragen)
Aus (4) folgt: Anzahl NUR-A gleich x + y.
Aus (3) folgt: Blau markierter Teil: x + y - 1.
Daraus folgt: A: 2x + 2y - 1.
Daraus folgt zusammen mit (1): NICHT-A: 25 - 2x - 2y + 1 oder 26 - 2x - 2y.
Daraus folgt (s. Diagramm): 26 - 2x - 2y = x + y + z oder 26 - 3x - 3y = z (*)
Aus (2) folgt: x + z = 2y + 2z oder x = 2y + z (**)
Setzen wir (**) in (*) ein, folgt: 26-6y-3z-3y=z oder
26 = 9y + 4z.
Die ganzzahlige Lösung ist y = z = 2. Daraus folgt mit (**) x = 6.
Lösung: 6 Personen lösten nur B.
Sei x = dn⋅10n + dn-1⋅10n-1 + ... + d0 eine n+1-stellige natürliche Zahl
mit Ziffernprodukt dn⋅dn-1⋅ ... ⋅ d0 = x2 - 10x - 22.
1) x ist nicht einstellig. Auch ist x ≠ 10 und x ≠ 11. Somit ist x ≥ 12.
2) Es gilt di ≠ 0 für alle i, sonst wäre das Ziffernprodukt x2 - 10x - 22 = 0;
diese Gleichung hat jedoch keine Lösung x in den natürlichen Zahlen.
3) Es gilt
x2 - 10x - 22 = dn⋅dn-1⋅ ... ⋅ d0 < dn⋅10⋅ ... ⋅10 = dn⋅10n
< dn⋅10n + dn-1⋅10n-1 + ... + d0 = x ,
also
x2 - 10x - 22 < x => x2 - 11x - 22 < 0 => x ≤ 12.
Zusammen mit x ≥ 12 folgt x = 12.
In der Tat ist 1⋅2 = 122 - 10⋅12 - 22 = 2.
x = 12 ist somit die einzige Lösung.
Es muss m = 7k + 1 sein.
1.Tag verteilt: 1 + k, restliche Medaillen: 6k
2.Tag verteilt: 2 + (1/7)⋅(6k - 2).
Das bedeutet: 6k - 2 muss durch 7 teilbar sein.
Dies trifft erstmals zu für k = 5.
Wir probieren k = 5 => m = 36:
1. Tag verteilt: 1 + (1/7)⋅35 = 1 + 5 = 6, restliche Medaillen 30
2. Tag verteilt: 2 + (1/7)⋅28 = 2 + 4 = 6, restliche Medaillen 24
3. Tag verteilt: 3 + (1/7)⋅21 = 3 + 3 = 6, restliche Medaillen 18
4. Tag verteilt: 4 + (1/7)⋅14 = 4 + 2 = 6, restliche Medaillen 12
5. Tag verteilt: 5 + (1/7)⋅ 7 = 5 + 1 = 6, restliche Medaillen 6
6. Tag verteilt: 6 + (1/7)⋅ 0 = 6 + 0 = 6, restliche Medaillen 0
Lösung: m = 36, n = 6.
n4 + 4 lässt sich wie folgt faktorisieren:
n4 + 4 = (n2 + 2)2 - 4n2 = (n2 + 2)2 - (2n)2 (erste Binomische Formel). Dies ist nun ein Term der Form "Quadrat minus Quadrat", und solche Terme können mithilfe der dritten Binomischen Formel faktorisiert werden:
(n2 + 2 + 2n)(n2 + 2 - 2n).
Anstelle der 4 sind weitere Zahlen a ∈ ℕ möglich, so dass n4 + a für alle n ∈ ℕ faktorisierbar ist:
n4 + a = n4 + 4b4 = (n2 + 2b2)2 - 4n2b2 = (n2 + 2b2 + 2nb)(n2 + 2b2 - 2nb).
D.h. setze a = 4b4, b∈ ℕ. Unser vereinfachter Fall war b = 1.
p teilt die Differenz (n2 + 1) - (m2 + 1) = n2 - m 2
= (n + m)(n - m). Aber p teilt (n - m) nicht, da p > n - m,
also ist p Teiler von m + n und deshalb auch von (m + n)2 =
m2 + 2mn + n2. Wir subtrahieren n2 + 1 und m2 + 1 (ebenfalls Vielfache von p) und erhalten:
p teilt 2mn - 2 = 2(mn - 1). Folglich (p > 2) ist p Teiler von mn - 1.
Wir vermuten aufgrund von Versuchen: Summe = n. Für n = 1, 2, 3 stimmt die Vermutung.
Sei die Vermutung für 1 bis n bewiesen. Welche Teilmengen kommen für n + 1 dazu?
Es sind {n + 1} und {n + 1} vereinigt mit jeder Teilmenge vom Fall n.
Das ergibt einen Summenzuwachs von 1/(n + 1) + n/(n + 1) = 1.
Folglich ist die Summe im Fall n + 1 gleich n + 1.
Beispiel für eine Zahl, hinter welcher eine Primzahl-Lücke ≥ 9 entsteht:
z = 2⋅3⋅5⋅7⋅9 + 1 = 1891.
Begründung:
z + 1 ist gerade
z + 2 ist durch 3 teilbar
z + 3 ist gerade
z + 4 ist durch 5 teilbar
z + 5 ist gerade
z + 6 ist durch 7 teilbar
z + 7 ist
gerade
z + 8 ist durch 9 teilbar
z + 9 ist gerade
Hinter z sind also mindestens 9 Nachfolgerzahlen nicht prim.
Bemerkung:
Statt das Produkt aller ungeraden Zahlen ≤ 9 zu wählen und 1 zu addieren, genügte es auch, lediglich das Produkt aller Primzahlen ≤ 9 zu wählen und dazu 1 zu addieren. So entstünde z = 211 mit einer nachfolgenden Primzahllücke von mindestens Grösse 9. Tatsächlich folgt auf die Primzahl 211 als Nachfolge-Primzahl 223. Die Lücke hat somit sogar Länge 12.
Für eine Lücke von mindestens Länge 100 bilden wir analog (wir nehmen nur die Primzahlen als Faktoren):
z = 2⋅3⋅5⋅7⋅11⋅ ... ⋅97 + 1 = 2.02...1039. Hinter dieser 40-stelligen Zahl klafft eine Primzahl-Lücke von mindestens Länge 100.
Es gibt somit beliebig grosse Primzahllücken, allerdings "sehr, sehr weit hinten" in der Zahlreihe.
Bemerkung:
Sei g(x) die Länge des längsten primzahlfreien Intervalls bis (und mit) x. Es gilt als grobe Abschätzung:
g(x) ≈ (ln x)2.
Diese Annäherung scheint g(x) eher zu überschätzen. Zudem ist g(x) ja auf gewissen Abschnitten konstant, sodass die Annäherung nur grob stimmt. Zwischen 113 und 127 besteht eine Primzahllücke der Länge 14. Es ist g(127) = ... = g(523) = 14. (Hinter 523 klafft dann eine Lücke der Länge 18.) Die Näherungsformel (ln x)2 liefert jedoch Werte von 24 bis 39, liegt also deutlich zu hoch.
Das führt zu Folgefragen:
Wird die Primzahldichte immer kleiner? - Nicht unbedingt; als Kompensation für die riesigen Lücken könnten dazwischen auch wieder gehäuft Primzahlen vorkommen. Und die grossen Lücken entstehen "astronomisch weit hinten" und sind deshalb gemessen an der Grösse der beteiligten Zahlen doch vergleichsweise "klein".
Die Primzahldichte wird jedoch tatsächlich kleiner; aber es gibt -wie bereits Euklid gezeigt hat- unendlich viele Primzahlen.
Bemerkung 1: Sei π(x) die Anzahl Primzahlen, die kleiner oder gleich x sind.
1850 konnte Tschebyscheff zeigen, dass für hinreichend grosse x gilt:
0.89⋅(x / ln x) < π(x) < 1.1⋅(x / ln x).
Hier das Bild von x / ln x und des von Tschebyscheff angegebenen möglichen Streubereichs (hellblau). Die Steigung der Funktion ist abnehmend (2. Ableitung negativ). Roter Punkt: Effektive Anzahl Primzahlen bis 100'000; π(100'000)=9592. Der rote Punkt liegt noch innerhalb des von Tschebyscheff angegebenen hellblauen Bereichs.
Für x = 1012 ist π(x) ungefähr gleich 1.04⋅ x / ln(x).

Bemerkung 2: Euklids Beweis, dass es unendlich viele Primzahlen gibt in zwei Sätzen zusammengefasst:
Gäbe es nur endlich viele Primzahlen von 2 bis P, so bilde deren Produkt und addiere 1, und du wirst eine Zahl erhalten, die durch keine Primzahl ≤ P teilbar ist. Also muss es Primzahlen > P , d.h., weil P beliebig gross gewählt werden kann, unendlich viele Primzahlen geben.
Quelle: Lebendige Zahlen, Birkhäuser 1981
Die Teiler einer Zahl, z.B. 75, weisen folgende Symmetrie auf (Beispiel n = 75):
1, 3, 5, 75/5, 75/3, 75/1.
Sei n eine solche Zahl.
Seien 1, a, b, ... , n/b, n/a, n ihre Teiler mit Produkt n3.
Daraus folgt, dass n genau 6 Teiler hat:
1, a, b, n/b, n/a, n/1: Das Produkt dieser Teiler ist genau dann gleich n3.
Ergebnis:
Genau die Zahlen mit 6 Teilern erfüllen somit die verlangte Eigenschaft.
Nun fragen wir: Welche Zahlen haben genau 6 Teiler?
Wie bestimmt man die Anzahl Teiler einer Zahl? Beispiel 75 = 31⋅52. Vom Primfaktor 3 kann man die nullte oder die erste Potenz nehmen, vom Primfaktor 5 die nullte, erste oder zweite Potenz. Das ergibt (1+1)⋅(2+1) = 6 Möglichkeiten, Teiler zu bilden.
Allgemein: Sei n = p1a1⋅p2a2⋅ ... in die Primfaktor-Potenzen zerlegt.
Anzahl Teiler: (a1 +1)⋅(a2 +1) = 6
Es ergeben sich die beiden Möglichkeiten 1⋅6 und 2⋅3.
Erste Möglichkeit: a1 +1 = 1 => a1 = 0 und a2 = 5, d.h. n = p10⋅p25 = p25
Zweite Möglichkeit: a1 +1 = 2 => a1 = 1 und a2 = 2, d.h. n = p11⋅p22
Lösung: n ist von der Form p5 oder p⋅q2, (p, q prim).
Beispiele: 243 ist eine Lösung vom Typ p5 und 75 ist eine Lösung vom Typ p⋅q2.
Sei p eine Primzahl grösser als 3.
a)
Es ist p2 + 11 = p2 - 1 + 12 = (p - 1)(p + 1) + 12.
p - 1, p und p + 1 sind drei im Zahlenstrahl der natürlichen Zahlen aufeinanderfolgende Zahlen. p selber ist ungerade und nicht durch 3 teilbar (beachte: p > 3). Deshalb sind entweder p-1 oder p+1 durch 3 teilbar, denn von drei benachbarten Zahlen auf dem Zahlenstrahl ist stets eine durch 3 teilbar - und p ist es nicht.
Deshalb ist (p-1)(p+1) durch 3 teilbar.
p-1 und p+1 sind gerade Zahlen. Als aufeinanderfolgende gerade Zahlen ist eine davon sogar durch 4 teilbar.
Deshalb ist (p-1)(p+1) durch 8 teilbar.
Zusammen ergibt sich: (p-1)(p+1) ist durch 24 teilbar.
Folglich ist p2 + 11 = (p-1)(p+1)+12 als Summe zweier durch 12 teilbare Zahlen ebenfalls durch 12 teilbar, was zu zeigen war.
b)
p2 + 11 ist nach a) ein echtes Vielfaches von 12 (beachte: p > 3). Der Faktor 12 hat bereits 6 Teiler, nämlich {1, 2, 3, 4, 6, 12}. Ein echtes Vielfaches von 12 hat auf jeden Fall noch mehr Teiler, also mehr als 6 Teiler.
Bemerkung:
Die einzige Primzahl, für die p2 + 11 genau 6 Teiler hat, ist 3.
Begründung:
32 + 11 = 20 hat die Teiler {1, 2, 4, 5, 10, 20}. 32 + 11 ist auch nicht durch 12 teilbar, da für p = 3 ein Argument im Beweis links nicht funktioniert. Welches?
Für p = 2 ergibt sich 22 + 11 = 15 mit nur 4 Teilern.
p = 1 ergäbe 12 + 11 = 12, eine Zahl mit 6 Teilern. Aber 1 ist keine Primzahl.
a)
Sei a > 0.
(a -1)2 ≥ 0 ⇒ a2 - 2a + 1 ≥ 0 ⇒ a2 +1 ≥ 2a, daraus folgt (Division durch a > 0):
a + a-1 ≥ 2.
(a > 0 ist wesentlich; bei der Division durch eine positive Zahl bleibt das Ungleichungs-Relationszeichen erhalten.)

Visualisierung: Die Funktion y = x + 1/x für x > 0. Es ist stets y ≥ 2.
b)
n = 1: Der Fall ist trivial: a1 = 1 und (1 + 1) ≥ 21 .
n = 2: Die Zahlen seien a und a-1.
⇒ (1 + a)(1 + a-1) = 1 + a + a-1 + 1 = 2 + (a + a-1) ≥ 2 + 2 = 22 gemäss Teilaufgabe a).
n = 3:
Die Zahlen seien a, b und (ab)-1 mit a, b > 0.
Die Wahl der letzten Zahl berücksichtigt die Voraussetzung, dass das Produkt aller Zahlen gleich 1 sein soll.
(1 + a)(1 + b)(1 + (ab)-1) = 1 + a + b + ab + (ab)-1 + b-1 + a-1 + 1.
Wir haben 23 Summanden.
Die roten Summanden sind die Kehrwerte der schwarzen, fett markierten Summanden.
Es entstehen 4 Paare "Zahl plus Kehrwert", deren Paarsumme gemäss Teilaufgabe a) je ≥ 2 ist:
(1 + 1) + (a +
a-1) + (b + b-1) + (ab + (ab)-1) ≥ 2 + 2 + 2 + 2.
Die Gesamtsumme ist folglich ≥ 23.
Verallgemeinerung:
Auch für beliebige n ∈ ℕ entstehen Summen mit 2n Summanden, die sich zu 2n-1 Paaren des Typs "Zahl plus Kehrwert" mit je Paarsummenwert ≥ 2 gruppieren lassen.
Somit ist die Gesamtsumme ≥ 2⋅2n-1 = 2n.
Gleichheit besteht genau dann, wenn alle
ai = 1 sind.
Hier nochmals die Vereinfachungsregeln:
(1): aaa = 1
(2): bbbb = 1
(3): abab = 1
Wir gewinnen zunächst weitere Vereinfachungsregeln:
Aus (3) entsteht durch Linksmultiplikation mit aa:
aaabab = aa => (wegen (1))
(4):
bab = aa
Aus (3) folgt durch Rechtsmultiplikation mit bbb:
ababbbb = bbb => (wegen (2))
(5): aba = bbb
Nun folgt:
abbaaaabba = abbabba = abaaba (wegen (4)) = (aba)(aba) = (bbb)(bbb) (wegen (5)) = (bbbb)bb = bb (wegen (2)).
Dies ist die maximale Vereinfachung.
Theoretischer Hintergrund:
Dieses Buchstabenspiel erzeugt die Würfeldrehgruppe. a entspricht einer Würfeldrehung um 120° um eine Körperdiagonale des Würfels, b entspricht einer 90°-Drehung um eine Seitenfläche. ab entspricht einer 180°-Drehung um eine Achse, die die Mitten zweier diagonal gegenüberliegender Kanten verbindet.
Exkurs: Die Würfeldrehgruppe
Vereinbarung: Blicken wir in Pfeilrichtung einer Achse, geschehe die Drehung im Gegenuhrzeigersinn. Die Drehachsen seien raumfest gedacht, d.h. drehen mit dem Würfel nicht mit; man kann sie sich als eine Art raumfester "Motoren" vorstellen.
Es gibt 24 Würfeldrehungen (inkl. der neutralen Operation "id").

Drehungen:
keine Drehung: Neutralelement id ("Identität").
orange Achsen: Drehungen um 180° um eine orange Hauptachse (x2, y2, z2).
orange Achsen: Drehungen um 90° oder 270° um eine orange Achse (x1, x3, y1, y3, z1, z3)
grüne Achsen: Drehungen um 120° bzw. 240° um die Körperdiagonalen (a1, a2, b1, b2, c1, c2, d1, d2)
blaue Achsen: Drehungen um 180° um die gezeichneten Kantenmittenachsen (k1, k2, k3, k4, k5, k6).
Zwei Würfeldrehungen, hintereinander ausgeführt, können durch eine einzige Drehung ersetzt werden. Unten stehende Gruppentafel gibt darüber Auskunft. Die Tabelle ist so aufgebaut, dass man die Operationen von rechts nach links liest. a1 x3 bedeute: Führe zuerst x3 aus und dann a1. Gelesen: "a1 nach x3". Diese Kombination lässt sich gemäss Tabelle ersetzen durch z1.

Im Buchstabenspiel von Aufgabe 66 entspricht a der Drehung a1 und b der Drehung z1.
Somit wird die Motivation für die Wahl der Vereinfachungsregeln klar:
aaa sind drei Drehungen a1 mit je 120°, somit eine 360°-Drehung, welche den Würfel wieder in die ursprüngliche Lage bringt; aaa wirkt somit neutral: aaa = 1.
bbbb sind vier 90°-Drehungen um die z-Achse, was ebenfalls keine Veränderung bewirkt: bbbb = 1.
ab bedeutet: a1 z1 = k1 = 180°-Drehung. Somit ist abab neutral: abab = 1.
Unsere Denksportaufgabe 66 ging aus von x2 y2 = z2.
x2 entspricht abbaa (Operationen immer von rechts nach links gelesen!), y2 entspricht aabba. x2 y2 entspricht somit abbaaaabba, was vereinfacht bb ergeben sollte.
Mithilfe der drei Vereinfachungsregeln liess sich dies zeigen.
Die Buchstaben a, b und die drei Vereinfachungsrelationen aaa = bbbb = abab = 1 erzeugen die Würfeldrehgruppe. Diese ist übrigens isomorph zur Symmetrischen Gruppe S4 (jeder Würfeldrehung entspricht eineindeutig eine Permutation der vier Körperdiagonalen).
Um etwas anschaulicher zu werden, färben wir die natürlichen Zahlen ein:
grün: 0, 3, 6, 9, 12, ...: Form 3n
rot: 1, 4, 7, 10, 13, ...: Form 3n + 1
blau: 2, 5, 8, 11, 14, 17, ... : Form 3n - 1
h1) Das Produkt zweier roter Zahlen ist wieder rot: (3n + 1)(3m + 1) = 9mn + 3n + 3m + 1 = 3(3mn+n+m)+1.
h2) Wir betrachten eine zerlegbare blaue Zahl x. Sie enthält gewiss keinen grünen Faktor, sonst wäre die Zahl selber grün (durch 3 teilbar). Enthielte die Zerlegung von x ausschliesslich rote Faktoren, wäre das Produkt, also x, nach h1 selber rot; x ist aber blau. Somit muss x mindestens einen blauen Primfaktor enthalten.
Beispiel: 14 = 2⋅7.
Lösung der Aufgabe:
Gäbe es in der blauen Folge eine grösste Primzahl P, so würden wir alle Primzahlen ≤ P betrachten, wieder wie im ursprünglichen euklidschen Beweis deren Produkt bilden und davon 1 subtrahieren.
Das Ergebnis ist eine blaue Zahl N.
Ist N prim, steht dies im Widerspruch zur Annahme einer grössten blauen Primzahl.
Ist N nicht prim, zerlegt N sich und enthält nach h2 mindestens einen blauen Primfaktor, der jedoch keiner der bisher vorkommenden Primfaktoren sein kann, mithin auch grösser als P ist: erneuter Widerspruch.
Die blaue Folge der Zahlen vom Typ 3n - 1 enthält somit ebenfalls unendlich viele Primzahlen, d.h. die Folge der Primzahlen 2, 5, 11, 17, 23, 29, 41, ... bricht nie ab oder anders gesagt: Es gibt unendlich viele Primzahlen der Form 3n-1.
Weitere Hinweise zur Folge 2, 5, 11, 17, 23, 29, 41, ..: Online Encyclopedia of Integer Sequences OEIS.
Aufgabe und Beweisidee nach Rademacher, Toeplitz: Von Zahlen und Figuren, Springer 1968, p.4f.

Bemerkung:
(2n tief n) ist teilbar durch alle Primzahlen, die zwischen n und 2n liegen. Begründung analog zum Beispiel links.
Beispiele:
(20 tief 10) = 22⋅11⋅13⋅17⋅19
(30 tief 15) = 24⋅32⋅5⋅17⋅19⋅23⋅29
(20 tief 10)+1 = 47⋅3931 (keine Primteiler zwischen 10 und 20)
(30 tief 15)+1 = 13⋅31⋅384'907 (keine Primteiler zwischen 15 und 30)
Rechnen mit Restklassen:
x ≡ a (modulo m) bedeutet: x ergibt bei Division durch m den Rest a.
Beispiel: x ≡ 3 (mod 5). Solche Zahlen sind z.B. ..., -7, -2, 3, 8, 13, 18, ...
Die Restklassenmenge {
..., -7, -2, 3, 8, 13, 18, ...} sei mit [3] bezeichnet.
Die Zahlen ..., -7, -2, 3, 8, 13, 18, ... nennt man kongruent modulo 5,
in Zeichen: ... ≡ -2 ≡ 3 ≡ 8 ≡ 13 ≡... (mod 5).
Die chinesische Eieraufgabe führt auf folgende Kongruenzgleichungen:
x ≡ 1 (mod 2). Gleichbedeutend: x ≡ -1 (mod 2)
x ≡ 2 (mod 3). Gleichbedeutend: x ≡ -1 (mod 3)
x ≡ 4 (mod 5). Gleichbedeutend: x ≡ -1 (mod 5)
x ≡ 0 (mod 7).
Der Chinesische Restsatz (s. unten) löst solche Kongruenzgleichungssysteme. In unserem Fall geht es jedoch auch elementarer:
Gleichungen 1 - 3: Beim Bilden von Zweier-, Dreier- und Fünfergruppen haben wir am Schluss immer 1 Ding zu wenig. Bei welcher Zahl hätten wir beim Bilden dieser Gruppen gerade nichts zu viel und nichts zu wenig? Das ist bei 2⋅3⋅5 = 30 Dingen der Fall. Also ist unsere gesuchte Zahl für die ersten drei Gleichungen 29 oder allgemeiner eine Zahl der Form 30⋅k - 1.
Nun muss die Zahl 30⋅k - 1 noch durch 7 teilbar sein. Wir probieren verschiedene k-Werte: k = 4 liefert erstmals eine Siebnerzahl, nämlich 119. Diese Zahl erfüllt somit alle 4 Gleichungen.
Allgemeine Lösung: x ≡ 119 (mod 2⋅3⋅5⋅7) oder x ≡ 119 (mod 210), d.h.
x
∈ {119, 329, 539, 749, 959, 1169, ...}.
Die Lösung der Eieraufgabe lautet somit: Der Verkäufer hatte 119 Eier im Korb.
Der Chinesische Restsatz
Seien m1, ... , mr paarweise teilerfremde natürliche Zahlen und a1, ... , ar ganze Zahlen, so ist das System
x ≡ a1 (mod m1)
...
x ≡ ar (mod mr)
lösbar und die Lösung ist eindeutig modulo m1⋅ ... ⋅mr.
Beweis-Idee
Man löst das Problem für die ersten beiden Kongruenzgleichungen und führt diese beiden auf eine einzige Gleichung zurück. Dann kann man die dritte Gleichung zufügen und analog vorgehen, usw.
Vorgehen bei zwei Kongruenzgleichungen:
x ≡ a1 (mod m1)
x ≡ a2 (mod m2) .
Da m1 und m2 teilerfremd sind, ist ihr ggT 1 und kann mittels des Algorithmus von Euklid*) als Linearkombination von m1 und m2 dargestellt werden:
1 = u⋅m1 + v⋅m2 .
Daraus folgt:
u⋅m1 ≡ 0 (mod m1)
u⋅m1 ≡ 1 (mod m2)
v⋅m2 ≡ 1 (mod m1)
v⋅m2 ≡ 0 (mod m2)
Daraus wiederum folgt z :=
a2⋅ (u⋅m1) + a1⋅ (v⋅m2) ist kongruent a2 mod m2
und kongruent a1 mod m1, also eine Lösung der beiden ursprünglichen blauen Gleichungen.
Weitere Lösungen erhalten wir durch x ≡ z (mod m1⋅m2).
Wir haben die beiden blauen Gleichungen auf eine einzige, die grüne, zurückgeführt.
Ein Zahlenbeispiel dazu:
x ≡ 3 (mod 5)
x ≡ 4 (mod 7)
1 = 3⋅5 - 2⋅7 (Herleitung siehe unten)
z = 4⋅(3⋅5) - 3⋅(2⋅7) = 18
18 ≡ 3 (mod 5)
18 ≡ 4 (mod 7)
x ≡ 18 (mod 35)
d.h. x ∈ {18, 53, 88, 123, ...}
Die beiden blauen Gleichungen wurden auf eine einzige Gleichung (grün) zurückgeführt.
P.S. für Personen mit Kenntnissen in Ringtheorie:
Da 5 und 7 teilerfremd sind, besteht ein Ring-Isomorphismus
ℤ35 ≅ ℤ5 ⊕ ℤ7 : [18] ↦ ( [3] ; [4] ).
Dass diese Abbildung also umkehrbar ist, ist gleichbedeutend mit der Aussage des Chinesischen Restsatzes.
*) Der Algorithmus von Euklid: ggT(a, b) als Linearkombination von a und b:
ggT(5, 7)
(1): 7 - 5 = 2 (der ggT steckt auch in der Differenz 2)
(2): 5 - 2 = 3 (der ggT steckt erneut auch in der Differenz 3)
(3): 3 - 2 = 1 (der ggT steckt erneut in der Differenz 1, ist also gleich 1)
Es folgt:
1 = 3 - 2 = (5 - 2) - 2 = 5 - (7 - 5) - (7 - 5) =
5 - 7 + 5 - 7 + 5 = 3⋅5 - 2⋅7 = 1 .
Euklid-Rechner hier.
Eine Aufgabe zum Algorithmus von Euklid: Anton schuldet Berta 1 Taler. Anton hat jedoch nur 8-Taler-Stücke und Berta nur 5-Talerstücke. Wie bezahlt Anton seine Schuld? (Aus: Dörte Haftendoorn, Mathematik sehen, Spektrum 2010, p.30).
Lösung: 1 = 2⋅8 - 3⋅5.
Drehen wir das grosse Rad im Gegenuhrzeigersinn, so drehen sich die beiden andern Räder im Uhrzeigersinn.
Das 11er-Rad sollte sich um 3 Zacken im Uhrzeigersinn verschieben.
Das 6er-Rad sollte sich um 5 Zacken im Uhrzeigersinn verschieben.
Das 35-er Rad sollte sich um 8 Zacken im Gegenuhrzeigersinn verschieben.
Wir erhalten folgende Kongruenzgleichungen (siehe Nr. 69):
x ≡ 3 (mod 11)
x ≡ 5 (mod 6)
x ≡ 8 (mod 35)
Die Lösung ergibt: z ≡ 113 (mod 2310).
Chinesischer-Restsatz-Rechner hier.
Das grosse Rad macht dabei 3 Volldrehungen plus 8 Zacken im Gegenuhrzeigersinn.
Das mittlere Rad macht 10 Volldrehungen plus 3 Zacken im Uhrzeigersinn.
Das kleine Rad macht 18 Volldrehungen plus 5 Zacken im Uhrzeigersinn.
Dass eine Lösung existiert, ergibt sich bereits daraus, dass 11, 6 und 35 paarweise teilerfremd sind; jede Konfiguration rechts kann erreicht werden.

Gesucht: 2730 ≡ x (mod 731), minimales x ∈ ℕ.
Wir zerlegen den Exponenten in Zweierpotenzen:
2730 = 2512⋅2128⋅264⋅216⋅28⋅22.
Es ist
22 ≡ 4 (mod 731)
28 ≡ 256 (mod 731)
216 ≡ 477 (mod 731)
232 ≡ 188 (mod 731)
264 ≡ 256 ≡ 28 (mod 731) und folglich
2128 ≡ 477 (mod 731)
2256 ≡ 188 (mod 731)
2512 ≡ 256 (mod 731)
Nun folgt (stets modulo 731):
2730 = 2512⋅2128⋅264⋅216⋅28⋅22
≡ 256⋅477⋅256⋅477⋅256⋅4 = (256⋅256)⋅(477⋅477)⋅256⋅4
≡ 477⋅188⋅256⋅4 = 89'676⋅1024 ≡ 494⋅293 ≡ 144'742 ≡ 4.
Daraus folgt aus dem kleinen Satz von Fermat, dass 731 keine Primzahl sein kann, denn für eine Primzahl müsste sich die Kongruenz 1 ergeben.
In der Tat ist 731 = 17⋅43.
Bemerkung:
Wie führt man etwa 89'676 auf eine kleinere Zahl modulo 731 zurück?
Man dividiert 89'676 durch 731 und erhält 122.6757866...
Nun mulitpliziert man 731 mit 122 und erhält 89'182.
89'676 - 89'182 = 494. Das ist der Rest der Division 89'676 : 731.
Modulo-Rechner von Wolfram für hohe Potenzen
RSA-Verschlüsselung
a) Wir betrachten alle Teiler einer vollkommenen Zahl.
Beispiel: Zahl 6.
Summe der Kehrwerte aller Teiler: 1 + 1/2 + 1/3 + 1/6 = 6/6 + 3/6 + 2/6 + 1/6 = 12/6 = 2.
Bei den gleichnamig gemachten Kehrwerten entsteht im Zähler der Summe bei einer vollkommenen Zahl n stets der Wert 2n; der Nenner ist n.
b) Sei p = 1 + 2 + ... + 2k = 2k+1-1, k ≥ 1, eine Primzahl.
Zeige: n = p⋅2k ist vollkommen, d.h. die Summe aller Teiler ist gleich 2n.
Die Teiler von n = 2k⋅p sind {1, 2, ... , 2k, p, 2p, ... , 2k⋅p }.
Die Teilersumme ist
(1 + 2 + ... + 2k) + p⋅(1 + 2 + ... + 2k) = p + p2 = p⋅(1+p) = p⋅(1+ (2k+1-1)) = p⋅2k+1
c) Sei n eine vollkommene gerade Zahl. Wir spalten n auf in n = 2k⋅u, k maximal, u ungerade.
Zeige: u = 2k+1-1 und u ist prim.
Sei s(u) die Summe aller Teiler von u und s(n) die Summe aller Teiler von n.
Es ist s(n) = (2k+1-1)⋅s(u) und, da n vollkommen ist, = 2n = 2⋅2k⋅u = 2k+1⋅u.
Man mache sich die rot markierte Beziehung am Beispiel der Zahl 28 klar:
Teilersumme: (1+7)+(2⋅1+ 2⋅7)+(22⋅1+22⋅7) = 1⋅(1+7)+2⋅(1+7)+22⋅(1+7)
=(1+2+
22)⋅(1+7) = 22+1⋅(1+7) oder allgemein 2k+1⋅s(u).
Also: (2k+1-1)⋅s(u) = 2k+1⋅u. (*)
Es folgt, dass 2k+1 ein Teiler von s(u) ist (da 2k+1 teilerfremd zu 2k+1-1 ist).
D.h. es gibt ein t ∈ ℕ mit
2k+1⋅t = s(u) (**)
Zusammen mit (*) ergibt sich damit:
(2k+1-1)⋅2k+1⋅t = 2k+1⋅u oder gekürzt mit 2k+1:
(2k+1-1)⋅t = u (***)
u hat folglich die beiden Teiler (2k+1-1)⋅t und t; deren Summe erschöpft jedoch die volle Teilersumme s(u) bereits:
(2k+1-1)⋅t + t = 2k+1⋅t - t + t = 2k+1⋅t = (**) s(u).
(***): u hat somit lediglich 2 Teiler: t = 1 und u selber.
=> u = 2k+1-1, und u ist als Zahl mit nur 2 Teilern eine Primzahl.


Grafik: blau: xP (t) = e-t ; rot / grün: xQ (t) = -t = ln(xP). Eingezeichnet sind die Werte für t = 1.
Wie sähe die Sache aus, wenn P statt bei x = 1 bei x = 1000 startete (mit Anfangsgeschwindigkeit -1000) und Q sich mit konstanter Geschwindigkeit von -1 von x = 0 aus nach links bewegte?
a)
7/13 = 14/26 = 13/26 + 1/26 = 1/2 + 1/26.
Man muss somit 7/13 mit einem geeigneten n erweitern.
Formal: 7/13 = 1/x1 + 1/x2 = (x1+x2) ⁄ (x1⋅x2)
x1+x2 = 7n und x1⋅x2 = 13n.
x2 - 7nx + 13n = 0. Für n = 4 entsteht x2 - 28x + 52 = 0 mit den Lösungen 2 und 26
=> 1/2 + 1/26 = 28/52 = 7/13.
Bemerkung:
Worin liegt der Unterschied zu Teilaufgabe b)? Die Argumentation unter b) trifft auch hier zu. Es zeigt sich, dass auch hier für n≥5 keine Lösungen existieren. Der Unterschied zu b) liegt in den Einzelnachweisen. Bei Teilaufgabe a) zeigen die Einzelnachweise für n=4 eine Lösung; bei b) liefern die Einzelnachweise keine Lösungen.
b)
Wäre 5/13 eine Summe zweier verschiedener Stammbrüche, gälte folgendes:
5/13 = 1/x1 + 1/x2 = (x1+x2)/(x1⋅x2) mit x1, x2 = ganze Zahlen. Das heisst:
x1+x2 = 5n und x1⋅x2 = 13n mit n = ggT(x1+x2 ; x1⋅x2) = natürliche Zahl.
Äquivalent (gemäss Satz von Vieta):
F(x) = x2 - 5nx + 13n hat ganzzahlige Nullstellen x1, x2 .
Dann wäre notwendig die Diskriminante von F(x)=0 eine Quadratzahl, d.h. 25n2 - 52n = Quadratzahl,
bzw. (25n2 - 52n)0.5 wäre eine Ganzzahl. Man zeige, dass dies nicht zutrifft.
Zu zeigen ist: (25n2 - 52n)0.5 ist keine Ganzzahl. (n = natürliche Zahl.)
Die Beweis-Idee, dies zu zeigen entstammt einer Mitteilung von Peter Gallin, Mathematiker und Mathematik-Didaktiker.
Wie man leicht nachrechnet, gilt für alle n ≥ 5:
(5n-6)2 < 25n2-52n < (5n-5)2 => 5n-6 < (25n2 - 52n)0.5 < 5n-5.
Der fett gedruckte Term liegt somit zwischen den benachbarten Ganzzahlen 5n-6 und 5n-5 und kann somit selber keine Ganzzahl sein, was zu zeigen war. Für n = 3 oder n = 4 (Einzelnachweise) liefert (25n2 - 52n)0.5 ebenfalls keine Ganzzahlen. (n = 1 und n = 2 liefern imaginäre Werte und entfallen ohnehin.)
c) Lösungsverfahren von Teilaufgabe b) allgemein:
Sei a / b der gekürzte Bruch. Es muss auf jeden Fall a / b < 1, d.h. a < b sein. Sei a ≠ 2.
Zeige: x2 - anx + bn = 0 hat keine ganzzahligen Lösungen, d.h. (a2n2 - 4bn)0.5 ist keine Ganzzahl.
Sei d: = ⌈ 2b/a ⌉ (= nächst höhere Ganzzahl von 2b / a).
Das erzeugt mit (an - d)2 ab einem bestimmten n die Quadratzahl unterhalb a2n2 - 4bn, die diesem Wert am nächsten kommt.
Wir wünschen wie unter b) : (an - d)2 < a2n2 - 4bn, d.h.
a2n2 - 2and + d2 < a2n2 - 4bn oder d2 < (2ad - 4b)n oder
n > d2 / (2ad - 4b). Für diese Werte von n ist (a2n2 - 4bn)0.5 keine Ganzzahl, sondern liegt zwischen den benachbarten Ganzzahlen a⋅n-d und a⋅n-d+1.
Wir müssen nur noch die Fälle n ≤ d2 / (2ad - 4b) einzeln prüfen.
Bemerkung: Im Fall a = 2 wird d = b und somit (2ad - 4b) = 0 und das Kriterium wertlos, deshalb oben die Forderung a ≠ 2.
Beispiel:
a/b = 7/15.
d = ⌈ 30/7 ⌉ = 5
Für n > 25 / (70 - 60), d.h. für n > 2.5 bzw. n ≥ 3 gibt es keine ganzzahligen Lösungen mehr.
Wir prüfen einzeln noch für n ≤ 2 die Ganzzahligkeit von (a2n2 - 4bn)0.5 = (49n2 - 60n)0.5:
Es gibt auch hier keine ganzzahligen Lösungen.
Somit lässt sich 7/15 nicht als Summe zweier verschiedener Stammbrüche darstellen.
d) a = 2, b = 2k+1 = ungerade Zahl (der Bruch a/b soll ja gekürzt sein).
Man findet durch Analyse von 2/3, 2/5, 2/7, 2/9, ... schnell die allgemeine Formel und
verifiziert sofort:
2/(2k+1) = 1/(k+1) + 1/ [(2k+1)(k+1)]. (k= natürliche Zahl ≥ 1)
Beispiel: k = 6: 2/13 = 1/7 + 1/91.
Aufgabe 1
Behauptung:
Wenn die Koeffizienten a, b und c der Gleichung ax2 + bx + c = 0 alle ungerade Zahlen sind, dann kann die Gleichung keine rationalen Lösungen haben.
Hinweis zur Lösung:
Wie muss die Parität der Diskriminante sein?
Lösung in Peter Gallin:
51 weitere Mathematik-Aufgaben, Orell Füssli 2005, Aufg. 117.
Aufgabe 2
Wenn die Gleichung x2 - bx + c = 0 ganzzahlige Lösungen hat und b und c beide gerade sind, dann ist c sogar durch 4 teilbar. Weshalb?
b ist Summe und c Produkt der beiden ganzzahligen Lösungen z1, z2, denn es ist
x2 - bx + c = (x - z1)(x - z2) = x2 - (z1+z2)x + z1⋅z2 => z1+z2 = b und z1⋅z2 = c.
Wenn aber das Produkt c gerade ist, muss mindestens einer der Faktoren, z.B. z1, gerade sein.
Weil aber auch die Summe b gerade ist, muss auch z2 gerade sein. Dann muss aber das Produkt c (gerade Zahl mal gerade Zahl) durch 4 teilbar sein.
Bemerkung:
Die Aussage kann leicht verallgemeinert werden:
Wenn die Gleichung x2 - bx + c = 0 ganzzahlige Lösungen hat und b und c beide durch die Primzahl p teilbar sind, dann ist c sogar durch p2 teilbar.
Die Begründung verläuft genau gleich wie im rosa Kasten beschrieben. Statt "gerade" setze man "durch p teilbar".
Anders herum formuliert:
Wenn in der Gleichung x2 - bx + c = 0 die Parameter b und c durch die Primzahl p teilbar sind, c jedoch nicht durch p2 teilbar ist, kann die Gleichung keine ganzzahligen Lösungen haben.
Begründung: Annahme: Die Gleichung habe ganzzahlige Lösungen. Dann ist nach der Aussage links der Parameter c durch p2 teilbar: Widerspruch zur Annahme.
Seien die drei für die Lösung in Frage kommenden Teiler von n-1
x = (n-1) ⁄ a, y = (n-1) ⁄ b und z = (n-1) ⁄ c ; a, b, c natürliche Zahlen (und natürlich ebenfalls Teiler von (n-1))
Es gilt (n-1) ⁄ a + (n-1) ⁄ b + (n-1) ⁄ c = n > (n-1) =>
1 ⁄ a + 1 ⁄ b + 1 ⁄ c > 1.
Dies ist jedoch nur möglich wenn unter den 3 Stammbrüchen 1 ⁄ 2 vertreten ist, denn ohne 1 ⁄ 2 wird die Summe 1 nie erreicht. Ebenso muss 1 ⁄ 3 vertreten sein, damit die Summe 1 überschritten wird.
Für den dritten Stammbruch bleiben zum Überschreiten der Summe 1 nur noch die Werte
1 ⁄ 4 oder 1 ⁄ 5.
Fall 1:
(n-1) ⁄ 2 + (n-1) ⁄ 3 + (n-1) ⁄ 4 = 13(n-1) ⁄ 12 = n.
Es folgt 13n-13 = 12n oder n = 13.
In der Tat ist 6 + 4 + 3 = 13 (Summanden = Teiler von 12)
Fall 2:
(n-1) ⁄ 2 + (n-1) ⁄ 3 + (n-1) ⁄ 5 = 31(n-1) ⁄ 30 = n.
Es folgt 31n - 31 =
30n oder n = 31.
In der Tat ist 15 + 10 + 6 = 31 (Summanden = Teiler von 30)
Sei
ax = b2; by = c2; cz = a2 oder
(*): x = b2/a, y = c2/b, z = a2/c.
Aus (*) folgt sofort:
(**):
xyz = b2c2a2 / (abc) = abc.
Aus den Gleichungen (*) folgt:
xy2z4 = a7; yz2x4 = b7; zx2y4 = c7.
Wegen xyz = abc folgt daraus sofort: abc teilt a7, abc teilt b7 und abc teilt c7.
Dann teilt abc selbstverständlich auch die Summe
a7 + b7 + c7.
Zahlenbeispiel:
a = 8, b = 4, c = 16.
8 teilt 16, 4 teilt 256, 16 teilt 64.
8⋅2 = 16; 4⋅64 = 256; 16⋅4 = 64, d.h. x = 2, y = 64, z = 4.
512 teilt 87, 47 und 167 .
Elegante Alternativlösung
Der senkrechte Strich bedeutet: "teilt", d.h. "ist Teiler von" .
a | a; b | c2 | a4; c | a2 => abc | a⋅a4⋅a2 = a7.
Analog (aus Symmetriegründen): abc | b7 und abc | c7.
Wir betrachten die 5 waagrechten und die 5 senkrechten Geraden innerhalb des Gitters.
Nachweis indirekt: Wir nehmen an, es gäbe keine Gerade wie verlangt. Das bedeutet:
Jede der 10 Geraden wird durch einen quer zu ihr liegenden Dominostein unterbrochen.

Wir betrachten z.B. die rot gezeichnete waagrechte Gerade. Sie wird nach Annahme durch einen Dominostein unterbrochen.
Oberhalb und unterhalb jeder Geraden befindet sich stets eine gerade Anzahl 1x1-Quadrätchen, da das grosse Quadrat ja ein 6x6-Quadrat ist. Der quer liegende Dominostein bedeckt von den Flächenteilen ober- und unterhalb der roten Linie je 1 Feld; die noch unbedeckten Teile ober- und unterhalb der roten Linie enthalten somit eine ungerade Anzahl 1x1-Quadrätchen. Daraus folgern wir:
Die in ungerader Anzahl vorhandenen Quadrätchen ober- und unterhalb der roten Linie (s. Abb. links) lassen sich nur lückenlos mit Dominosteinen überdecken, wenn mindestens ein weiterer Dominostein die rote Linie überschreitet, d.h. quer zu ihr liegt.
Dies gilt für jede der 5 waagrechten Geraden. Um sie alle zu unterbrechen sind deshalb mindestens 10 Dominosteine, die quer dazu (also senkrecht) liegen, nötig.
Dasselbe gilt nun auch für die 5 senkrechten Geraden. Man benötigt zu ihrer Unterbrechung nochmals mindestens 10 quer (also waagrecht) liegende Dominosteine.
Total benötigt man also 10 senkrecht und 10 waagrecht liegende Dominosteine, also 20 Steine. Das Brett fasst jedoch nur 18 Steine. Also ist eine Unterbrechung aller Geraden nicht möglich; es muss -wie immer auch die Belegung aussieht- stets mindestens eine Gerade geben, die nicht unterbrochen wird.
Die Eigenschaft E: | ak - ak-1 | = k2 bedeutet:
ak - ak-1 = k2 oder ak-1 - ak = k2, was wiederum heisst:
ak = ak-1 + k2 oder ak = ak-1 - k2.
| Wir finden, wenn wir ak-1 haben, das Folgeglied durch Addition oder Subtraktion von k2. Oder: Wir finden, wenn wir ak haben, das Folgeglied durch Addition oder Subtraktion von (k+1)2. |
Diese Regel erzeugt ausgehend von einer Startzahl eine Vielfalt an Folgen mit der Eigenschaft E.
Nun zeigen wir (Hilfssatz):
Ausgehend von einem beliebigen Folgeglied ak können wir
ak+4 = ak + 4 oder
ak+4 = ak - 4 erreichen (unabhängig von der Stelle k).
Damit können wir dann ausgehend von ak alle Zahlen erreichen, die denselben Viererrest wie ak haben.
Beweis des Hilfssatzes:
Folgende Additions- / Subtraktionskette führt zum Ziel:
ak+4 = ak + (k+1)2 - (k+2)2 - (k+3)2 + (k+4)2 =
ak + k2 + 2k +1 - k2 - 4k - 4 - k2 - 6k - 9 + k2 + 8k + 16 = ak + 4, d.h.
ak+4 = ak + 4 (Summations-Schema + - - +).
Vertauschen wir in der Summation + und -, erhalten wir analog
ak+4 = ak - 4 (Summations-Schema - + + -).
k fällt heraus, was zeigt, dass wir von jedem ak aus in 4 Schritten ak + 4 oder ak - 4 erreichen können, womit der Hilfssatz bewiesen ist.
Hier einige mögliche Folgenanfänge ausgehend von der Startzahl 0:
a) 0, -1, 3, ... (Viererreste 0, 3, 3)
b) 0, 1, -3, 6, ... (Viererreste 0, 1, 1, 2)
Ausgehend von 0 können wir also Zahlen jeder Viererrestklasse erzeugen, und mit dem Vorgehen des Hilfssatzes lassen sich daraus dann sämtliche ganzen Zahlen erzeugen. (Dies gilt dann auch für jede andere Startzahl.)
Seien nun die Startzahl b und die Zielzahl c (ganze Zahlen) gegeben.
Wir bestimmen ihre Viererreste und erzeugen ausgehend von b einen Folgenanfang (siehe oben) bis zu einer Zahl mit gleichem Viererrest wie c. Anschliessend wenden wir den Hilfssatz so lange an, bis wir bei c landen.
Beispiel:
Startzahl b = 0, Zielzahl c = 2021.
Wir starten so: a0 = 0, a1 = 1, a2 = 5
Nun wenden wir immer wieder (504-mal) den Hilfssatz an: a2 = 5, a6 = 9, a10 = 13, ... , a2018 = 2021.
So sieht unsere Folge aus (man verifiziere die Eigenschaft E: | ak - ak-1 | = k2):
| a0 | a1 | a2 | a3 | a4 | a5 | a6 | a2018 | |
| 0 | 1 | 5 | 14 | -2 | -27 | 9 | ... | 2021 |
Diese Folge mit ihren 2019 Elementen ist natürlich viel zu lang; sie dient nur dem Existenzbeweis. Wir finden sofort kürzere Folgen, indem wir die Folge stärker wachsen lassen, bis wir in der Nähe der Zielzahl sind und erst dann zu kleineren Schritten wechseln. Das sähe etwa so aus:
0, 1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, 1015, 1240, 1496, 1785, 2109.
(Diese Folge in OEIS s. hier.)
Wir haben das Ziel um 88 überschritten. Dies können wir wie folgt korrigieren:
Bei a0 rechnen wir statt plus 1 minus 1 (das korrigiert die Folge um minus 2), bei a3 rechnen wir statt plus 16 minus 16 (das korrigiert um weitere minus 32), bei a4 rechnen wir statt plus 25 minus 25 (das korrigiert um minus 50). Wir haben dann vom Überschuss 88 bereits 84 kompensiert ohne die Folge zu verlängern. Zum Schluss wenden wir einmal den Hilfssatz mit ak+4 = ak-4 an (ergibt 4 zusätzliche Folgenglieder). Hier die Folge:
0, -1, 3, 12, -4, -29, 7, 56, 120, 201, 301, 422, 566, 735, 931, 1156, 1412, 1701, 2025,1664, 2064, 2505, 2021.
Diese Folge hat nur noch 23 Elemente (a0 bis a22) und besitzt die Eigenschaft E: | ak - ak-1 | = k2.
Weiterführende Frage: Gibt es noch kürzere E-Folgen mit Start 0 und Ziel 2021?
Klar ist, dass die Anzahl Elemente einer solchen Folge zwischen 19 und 23 liegt.
Ist die Startzahl 0 und die Zielzahl 2025, ist eine E-Folge mit 19 Elementen (a0=0 bis a18=2025) möglich. Wie?
Für eine geraffte Lösung s. auch hier, p 20, Problem 125 und p 105f (solution)
a) Sei n ungerade. Wir betrachten das Beispiel n = 7:
17 + 27 + 37 + 47 + 57 + 67 = 17 + 27 + 37 + (7-3)7 + (7-2)7 + (7-1)7.
Diese Darstellung gelingt bei jeder ungeraden Zahl.
Allgemein:
Jedem Summanden kn der vorderen Summenhälfte entspricht in der zweiten Summenhälfte ein
Summand (n-k)n.
Es ist, da der Exponent n ungerade ist, (n-k)n ≡ (0-kn) ≡ (-k)n ≡ -kn modulo n.
Je ein Summand der vorderen und einer der hinteren Summenhälfte sind also zusammengezählt ≡ 0
modulo n.
Deshalb ist auch die ganze Summe 1n + ... + (n-1)n ≡ 0 modulo n, womit die Behauptung bewiesen ist.
b) Sei n = 2u, u ungerade (n = 2, 6, 10, 14, ...; der Fall n = 2 ist trivial).
Beispiel: n = 6:
16 + 26 + 36 + 46 + 56.
Diese Summe ist ungerade, da sie eine ungerade Anzahl ungerader Summanden enthält (rot gedruckt).
6 kann also diese Summe nicht teilen.
Dies gilt allgemein für alle geraden Zahlen der Form 2u, u ungerade, also für alle geraden Zahlen, die nicht durch 4 teilbar sind.
c) Sei n = 2r⋅u, u ungerade, r ≥ 1, d.h. n sei eine gerade Zahl.
Beispiel: n = 12 = 22⋅3
S:= 112+ 212 + 312+ 412 + 512+ 612 + 712+ 812 + 912+ 1012 + 1112.
Wir betrachten die Zahlen modulo 2r.
Die geraden n-ten Potenzen sind ≡ 0 modulo 2r.
Die ungeraden
n-ten Potenzen sind (Satz von Euler) alle ≡ 1 modulo 2r. *)
(In unserem Beispiel arbeiten wir modulo 4.)
In der Summe S kommen n/2 ungerade Summanden vor, die je ≡ 1 modulo 2r sind.
(Beispiel oben: 6 Summanden je ≡ 1 modulo 4).
Es folgt S ≡ (n/2)⋅1 = 2r-1⋅u ≠ 0 modulo 2r, d.h. 2r teilt S nicht => auch 2r⋅u = n teilt S nicht.
(Beispiel oben: S ≡ 6 ≡ 2 modulo 4, d.h. S ist nicht durch 4 und somit auch nicht durch 12 teilbar.)
Noch ein Beispiel: n = 16
116+ 216 + 316+ ... + 1516 ≡ 1 + 0 + 1 + 0 + ... + 1 modulo 16 ≡ 8 modulo 16, d.h. ergibt bei Division durch 16 den Rest 8, ist folglich nicht durch 16 teilbar.
Zum Satz von Euler (Erklärung rechts) >>>
Beispiel 2r = 16, Gruppentafel modulo 16:
| ⋅ | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
| 1 | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
| 3 | 3 | 9 | 15 | 5 | 11 | 1 | 7 | 13 |
| 5 | 5 | 15 | 9 | 3 | 13 | 7 | 1 | 11 |
| 7 | 7 | 5 | 3 | 1 | 15 | 13 | 11 | 9 |
| 9 | 9 | 11 | 13 | 15 | 1 | 3 | 5 | 7 |
| 11 | 11 | 1 | 7 | 13 | 3 | 9 | 15 | 5 |
| 13 | 13 | 7 | 1 | 11 | 5 | 15 | 9 | 3 |
| 15 | 15 | 13 | 11 | 9 | 7 | 5 | 3 | 1 |
*) Illustration am Beispiel 2r = 8. Die zu 2r teilerfremden Restklassen modulo 8 (1, 3, 5, 7) bilden eine multiplikative Gruppe. Gerechnet wird mit Achterresten. Beispiel: 5⋅5 = 25 ≡ 1 modulo 8, d.h. 25 ergibt bei Division durch 8 Rest 1. Die Gruppenaxiome sind erfüllt, insbesondere hat jedes Element ein Inverses (in diesem Fall ist jedes Element sogar sein eigenes Inverses). Die Gruppenordnung ist 2r-1 = 4. Die Gruppentafel zeigt das Ergebnis einer Multiplikation zweier Gruppenelemente an. Man sieht, dass die Gruppe kommutativ ist (a⋅b=b⋅a):
| ⋅ | 1 | 3 | 5 | 7 |
| 1 | 1 | 3 | 5 | 7 |
| 3 | 3 | 1 | 7 | 5 |
| 5 | 5 | 7 | 1 | 3 |
| 7 | 7 | 5 | 3 | 1 |
Wir zeigen, dass ein Gruppenelement hoch 4 gerechnet 1 ergibt. Dies zeigen wir am Beispiel des Elements 3:
Wir bilden das Element P:= 1⋅3⋅5⋅7.
Nun multiplizieren wir jeden Faktor mit 3: (3⋅1)⋅(3⋅3)⋅(3⋅5)⋅(3⋅7) = 3⋅1⋅7⋅5: Es entsteht wieder P:
P = 1⋅3⋅5⋅7 = (3⋅1)⋅(3⋅3)⋅(3⋅5)⋅(3⋅7) = 34⋅P (letzter Schritt aufgrund der Kommutativität).
Die Gleichung P =
34⋅P multiplizieren wir mit dem Inversen von P und erhalten 1 = 34, was zu zeigen war.
Dies können wir statt mit der 3 mit jedem andern Gruppenelement ebenso durchführen.
Bemerkung: Warum der Beweis, wenn die Gruppentafel sofort zeigt, dass a4 = 1 für jedes Gruppenelement?
Der Beweis gilt eben nicht nur für dieses Beispiel - und wir wollen ja nicht bei jeder Gruppe zuerst die Gruppentafel aufstellen.
Wir erhalten das Resultat: ar-1 = 1 für jedes Gruppenelement a. Dies ist das Resultat, das wir in Aufgabe 80c benötigten.
Beispiel 1: n = 3
Bilde 12345678900. Ist die Zahl nicht durch 3 teilbar, addieren wir bei den Einern eine Zahl. In unserem Fall brauchen wir nichts zu addieren; die Zahl ist bereits durch 3 teilbar. Wir dividieren durch 3 und finden
3⋅4115226300 = 12345678900. (Hier ginge auch bereits 3⋅411522630 = 1234567890.)
Zusatzfrage: Welches ist der kleinst mögliche Multiplikator von 3, der eine Zahl mit sämlichen 10 Ziffern erzeugt?
Antwort: Die kleinste zehnstellige Zahl mit sämtlichen 10 Ziffern ist 1023456789; sie ist bereits durch 3 teilbar.
Es ist somit 3⋅341'152'263 = 1023456789.
Beispiel 2: n = 7
12345678900 ist nicht durch 7 teilbar (ergibt Rest 2). Wir addieren 5. 12345678905 ist durch 7 teilbar:
7⋅1763668415 = 12345678905.
Bei zweistelligen Zahlen n bilden wir 123456789000, bei dreistelligen 1234567890000, usw.
Bei Bedarf addieren wir fortlaufend 1, bis eine durch n teilbare Zahl entsteht.
Der fett gedruckte Vorderteil ändert sich dabei nicht, da bereits bei Additionen im rot markierten Bereich eine durch n teilbare Zahl entsteht.
Beispiel: n = 98. 123456789000 ergibt bei Division durch 98 Rest 6. Wir addieren 92.
123456789092 ist durch 98 teilbar.
98⋅1259763154 = 123456789092.

Wir zeichnen einen Baum (Beispiel oben: n = 4). Die rechte Hälfte ist nicht gezeichnet; die Baumstruktur ist dort symmetrisch zur linken Hälfte (nur sind rechts der Symmetrieachse die Rollen der Null und der Zwei vertauscht). Jeder Pfad entspricht einem zulässigen Wort.
Die Einfärbung oben zeigt folgendes:
Der grün eingefärbte Unterbaum hat dieselbe Struktur wie der ganze Baum, nur steht er zwei Stufen tiefer als dieser.
Die beiden gelb eingefärbten Unterbäume haben ebenfalls von den Ästen her dieselbe Struktur wie der gesamte Baum; sie stehen eine Stufe tiefer.
Sei an die Anzahl Wörter der Länge n bzw. die Anzahl End-Ästchen des n-ten Baumes.
Die Einfärbung oben zeigt sofort die gesuchte Rekursionsformel:
Rekursionsformel: an = 2an-1 + an-2 mit a-1 := 1, a0 := 1; n = 1, 2, 3, ... oder auch: an+1 = 2an + an-1 |
Erläuterung: Sei die Anzahl an der Äste des n-ten Baumes gesucht.
Diese Anzahl an setzt sich zusammen aus den beiden gelb markierten Bäumen, die eine Stufe tiefer sind (Anzahl Äste = 2an-1) und aus dem grün markierten mittleren Baum, der zwei Stufen tiefer steht (Anzahl Äste = an-2).
Das Bild links zeigt den Fall a4 = 2a3 + a2, d.h. 41 = 2⋅17 + 7. Die Rekursionsformel ergibt diese Folge startend mit a1 = 3:
Das Folgeglied wird gewonnen, indem man das letzte Glied verdoppelt und dazu das vorletzte Glied addiert.
Wie bei der Fibonacci-Folge ist auch hier die Quotientenfolge (an / an-1) interessant:
Sie konvergiert gegen 1 + √2, der einen Lösung von x2 - 2x - 1 = 0.
Die Folge
(an-1 / an) konvergiert gegen √2 - 1, das (-1)-fache der andern Lösung von x2 - 2x - 1 = 0.
Analog zum Vorgehen bei der Fibonacci-Folge finden wir eine explizite Formel an = f(n).
Ein heuristischer Zugang zu dieser expliziten Formel (Ideen-Quelle hier):
Ansatz: f(n) = an . Dann gilt nach der Rekursionsformel an = 2an-1 + an-2.
Wir dividieren durch
an-2 und finden: a2 = 2a + 1 oder a2 - 2a - 1 = 0.
Die Lösungen sind u = 1 + √2 und v = 1 - √2.
un und vn erfüllen für alle n ∈ℕ die Rekursionsformel (siehe Spalten un und vn der nachfolgenden Tabelle), aber auch jede Linearkombination von un und vn. (un und vn sind gewissermassen Basislösungen.)
| n | un = (1+√2)n | vn = (1-√2)n | Linearkombination (un + vn) / 2 |
Sollwert an |
| 1 | 1 + √2 | 1 - √2 | 1 | 3 |
| 2 | 3 + 2√2 | 3 - 2√2 | 3 | 7 |
| 3 | 7 + 5√2 | 7 - 5√2 | 7 | 17 |
| 4 | 17 + 12√2 | 17 - 12√2 | 17 | 41 |
Wir sehen: Die entstehenden Werte sind um eine Zeile verschoben. Wir erhalten den Sollwert, wenn wir anstelle des Exponenten n den Exponenten n+1 wählen:

Interessant ist, dass wir für die Berechnung dieser ganzzahligen Folge die irrationale √2 benötigen. Diese ist an der Konstruktion der Elemente der Zahlfolge beteiligt und verschwindet nach getaner Arbeit wieder. Um unsere Zahlenfolge, die sich ganz im Bereich der natürlichen Zahlen abspielt zu "knacken", müssen wir uns hier ins Feld der irrationalen Zahlen begeben! Ähnliches geschieht bei gewissen reellen Funktionen, die erst im Bereich der komplexen Ebene vertieft verstanden werden können.
Bemerkung:
Die Folgenglieder 1, 3, 7, 17, 41, 99, ... sind auch die Zähler in der Kettenbruchentwicklung von √2 (siehe rechts).
Die ersten 6 Brüche dieser Entwicklung lauten:
1/1, 3/2, 7/5, 17/12, 41/29, 99/70.
Interessant ist, dass sowohl die Zähler- als auch die Nennerfolge die Rekursionsformel
an+1 = 2an + an-1 (mit je verschiedenen Anfangsbedingungen) erfüllen.
Die Folge 3, 7, 17, 41, 99, ... repräsentiert auch die Anzahl n-Schritt-Wanderungen (n = 1, 2, 3, ...) in West-, Nord- und Ostrichtung, wenn nach einem West-Schritt nicht gleich ein Ost-Schritt und umgekehrt folgen darf (was ja als Wanderung sinnlos wäre).
Die Kettenbruchentwicklung von √2:
Der grün markierte Teil ist bei unendlicher Fortsetzung gleich dem ganzen Ausdruck x, also auch gleich x:

Der Elferrest 0 kommt auch in der Produktfolge (ai⋅bi) nicht vor, da 11 eine Primzahl ist:
Ist nämlich 11 Teiler eines Produkts x⋅y, so muss 11, da Primzahl, Teiler von x oder von y sein. Haben also weder x noch y Elferrest 0, so auch das Produkt x⋅y nicht.
Nun überlegen wir wie folgt:
Es ist 1⋅2⋅...⋅10 = a1⋅...⋅a10 = b1⋅...⋅b10 = 10! und diese Zahl hat Elferrest 10. (*)
Annahme: Die Folge (ai⋅bi), reduziert auf ihre Elferreste, habe lauter verschiedene Elferreste, also die Elferreste 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. (Der Rest 0 erscheint nicht; s. oben.)
Dann muss aber a1b1⋅ ... ⋅a10b10 wegen (*) Elferrest 10 haben.
Aber a1b1⋅ ... ⋅a10b10 = (a1⋅...⋅a10)⋅(b1⋅...⋅b10) hat Elferrest 10⋅10 = 100, d.h. Elferrest 1: Widerspruch.
Folglich hat die auf die Elferreste reduzierte Folge (ai⋅bi) nicht lauter verschiedene Elferreste, d.h. mindestens zwei Elferreste sind gleich.
Illustration zum Beweis:
| Folge (an) | 3 | 2 | 1 | 4 | 6 | 9 | 5 | 10 | 8 | 7 |
| Folge (bn) | 5 | 4 | 7 | 1 | 6 | 3 | 8 | 10 | 9 | 2 |
| Folge (ai⋅bi) | 15 | 8 | 7 | 4 | 36 | 27 | 40 | 100 | 72 | 14 |
| Elferreste der Folge (ai⋅bi) | 4 | 8 | 7 | 4 | 3 | 5 | 7 | 1 | 6 | 3 |
Wie der Beweis links fordert, hat das Produkt der Zahlen der untersten Zeile obiger Tabelle Elferrest 1. Kämen alle Elferreste 1 bis 10 vor, müsste jedoch das Produkt Elferrest 10 haben.
Wir führen den Beweis anhand des Beispiels p = 7.
Nachstehend die Gruppentafel der multiplikativen Restklassengruppe modulo 7 (Restklassen 1 bis 6):
| ⋅ (mod 7) | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 2 | 4 | 6 | 1 | 3 | 5 |
| 3 | 3 | 6 | 2 | 5 | 1 | 4 |
| 4 | 4 | 1 | 5 | 2 | 6 | 3 |
| 5 | 5 | 3 | 1 | 6 | 4 | 2 |
| 6 | 6 | 5 | 4 | 3 | 2 | 1 |
(1): Wir sehen, dass nur 1 und 6 ihr eigenes Inverses sind: 1⋅1≡1 und 6⋅6≡1 (mod 7).
Alle übrigen Elemente haben nicht sich selber als Inverses:
2 und 4 sind invers zueinander; 3 und 5 sind invers zueinander.
Wir beweisen (1) am Schluss.
(2): Es gilt offensichtlich:
(p - k)(p - k-1) ≡ 1 (mod p) für alle Inversen-Paare (k, k-1), 2 ≤ k, k-1≤ (p - 2).
Im Beispiel p = 7 sieht das so aus:
(p-2)(p-4) ≡ 1 (mod p)
(p-3)(p-5) ≡ 1 (mod p)
(3): Wir betrachten nun (p - 2)! = (p - 2)⋅(p - 3)⋅ ... ⋅2.
Wir nehmen den Faktor (p - 2) und seinen "Partner" (p - 2-1).
Das sind nach (1) zwei veschiedene Faktoren. Dann nehmen wir einen weiteren Faktor von
(p - 2)! und seinen Partner, usw. Am Schluss haben wir lauter Faktoren-Paare wie z.B.
(p - 2)(p - 2-1), die alle ≡ 1 modulo p sind. Also ist auch das ganze Produkt (p - 2)! ≡ 1 modulo p.
Beispiel p = 7:
(p-2)! = 5! = [(p-2)(p-4)]⋅[(p-3)(p-5)] = (5⋅3)⋅(4⋅2) ≡ 1⋅1 ≡ 1 (mod 7).
Beispiel p = 17: Inversenpaare (2;9), (3;6), (4;13), (5;7), (8;15), (10;12), (11;14).
Damit
können wir (17 - 2)! modulo 17 herstellen und zeigen, dass dies ≡ 1 (mod 17) ist:
(17-2)! = 15! =
(17-2)(17-9)⋅(17-3)(17-6)⋅...⋅(17-11)(17-14) =
(15⋅8)⋅(14⋅11)⋅(13⋅4)⋅(12⋅10)⋅(9⋅2)⋅(7⋅5)⋅(6⋅3) ≡ 1⋅1⋅1⋅1⋅1⋅1⋅1 = 1 (mod 17)
Zu zeigen ist noch (1):
Wir zeigen, dass die Elemente modulo p, die ihr eigenes Inverses sind, nur (p-1) und 1 sein können:
Sei x
sein eigenes Inverses, d.h. x⋅x ≡ 1 (mod p).
Das bedeutet: x2 - 1 ≡ 0 (mod p), d.h. p teilt x2 - 1 = (x + 1)(x - 1).
Weil p prim ist, teilt p entweder (x+1) oder (x-1).
Das bedeutet entweder x+1 ≡ 0 oder x-1 ≡ 0, d.h. x ≡ -1 ≡ (p - 1) oder x ≡ 1 (modulo p)
Sei q(x) die Quersumme von x. Man bestimme q(q(q(20002000))).
20002000 = 22000⋅10002000 = 22000⋅106000.
Der zweite Faktor trägt nichts zur Quersumme bei; er liefert nur Nullen.
Wir suchen somit q(q(q(22000))).
Sei log(x) der Zehnerlogarithmus von x.
Es ist log(22000) = 2000⋅log(2) = 602.059991...
Somit ist 22000 eine 603-stellige Zahl. q(22000) kann dann höchstens gleich 9⋅603 = 5427 sein.
q(q(22000)) kann dann höchstens gleich 31 sein (Quersumme von 4999) und q(q(q(20002000))) ist dann höchstens gleich 11 (Quersumme von 29).
Es ist 22000 = 22⋅1000 = 41000.
Es ist 43 ≡ 1 (mod 9) => 41000 = 4⋅4999 = 4⋅(43)333 ≡ 4⋅1 ≡ 4 (mod 9).
Resultat: q(q(q(22000))) = q(q(q(20002000))) = 4.
A = {7, 8, 9, 10}, B = {2, 3, 4, 5, 6}. Dann ist a / b = 5040 / 720 = 7.
(1): n = p1k1⋅p2k2⋅ ...
(2): dn = (k1+1)⋅(k2+1)⋅...
(3): dn3 = 4n
Bemerkung:
Die Lösung rechts ist kein formal lückenloser Beweis. Die Aussagen, dass es keine weiteren Lösungen gibt, müssten mit Ungleichungen begründet werden.
a) Wegen (3) ist 4n = 2⋅2⋅n eine Kubikzahl; mindestens ein weiterer Faktor 2 muss deshalb in n vorkommen. Die Anzahl k1 der in n vorkommenden Faktoren 2 beträgt 3n1+1; n1 ∈ {0,1,2,...}.
n enthält also auf jeden Fall mindestens einen Primfaktor 2.
Die übrigen Primfaktoren pi kommen 3⋅ni -mal vor; ni ∈ {0,1,2,...}.
b) Nach (2) ist dn = (3n1+ 2)⋅(3n2 + 1)⋅ ... . Diese Zahl ist ≡ 2 modulo 3, d.h. nicht durch 3 teilbar. Folglich sind auch dn3 und n = 4⋅dn3 nicht durch 3 teilbar. n enthält somit den Primfaktor 3 nicht. Der nach 2 nächste Primfaktor, der möglich ist, ist somit 5.
c) Betrachten wir zunächst nur die reinen Zweierpotenzen: 2 ist eine Lösung des Problems (n1 = 0).
Die nächste Möglichkeit
(n1 = 1) ist 24 = 16, erfüllt jedoch die Bedingung (3) nicht.
Mit n1 = 2 folgt 128. Diese Zahl erfüllt die Bedingung und ist eine weitere Lösung.
n1 = 3 ergibt die Zahl 1024 mit 11 Teilern. 113 = 1331 < 4⋅1024. Für noch höhere n1-Werte läuft 4n dem Wert dn3 immer weiter davon; es gibt keine weiteren Zweierpotenzlösungen mehr.
Nehmen wir nun zum Primfaktor 2 noch den Primfaktor 5 hinzu.
2⋅53 = 250 ist keine Lösung. (8 Teiler; 512 < 4⋅250).
2⋅56 = 31'250 hat 14 Teiler: 2744 < 4⋅31'250 ist keine Lösung. Für höhere Potenzen von 5 entfernt sich 4n weiter von dn3 .
24 ⋅53 = 2000 hat 20 Teiler. 203 = 4⋅2000, d.h. 2000 ist eine weitere Lösung.
Höhere Potenzen von 2 und 5 ergeben keine Lösungen mehr, 4n läuft davon.
Primfaktoren 7 und höher: Sie ergeben keine Lösungen mehr; 4n läuft dem Wert dn3 davon.
Fazit: Die Lösungen sind 2, 128 und 2000.
Hier nochmals die Formel für die Anzahl Teiler einer Zahl n = p1k1⋅p2k2⋅ ... :
dn = (k1+1)⋅(k2+1)⋅... |
Dann ist n = p1k1⋅p2k2⋅ ... eine Quadratzahl.
Die Umkehrung gilt ebenfalls.
Bild a)
Quadratseiten halbiert: Aus 1 Quadrat entstehen 4, Zuwachs +3.
Bild b)
Die Teilquadrate können erneut mit einem "Fensterkreuz" (rot) versehen werden: Zuwachs pro Fensterkreuz +3.
Bild c)
Zwei Quadratseiten gedrittelt. Aus einem Quadrat entstehen 6 (5 kleine und 1 grosses).
Bild d)
Die Teilquadrate können erneut beliebig unterteilt werden.

 Mrs. Perkins' Quilt
Mrs. Perkins' Quilt
Bemerkung:
Die Unterteilungen a), b) und c) sind speziell: Sie beinhalten Teilquadrate mit maximal zwei verschiedenen Grössen. Bei d) sind 3 Sorten von Unterquadraten im Spiel. Will man weniger, bietet sich das 3x3-Schachbrett an.
Nochmals zu c)
Werden zwei Quadratseiten durch k geteilt (statt wie in c durch 3), so entstehen, wenn wie in c) vorgegangen wird, aus dem einen Quadrat 2k Quadrate.
Somit ergibt sich: Ist n gerade, ist eine Unterteilung stets möglich für n ≥ 4 (Vorgehen wie bei c).
Alle n = 2k, k ≥ 2, sind somit möglich. Aber durch Einsetzen eines Fensterkreuzes (rot) in ein Teilquadrat ist auch 2k + 3 als Unterteilungszahl möglich, also 7, 9, 11, 13, 15, ... , d.h. alle ungeraden n ≥ 7.
Abb. d) zeigt z.B. den Fall n = 9 hervorgehend aus c) n = 6.
Unterteilungen sind also möglich für n = 4, sowie für alle n ≥ 6.
n = 1 ist trivial und ist keine echte Unterteilung.
Dass n mindestens 4 sein muss, zeigt folgende Überlegung:
Jede Ecke des ursprünglichen Quadrats muss durch ein Teilquadrat (Seitenlänge kleiner als diejenige des Ausgangsquadrats) überdeckt werden. Somit sind mindestens 4 Teilquadrate nötig.
Eine Überdeckung mit 5 Teilquadraten ist nicht möglich. Wie könnte dies begründet werden?
Bemerkung:
Setzt man Zusatzbedingungen, etwa dass bei der Unterteilung keine Rechtecke entstehen dürfen ("einfache Unterteilung"), oder dass die Teilquadrate alle verschiedene Grösse haben müssen ("perfekte Unterteilung"), wird die Sache komplizierter. Mrs. Perkins' Quilt links ist weder einfach (gelbes Rechteck oben) noch perfekt.
Link.
Siehe auch Aufgabe 41 und
http://www.squaring.net/history_theory/brooks_smith_stone_tutte.html
https://mathworld.wolfram.com/MrsPerkinssQuilt.html
Wir zeigen indirekt, dass das Produkt P von 5 aufeinander folgenden natürlichen Zahlen (≠0) nie eine Quadratzahl sein kann:
Annahme: Es gebe eine solche Fünferfolge, deren Produkt eine Quadratzahl sei.
(1): Sei p ein Primfaktor einer der 5 Zahlen mit p ≥ 5. Dann kommt p lediglich in einer dieser Zahlen vor (und nicht in den andern vier). Soll das Produkt P eine Quadratzahl sein, muss folglich p noch ein zweites Mal (allgemein: insgesamt eine gerade Anzahl mal) in der Zahl vorkommen. Ist zudem diese Zahl nicht durch 2 und nicht durch 3 teilbar, ist sie somit eine Quadratzahl.
(2): Wir betrachten das Bild rechts, welches P = (x-2)⋅(x-1)⋅x⋅(x+1)⋅(x+2) zeigt.
Grüner Rahmen: Die Zahl sei durch 3 teilbar.
Rotes Feld: Die Zahl sei durch 2 teilbar.
Es entstehen die 6 Fälle, die im Bild rechts dargestellt sind.
Bei a), b), c) und f) bleiben je zwei Zahlen ungefärbt, sind also weder durch 2 noch durch 3 teilbar.
Nach (1) sind sie somit Quadratzahlen. Mit Ausnahme der Quadratzahlen 1 und 4 liegen jedoch keine zwei Quadratzahlen auf dem Zahlenstrahl so eng (d.h. innerhalb eines "Fünferfensters") zusammen: Wir erhalten einen Widerspruch zur Annahme.
(3): Es verbleiben die Fälle d) und e). Wir können uns auf d) beschränken; e) ist symmetrisch dazu.
Betrachten wir also Teilbild d). Ist x eine durch 4 teilbare Zahl, so sind (x-2) und (x+2) lediglich durch 2 teilbar (das liegt in der "Natur" der Zweierreihe), enthalten also je genau einen Primfaktor 2. Wenn P eine Quadratzahl sein soll, muss somit x den Primfaktor 2 in gerader Anzahl enthalten. x ist nicht durch 3 teilbar. Alle Primfaktoren ≥5 sind nach (1) ebenfalls in gerader Anzahl vorhanden, also ist x eine Quadratzahl, ebenso die ungefärbte Nachbarzahl (x - 1). Das kann nicht sein: Widerspruch zur Annahme.
(4): Es verbleibt (immer noch Zeile d) der Fall, dass x den Primfaktor 2 genau einmal enthält. x (nicht durch 3 teilbar!) ist dann das Doppelte einer Quadratzahl. (x + 2) ist dann durch 4 teilbar, enthält also den Faktor 2 mindestens doppelt. Zudem ist (x + 2) nicht durch 3 teilbar. (x + 2) ist also entweder das Doppelte einer Quadratzahl oder selber eine Quadratzahl. x und (x + 2) können jedoch nicht gleichzeitig das Doppelte einer Quadratzahl sein (sie liegen zu nahe beisammen); ebenso wenig können (x - 1) und (x + 2) gleichzeitig Quadratzahlen sein (sie liegen ebenfalls zu nahe beisammen*): erneuter Widerspruch zur Annahme.
*Anmerkung: Nur 1 und 4 liegen im Abstand 3 zueinander. Lässt man dies zu, so wäre x-1 = 1, d.h. x=2 und es entsteht das Produkt 0⋅1⋅2⋅3⋅4 = 0 = Quadratzahl. Dies ist die einzige triviale "Lösung", wenn 0 zugelassen wird.

Bild oben: grün: durch 3 teilbar; rot: durch 2 teilbar, unmarkiert: weder durch 2 noch durch 3 teilbar.
Wäre das Produkt P der fünf Zahlen eine Quadratzahl, so müssten die unmarkierten Zahlen (Primfaktoren alle ≥5) ebenfalls Quadratzahlen sein.
Da Quadratzahlen auf dem Zahlenstrahl jedoch (mit Ausnahme von 4 und 1) nie so eng beieinander liegen, verbleiben zur genaueren Untersuchung nur noch die Fälle d) und e).
Lösung der Alternativaufgabe:
P:= (x - 1)⋅x⋅(x + 1).
Generell: Sei p ein Primfaktor ≥3 in einer der Zahlen. Dann kommt er lediglich in dieser Zahl vor. Soll
P eine Quadratzahl sein, muss p in gerader Anzahl vorkommen. Ist die Zahl nicht durch 2 teilbar, ist sie dann folglich eine Quadratzahl.
Fall 1: x gerade => (x - 1) und (x + 1) ungerade und folglich Quadratzahlen: Widerspruch, da Quadratzahlen auf dem Zahlenstrahl nicht so eng beieinander liegen können.
Fall 2: x ungerade => x = Quadratzahl. Damit P Quadratzahl ist, muss folglich (x-1)(x+1) = x2-1 eine Quadratzahl sein: Das ist unmöglich, denn dann wären die Nachbarzahlen x2 und x2-1 je Quadratzahlen, was nicht sein kann. (Dies träfe wieder nur für die triviale Lösung x=1, d.h. 0⋅1⋅2 = 0 zu.)
Wie viele Stangen kann man maximal entfernen?
Entfernt man in einer Zeile eine Stange, so darf die Nachbarzeile keine Leerstelle enthalten, da sonst Sichtkontakt bestünde. Dasselbe gilt für jede Spalte. Es kann also höchstens jede zweite Zeile und jede zweite Spalte Leerstellen beinhalten.
Die rechts gezeichnete Variante zeigt somit maximal viele Leerstellen,
insgesamt [(u+1)/2]2 Leerstellen.

Hier nochmals die Axiome:
A1: 1 ist eine erlaubte Figur.
A2: Ist A eine erlaubte Figur, so auch A0.
A3: Ist A eine erlaubte Figur, so auch 1A1.
1. 11001 ist wie folgt herstellbar:
A1: 1; A2 zweimal angewendet: 100. A3 angewendet: 11001.
Regel R zur Erzeugung:
"A1, A2, A2, A3".
2. 011 ist nicht herstellbar, denn jede erlaubte Figur hat links eine 1.
3. Wir zeigen die Möglichkeit, aus A die Figur 11A herzustellen am Beispiel A=11001, erzeugt mit Regel R:
111 kann erzeugt werden ("A1,A3"). Wende nun darauf Regel "R ohne A1" an ("A2,A2,A3"):
111, 1110, 11100, 1111001 = 11(11001) = 11A. Dies kann mit jedem A durchgeführt werden.
Allgemein:
Sei A durch die Regel R erzeugt (Start mit A1).
Sei R' die Regel, die A erzeugt, jedoch ohne A1 am Anfang.
Wir starten statt mit 1 mit 111 (erzeugt durch "A1,A3") und lassen R' folgen.
Es
entsteht 11A.
Äquivalent: Wir nehmen die Regel R, die A erzeugt und schieben als zweiten Schritt A3 ein.
Es entsteht 11A.
1. Minimum = 45 = 1+ ... +9. Maximum = 315, z.B. 61+72+83+94+5; die Zehnerziffern sind dabei gesetzt, die fünf Einerziffern können noch beliebig permutiert werden.
Man beachte, dass Nullen nicht vorkommen dürfen!
Es gibt somit 5! = 120 Möglichkeiten, Summe 315 zu erreichen.
Da keine Null vorkommen darf, sind maximal 4 zweistellige Zahlen möglich.
2. Die Summe aller neun Ziffern ist 45. Sei x die Summe der Zehnerziffern. Dann ist die Summe der Einerziffern gleich 45-x. Die Summe s beträgt dann 10x + 45-x = 9x+45. s ist somit immer durch 9 teilbar.
3. Kann jede Neunerzahl zwischen 45 und 315 erreicht werden? - Ja.
Vorgehen: In 9x+45 den Wert x bestimmen = Summe der Zehnerziffern.
x liegt zwischen 0 und 30.
Es gibt stets eine passende Zehnerziffernkombination mit maximal 4 Zehnerziffern mit einer solchen Summe.
Beispiel: 297 = 9x+45 => x = 28. Mögliche Zehner: 9, 8, 7, 4.
91 + 82 + 73 + 45 + 6 = 297.
Andere Möglichkeit, z.B.
Zehner: 9, 8, 6, 5. 91 + 82 + 67 + 54 + 3
= 297.
4. Die Addition, die 99 ergibt, enthält eine zweistellige Zahl oder zwei oder drei zweistellige Zahlen.
Es ist 9x+45 = 99, somit x = 6, d.h. die Summe der Zehnerziffern ist gleich 6.
Fälle:
Keine Zehnerziffer, d.h. alle Summanden einstellig: 99 wird nicht erreicht.
Eine Zehnerziffer, d.h. ein Summand zweistellig: Zehnerziffer = 6. Für die zugehörige Einerziffer bleiben 8 Möglichkeiten.
Beispiel: 65 + 1 + 2 + 3 + 4 + 7 + 8 + 9 =
99.
Zwei Zehnerziffern, d.h. zwei Summanden zweistellig: 5 und 1 bzw. 4 und 2 als Zehnerziffern. An die 5 können 7 mögliche Einerziffern angehängt werden, an die 1 dann noch 6, das ergibt 42 Möglichkeiten. Dasselbe gilt für die 4 und die 2 als Zehnerziffern: nochmals 42 Möglichkeiten.
Beispiel: 43 + 29 + 1 + 5 + 6 + 7 + 8 = 99.
Drei Zehnerziffern, d.h. drei Summanden zweistellig: 3, 2 und 1 als Zehnerziffern. An die 3 können sechs, an die 2 fünf und an die 1 noch vier Einerziffern angehängt werden: 120 Möglichkeiten.
Total: 8 + 42 + 42 + 120 = 212 Möglichkeiten.
5. Auch wenn mehr als zweistellige Zahlen zugelassen sind, ist die Summe s durch 9 teilbar. Beispiel für den Fall ein-, zwei- und dreistelliger Zahlen: Sei x die Summe der Hunderterziffern, y die Summe der Zehnerziffern. Dann ist 45-x-y die Summe der Einerziffern. s ist dann gleich 100x+10y+45-x-y = 99x+9y+45, also durch 9 teilbar.
Für vier- und höherstellige Zahlen geht die Überlegung analog.
6. Hunderterziffern: 9, 8 und 7. Zehnerziffern: 6, 5 und 4. Einerziffern: 3, 2 und 1.
Summe: 2556.
Fibonacci-Folge: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
Wir können wie folgt aufteilen:
| Grp 1 | 1 | 1 | 8 | 13 | 21 | 144 | ||||
| Grp 2 | 2 | 3 | 5 | 34 | 55 | 89 |
oder
| Grp 1 | 1 | 2 | 3 | 21 | ||||||
| Grp 2 | 1 | 5 | 8 | 13 |
Die gleich eingefärbten Felder (je 6 Felder) sind summengleich und erfüllen die beiden Aufteilungs-Bedingungen.
Im ersten Fall ist für n = 6, 12, 18, 24, ... , also für n = 6k, k = 1, 2, 3, ..., eine Aufteilung möglich.
Im zweiten Fall ist für n = 2, 8, 14, 20, ..., also für n = 2+ 6k, k = 0, 1, 2, 3, ..., eine Aufteilung möglich.
n = 2022 ist von der Form 6k, somit ist eine Aufteilung möglich.

Beispiele zur gaussschen Aufrundungsklammer ⌈ ⌉:
⌈2⌉ = 2
⌈2.1⌉ = 3
Es wird auf die nächste Ganzzahl aufgerundet, sofern die Zahl nicht bereits eine Ganzzahl ist. Diese Operation heisst auch "ceiling":
ceil(2) = 2
ceil(2.1) = 3
Zum Schritt y = 15 - ⌈ x/3 ⌉ (Situation nach einem Schritt):
Vorher: {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21} ausgelegt auf 3 Stapel (von unten nach oben):
| Die 3 Stapel nach 1 Schritt | ⌈x / 3⌉ | 8 - ⌈x / 3⌉ |
7 + 8 - ⌈x / 3⌉ |
| 19 20 21 | 7 | 1 | 8 |
| 16 17 18 | 6 | 2 | 9 |
| 13 14 15 | 5 | 3 | 10 |
| 10 11 12 | 4 | 4 | 11 |
| 7 8 9 | 3 | 5 | 12 |
| 4 5 6 | 2 | 6 | 13 |
| 1 2 3 | 1 | 7 | 14 |
Nachher am Beispiel x = 15: {∗,∗,∗,∗,∗,∗,∗,21,18,15,12,9,6,3,∗,∗,∗,∗,∗,∗,∗}: Rang 10.
Varianten
27 Karten; Stapel zuerst umgedreht. Stapel mit gemerkter Karte ins Sandwich:
Da die drei Stapel umgedreht werden, lauten die Formeln (x, y, z, s wie oben):
y = 9 +⌈ x/3 ⌉, z = 9 +⌈ y/3 ⌉ und s = 9 +⌈ z/3 ⌉.
Wird der Stapel mit der gemerkten Karte stets ins Sandwich genommen, landet die gemerkte Karte nach drei Vorgängen stets auf Rang 14, d.h. auf dem mittleren Rang der 27 Karten.
27 Karten; Stapel zuerst umgedreht. Stapel mit gemerkter Karte entweder nach unten, ins Sandwich oder nach oben:
Statt nun den Stapel mit der gemerkten Karte stets in die Mitte des Gesamtpakets zu bringen, kann man in jeder der drei Phasen diesen Stapel entweder nach unten, in die Mitte oder nach oben bringen. Das ergibt insgesamt 27 Kombinationen, die am Schluss je einen andern Rang der gemerkten Karte im umgedrehten Gesamtpaket ergeben.
| Man kann den Trick, wie er rechts beschrieben ist auch mit verdeckten Teilstapeln durchführen. Die vorführende Person sieht dann nie die Kartenbilder, was noch mysteriöser wirkt. Allerdings muss man dann das Gesamtpaket von unten nach oben auf die drei Teilstapel abspulen. Alle Teilstapel und das Gesamtpaket haben dann stets die Rückseite oben. Die Person, die sich die Karte gemerkt hat, muss dann die verdeckten Teilstapel durchsehen und anzeigen, in welchem Teilstapel ihre Karte liegt, oder die vorführende Person fächert die Stapel -Rückseite gegen sich- auf und erfragt den betreffenden Teilstapel. Der Rest geht gleich wie rechts beschrieben. Der Trick ist so etwas verblüffender, aber auch etwas umständlicher und langsamer als mit offenen Teilstapeln. |
Wie kann man die gemerkte Karte z.B. auf Rang 6 im umgedrehten Schlusspaket bringen?
Wir betrachten die Zahlen von 0 bis 26 im Dreiersystem. Für Schlussrang 6 verwandeln wir die die 6. Zahl dieser Reihe, also die Zahl 6-1 = 5, ins Dreiersystem: 012 (links Neuner, Mitte Dreier, rechts Einer). Das ergibt, beginnend mit der Einerziffer, die Vorgehensweise: 2 bedeutet: in Phase eins Stapel mit der gemerkten Karte nach unten. Dann folgt die 1: in Phase zwei Stapel in die Mitte. Dann folgt die 0: in Phase drei Stapel nach oben.
Die gesuchte Karte wird schiesslich auf Rang 6 landen.

Allgemein: Wir möchten Rang x erreichen. Seien a|b|c die Ziffern der Zahl x-1 im Dreiersystem.
Dann ist y = 9c+⌈ x/3 ⌉, z = 9b +⌈ y/3 ⌉, s = 9a +⌈ z/3 ⌉.
Es folgt durch sukzessives Einsetzen s = 9a + 3b + c + 1 = x.
Vorgehen, wenn die zuschauende Person von Anfang an einen Rang wählt, z.B. Rang 12:
Wir verwandeln 12-1 = 11 ins Dreiersystem: 102. Das bedeutet für die drei Phasen:
Phase 1: "2=unten", Phase 2: "0=oben", Phase 3: "1=Mitte".
Die gemerkte Karte wird dann auf Rang 12 landen.
Ursprüngliche Anordnung: 1, 2, 3, 4, 5, 6, 7, 8, 9 (Karten am besten mit Rückseite oben)
2 Stapel:
9
7 8
5 6
3
4
1 2
Aufnahme von rechts nach links (R-Variante). Neue Reihenfolge:
9 7 5 3 1 8 6 4 2
Tabelle der Rangveränderung:
| alter Rang | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| neuer Rang nach einem Durchgang | 5 | 9 | 4 | 8 | 3 | 7 | 2 | 6 | 1 |
Die neuen Ränge bilden eine arithmetische Folge modulo 9 (immer +4 von Feld zu Feld).
Die Formel, die dem alten Rang x den neuen Rang y zuordnet, ist also eine lineare Funktion und lautet:
y = 4x + 1 modulo 9 (Rang 9 belassen wir als 9, die übrigen Zahlen reduzieren wir auf ihre Neunerreste.)
Wenden wir diese Formel drei Mal an:
x ↦ 4x + 1 ↦ 4(4x + 1)+1 = 7x + 5 mod 9 ↦ 4(7x + 5)+1 = x + 3 mod 9.
Das bedeutet:
Rang x geht auf Rang x + 3, d.h. alle Ränge sind wieder in der ursprünglichen Ordnung, einfach noch zyklisch verschoben.
Das hängt damit zusammen, dass 4⋅4⋅4 = 1 mod 9 ist.
Übrigens entsteht die Steigung 4 in der Formel y = 4x + 1 wegen der Höhe 4 des rechten Teilstapels:
4 = (9 - 1)/2.
9 - 1 muss also durch die Anzahl Teilstapel (hier 2) teilbar sein.
Warum funktioniert der Ordnungstrick auch, wenn die Zuschauerin im Zweistapelspiel jedes Mal frei entscheiden kann, welcher der beiden Teilstapel obenauf kommt?
Das funktioniert deshalb, weil das bei nur zwei Stapeln einfach einem "Abheben" entspricht. Man kann nach jeder Phase des Spiels frei abheben: Dies verändert die Kartenordnung nicht, sondern verschiebt sie nur zyklisch. Bei mehr als zwei Stapeln geht dies nicht mehr.
13 Karten und 4 Teilstapel:
Teilstapel:
13
9 10 11 12
5 6 7 8
1 2 3 4
Neuer Gesamtstapel (von rechts nach links aufgestapelt):
13 9 5 1 10 6 2 11 7 3 12 8 4
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| y | 4 | 7 | 10 | 13 | 3 | 6 | 9 | 12 | 2 | 5 | 8 | 11 | 1 |
Die neuen Ränge bilden wieder eine arithmetische Folge modulo 13 (immer +3 von Feld zu Feld).
Formel alter Rang x ↦ neuer Rang y:
y = 3x + 1 mod 13 (mit Ausnahme von Rang 13).
Die Steigung 3 bedeutet auch die Anzahl Stockwerke in den Stapeln 2 bis 4.
3 = (13-1)/4.
Wegen 3⋅3⋅3 = 1 mod 13 ist nach 3 Durchgängen wieder die alte Ordnung hergestellt, allenfalls zyklisch verschoben.
13 Karten und 5 Teilstapel:
Hier entsteht keine formelkonforme Ordnung, denn (13-1)/5 ist keine natürliche Zahl.
Die neuen Ränge nach einem Durchgang bilden keine arithmetische Folge mehr.
Bemerkung: Werden die Ränge und die Kartenwerte statt von 1 bis n von 0 bis n-1 gezählt, wird die Sache mathematisch etwas einfacher, da man dann durchwegs modulo n (n = Anzahl Karten) rechnen kann.
6 7 8 9
1 2 3 4 5
Neue Reihenfolge:
5 9 4 8 3 7 2 6 1
Ränge vorher (x) und nachher (y):
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 9 | 7 | 5 | 3 | 1 | 8 | 6 | 4 | 2 |
Es entsteht eine arithmetische Folge modulo 9 (-2 von Feld zu Feld).
2 ist die Stockwerkhöhe der Teilstapel mit Ausnahme des Stapels ganz rechts.
2 = (9 + 1)/5. (-2 erscheint als Steigung der linearen Funktion.)
Die Anzahl Teilstapel muss ein Teiler von n+1 sein.
Lineare Funktion: y = -2x
-7 mod 9 oder äquivalent y = 7x + 2 mod 9.
(-2)⋅(-2)⋅(-2) = -8 = 1 mod 9: Nach 3 Durchgängen ist die Ordnung wieder hergestellt.
Ganz gekonnt wird es natürlich, wenn man R- und L-Variante mischt. Der Trick wird dann noch undurchsichtiger, besonders wenn das Aufstapeln schnell vor sich geht.
Bedingungen, wenn R- und L-Variante zum Zug kommen sollen:
Die Anzahl Teilstapel für die R-Variante muss ein Teiler von n-1 sein und
die Anzahl Teilstapel für die L-Variante muss ein Teiler von n+1 sein.
Das Produkt aller Steigungen der involvierten linearen Funktionen muss kongruent -1 oder 1 modulo n sein.
Zudem sollten nicht allzu viele Durchgänge nötig sein, sonst wird der Trick langatmig.

Für eine Pyramide mit den vier Zeilen 0 bis m = 3 klappt die Sache modulo 3, denn die Binomialkoeffizienten 3 in der unteren Spitze der Pyramide sind ja modulo 3 gleich 0 und alle mittleren Binomialkoeffizienten in der Summe verschwinden; es bleiben nur die äussersten Summanden bestehen. Die oberste Zeile besteht aus m + 1 = 4 Kästchen.
Man kann den Wert des untersten Spitzenfeldes in obiger Pyramide direkt aus den rot markierten Randwerten der obersten Zeile berechnen ohne die übrigen Zeilen auszufüllen.
Diese Tatsache liefert übrigens einen schönen Beweis für folgenden
Satz: Alle Binomialkoeffizienten der Form
(3r tief k), 1 ≤ k ≤ 3r-1, r ∈ ℕ \ {0}, sind gleich 0 modulo 3, d.h. sind durch 3 teilbar. Dies gilt übrigens nicht nur für die Primzahl 3, sondern für alle Primzahlen p (modulo p).
(Die Beweisüberlegung ist in der rechten Spalte ausgeführt.)
Illustration zu obigem Satz: Das Pascalsche Dreieck modulo 3:
Bildquelle: hier.
Binomialkoeffizienten modulo 3. Schwarz: Werte 0 mod 3.
Genau die Zeilen mit Zeilennummern der Form
3r, r ∈ℕ \ {0}, haben die Eigenschaft, dass alle Nichtrand-Binomialkoeffizienten gleich 0 modulo 3 sind. Das Analoge gilt für alle Primzahlen p (modulo p).
Das Bild zeigt schön, dass z.B. in Zeile 18 (18 ist keine Dreierpotenz!) der Binomialkoeffizient
(18 tief 9) nicht durch 3 teilbar ist.

Warum
? Die Bruchfaktoren 2 bis 9 oben lauten: (18-c ) / (9-c ), 1 ≤ c ≤ 8 . Zähler und Nenner haben je gleich viele Faktoren 3, nämlich so viele, wie c besitzt; sie kürzen sich alle heraus. Im ersten Bruchfaktor kürzen sich alle Faktoren 3 ebenfalls vollständig heraus.
Modulo-3-Rechnung in der Pyramide mit Zeilen 0 bis 9:
Die gelben Felder bilden für sich genommen wieder eine Pyramide mit Zeilen 0 bis 3, die das Bildungsgesetz (unterliegendes gelbes Feld = Summe der beiden darüberliegenden gelben Felder) respektiert, so dass die gelbe Spitze unten gemäss den Überlegungen links den Wert x1
+ x10 annimmt.
Wie kamen wir von der Pyramide mit Zeilen 0 bis 3 zur Pyramide mit Zeilen 0 bis 9? Wir haben drei kleine Pyramiden mit je einem Feld Überlappung aneinandergereiht und die Figur wieder zu einer kopfstehenden Pyramide ergänzt. Diese neue Pyramide hat die Zeilen 0 bis 32 = 9. Die Grundzeile hat 32 + 1 Kästchen.


Analog kann man weiterfahren und aus
der Pyramide mit den Zeilen 0 bis m = 9 eine grössere mit den Zeilen 0 bis m = 27 herstellen, dann eine mit den Zeilen 0 bis m = 81, usw.
m ist also stets eine Dreierpotenz.
Somit klappt die Sache sicher mit allen m der Form m = 3r, r ∈ ℕ \ {0} bzw. für alle Pyramiden, die in der Grundzeile 3r + 1 Kästchen haben.
Man kann diese Überlegung etwas exakter als Induktionsbeweis führen: s. hier (PDF).
Unsere Überlegung mit obiger Pyramide zeigt, dass alle Binomialkoeffizienten der Form (3r tief k) für 1 ≤ k ≤ 3r-1, r ∈ ℕ \ {0}, gleich 0 modulo 3, d.h. durch 3 teilbar sind. Die Überlegung gilt nicht nur für p = 3, sondern für alle Primzahlen p: Jede Primzahl p teilt (p tief k) für 1 ≤ k ≤ p-1. Nach obiger Überlegung teilt dann auch pr alle Binomialkoeffizienten (pr tief k) für 1 ≤ k ≤ pr-1.
Behauptung: Wir zeigen, dass im Pascalschen Dreieck genau die Zeilen mit Zeilennummer 3r , r ∈ℕ \ {0}, die Eigenschaft haben, dass die Nichtrand-Binomialkoeffizienten modulo 3 gleich 0 sind (Zeilennummerierung beginnt bei 0). Die Überlegung gilt analog für beliebige Primzahlen p (modulo p). Das Bild links illustriert diesen Satz.
Zunächst ist festzustellen, dass wir nur Zeilen mit einer durch 3 teilbaren Zeilennummer m betrachten müssen, denn (m tief 1) = m ist eine Nichtrand-Zahl und soll modulo 3 null, also durch 3 teilbar sein. Auch dies zeigt sich schön im Bild links.
Sei m = a⋅3r, r maximal, d.h. a und 3 sind teilerfremd. Wir werden zeigen: a = 1, womit die Behauptung bewiesen ist.
Annahme: a > 1:
Wir behaupten: (a⋅3r tief 3r ) (das ist wegen a > 1 ein Nichtrand-Binomialkoeffizient) ist nicht durch 3 teilbar, also ≠0 modulo 3.
Es gilt: a⋅3r- c und 3r - c, c ∈ ℕ, 1 ≤ c ≤ 3r-1, haben in der Primfaktorzerlegung gleich viele Faktoren 3, nämlich so viele wie die Zahl c besitzt.
Begründung: 3r enthält die "Maximaldosis" an Faktoren 3. In der Differenz mit c ist der grösste gemeinsame Teiler enthalten; dieser enthält nur noch so viele Faktoren 3 wie c sie hat, sofern c ≤ 3r-1.
Beispiel: a = 5, r = 2:
45 - 1 hat 0 Faktoren 3, weil 1 ebenfalls 0 Faktoren 3 hat; 45 - 3 hat einen Faktor 3, weil 3 einen Faktor 3 hat; 45 - 6 hat einen Faktor 3, weil 6 nur einen hat.
Damit haben in der ausgeschriebenen Definition von

in jedem der Bruchfaktoren Zähler und Nenner gleich viele Faktoren 3, die sich alle wegkürzen, denn auch das zu 3 teilerfremde a enthält keinen Faktor 3. Somit ist 3 kein Teiler von (a⋅3r tief 3r ). Folglich muss für Zeilen, in denen alle Nichtrand-Binomialkoeffizienten = 0 modulo 3 sind, a = 1 sein und die Zeilennummer ist von der Form 3r.
Beispiel für a = 5 und r = 2:
(45 tief 9) = (45 / 9)⋅(44 / 8)⋅(43 / 7)⋅(42 / 6 )⋅(41 / 5)⋅(49 / 4 )⋅(39 / 3)⋅(38 / 2)⋅(37 / 1) =
(5 / 1)⋅(44 / 8)⋅(43 / 7)⋅(14 / 2)⋅(41 / 5)⋅(49 / 4)⋅(13 / 1)⋅(38 / 2)⋅(37 / 1).
Sämtliche Faktoren 3 haben sich weggekürzt und somit ist (45 tief 9) nicht durch 3 teilbar.
Dieser Beweis gilt nicht nur für p = 3, sondern für alle Primzahlen, wenn modulo p gerechnet wird.
Hier ein PDF mit dem Beweis zu obigem Satz und einem Korollar dazu.
Wie diese Theorie in den magischen Trick umgewandelt wird, zeigt dieses PDF.
Es werden kleine Rechteckkarten in 3 Farben benötigt. Anstelle unserer Restklassenzahlen modulo 3 (0, 1, 2) setzen wir die Farben, z.B. 0 = rot, 1 = blau, 2 = gelb.
Als oberste Zeile der Pyramide werden 10 Karten in beliebiger Reihenfolge gelegt.
Bildungsgesetz:
Die nächst unteren Zeilen werden wie folgt gebildet: Sind über einem Feld zwei Karten gleicher Farbe, erhält das Feld darunter ebenfalls diese Farbe. Sind über einem Feld zwei Karten ungleicher Farbe, erhält das Feld darunter die dritte Farbe.
Diese Regel entspricht folgender Zuordnungsfunktion:
(0, 0) ↦ 0; (0, 1) ↦ 2; (0, 2) ↦ 1; (1, 0) ↦ 2; (1, 1) ↦ 1; (1, 2) ↦ 0; (2, 0) ↦ 1; (2, 1) ↦ 0; (2, 2) ↦ 2.
Diese Funktion wird gewährleistet durch folgende Regel:
Seien a und b die Werte der beiden Felder, die über einem Feld der nächst unteren Zeile liegen. Dann ist der Wert dieses darunter liegenden Feldes gleich (-a) + (-b) = -a - b = -(a + b) modulo 3.
Es entstehen dieselben Binomialkoeffizienten wie oben beschrieben und folglich funktioniert die Sache gleich wie oben.
Eine Person legt 10 Farbkarten (Sorten Rot, Blau, Gelb) in beliebiger Auswahl nebeneinander hin. Die Magierin kann sofort die Farbe der Spitze vorhersagen, wenn die kopfstehende Pyramide nach den Regeln oben aufgebaut wird (sie muss nur die Eckkarten der obersten Zeile 0 beachten).- Wie der Trick noch magischer gestaltet werden kann, wird im Buch von Ehrhard Behrends: Mathematik und Zaubern beschrieben.
Auch werden dort Varianten beschrieben, die z.B. mit Spielkarten Rot und Schwarz und Binomialkoeffizienten modulo p=2 durchgeführt werden können.
Für p = 2 lauten die passenden Pyramidenhöhen 2r +1, also 3, 5, 9, ... Sei 0=rot und 1=schwarz. Man erfinde eine Lege-Regel, die der Funktion (a, b) ↦ a+b mod 2 entspricht.

Ein Beispiel mit n:= m+1 = 10. Die Farbe an der Pyramidenspitze ganz unten hängt lediglich von den beiden Randfeldern der obersten Zeile ab. Funktion: (a, b) ↦ -(a + b) mod 3.
Im Bild oben sind z.B. die Randfelder von Zeile 0 gelb und rot; die untere Spitze wird somit gemäss dem links beschriebenen Bildungsgesetz blau.
Sind nicht genügend Farbkarten vorhanden, können nach einer Weile ein paar obere Zeilen abgebaut werden. Die Sache wird dann noch undurchsichtiger.
Noch geheimnisvoller wird die Sache, wenn die Magierin bereits vor dem Legen der obersten Zeile ihre Vorhersage in einem Couvert deponiert. Nach dem Legen der obersten Zeile dürfen dann die Zuschauerin und anschliessend die Magierin noch Veränderungen an der Zeile anbringen. Die Magierin wählt dann natürlich die passenden Eckwerte.


| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Summe mod 100 |
| x8 mod 100 | 0 | 1 | 56 | 61 | 36 | 25 | 16 | 1 | 16 | 21 | 33 |
Sei n ≥ m, andernfalls vertausche man die ai und die bj.
Als weitere Voraussetzung fordern wir 1 ≤ a < n. Für a = 0 wird N = mn, für a ≥ n wird N = 0.
Sei N die Anzahl der gesuchten Punkte P(i, j) mit | i - j | ≥ a.
Sei M:= min(m, n-a)
Sei L: = min(m, a)
Die Formel für N findet sich im grünen Kasten rechts. Man prüfe sie an den Beispielen nach.
Der erste Summand der Formel gibt die Anzahl Punkte oben links an, der zweite die Anzahl Punkte unten rechts.
Beispiele 1 - 4: m = 4, n = 7:


Beispiel 1: m = 4, n = 7, a = 1, M = 4, L = 1 => N = 6 + 18 = 24
Beispiel 2: m = 4, n = 7, a = 2, M = 4, L = 2 => N = 3 + 14 = 17
Beispiel 3: m = 4, n = 7, a = 4, M = 3, L = 4 => N = 0 + 6 = 6
Beispiel 4: m = 4, n = 7, a = 5, M = 2, L = 4 => N = 0 + 3 = 3
Lösung Zusatzaufgabe m = 50, n = 60, a = 30, M = 30, L = 30 =>
N = 20
⋅21 / 2 + 31⋅30 / 2 = 210 + 465 = 675, das sind 22.5% aller Punkte des Rasters.
Beispiel 5: m = 6, n = 7, a = 3, M = 4, L = 3 => N = 6 + 10 = 16

Beispiel 6: m = 3, n = 7, a = 3, M = 3, L = 3 => N = 0 + 9 = 9

Sei ohne Beschränkung der Allgemeinheit n ≥ m. Hier die Formel für N in Abhängigkeit von m, n und a:
 |
Durch die Definition von M und L als min(m ; n-a) bzw. min(m; a) können lästige Fallunterscheidungen umgangen werden.
Folgende Fallunterscheidungen sind jedoch trotzdem nötig:
Die Formel gilt nicht für a = 0 (N = mn) und a > n (N = 0). (Für a = n liefert die Formel noch N = 0.)
Für a = 0 zählt die Formel die m Punkte P(i, i) leider doppelt.
Annahme: Keine der n Summenzahlen si sei durch n teilbar, d.h. bei Division durch n entstehe immer ein Rest. Wir erhalten n solche Reste, die wir den n - 1 "Restschubladen" 1, ... , n-1 zuordnen (die Schublade "Rest 0" existiert ja nach Annahme nicht).
Nach dem Schubfachprinzip gibt es somit eine Schublade, die mindestens zwei Summenzahlen mit gleichem Rest enthält. (Wenn wir n Dinge in n-1 Schubladen versorgen, muss es mindestens eine Schublade geben, die mehr als 1 Ding enthält.)
Seien diese zwei Summenzahlen mit gleichem Rest si und sk. Sei si < sk.
Wir bilden sk - si . Diese Zahl hat bei Division durch n dann natürlich Rest 0.
Es ist sk - si = (1 + z + ... + zi + zi+1 + ... + zk ) - (1 + z + ... + zi )
= zi+1 + ... + zk.
Wir klammern zi+1 aus: zi+1(1 + ... + zk-i-1 ) = zi+1⋅sk-i-1.
n teilt diese Zahl, aber da n teilerfremd zu z ist, teilt n den Faktor zi+1 nicht, sondern teilt den andern Faktor, sk-i-1, d.h eine der Summenzahlen, was im Widerspruch zu unserer Annahme steht, dass n keine der Summenzahlen teilt.
Folglich ist die Annahme, dass n keine der Summenzahlen teilt, falsch, und n teilt mindestens eine der Summenzahlen.

Die Annäherung kann noch weiter verbessert werden (bis etwas unter 1.2021).
Das Vorgehen mit der exponentiell wachsenden Klammerung wird Verdichtung der Reihe genannt. Jede Klammersumme wird nach oben abgeschätzt, indem alle Summanden einer Klammer durch den ersten, grössten Summanden ersetzt werden. Dadurch entsteht eine geometrische Reihe, die für |q| < 1 konvergiert.
Diese geometrische Reihe ist eine Majorante gegenüber der ursprünglichen Reihe (beide Reihen bestehen nur aus positiven Elementen).
Im Gegensatz zur einfachen harmonischen Reihe 1 + 1/2 + 1/3 + ..., die divergiert, konvergiert somit die verallgemeinerte harmonische Reihe.
Hier nochmals die definierenden Bedingungen für f(x, y):
- f(0, y) = y + 1
- f(x+1, 0) = f(x, 1)
- f(x+1, y+1) = f(x, f(x+1, y))
Aus (1) ergibt sich sofort die erste Spalte mit x = 0.
Die Funktionswerte dieser Spalte (rot eingetragen) berechnen sich
zu
(*):
f(0, y) = y+1.

Aus (2) ergibt sich f(1, 0) = f(0, 1) = 2.
Aus (3) folgt f(1, y+1) = f(0, f(1,y)) = f(1, y) + 1 (letzte Gleichheit nach (*))
So ergibt sich die zweite Spalte (x = 1): Start bei 2, nach oben immer +1,
d.h. f(1, y) = y + 2.

Aus (2) ergibt sich f(2, 0) = f(1, 1) = 3.
Aus (3) folgt f(2, y+1) = f(1, f(2,y)) = f(2, y) + 2
(letzte Gleichheit nach dem Gesetz der zweiten Spalte (x= 1): f(1, y) = y + 2).
So ergibt sich die dritte Spalte (x = 2): Start bei 3, nach oben immer + 2,
d.h. f(2, y) = 2y + 3 (siehe nächste Abbildung links).


Nun zur 4. Spalte (x = 3): Es ist f(3, 0) = f(2, 1) = 5.
f(3, y +1) = f(2, f(3,y)) = 2⋅f(3,y) + 3.
Damit ergibt sich die 4.Spalte (x = 3): Start bei 5; nach oben immer "mal 2 plus 3".
Welche Funktion könnte dieser Zahlfolge entsprechen (rotes Fragezeichen oben)?
"mal 2" deutet auf eine Exponentialfunktion mit Basis 2 hin. Wir probieren folgenden Ansatz:
f(3, y) = a⋅2y + b. Setzen wir die y-Werte 5 und 13 ein, ergibt sich:
5 = a + b und 13 = 2a + b. Daraus folgt a = 8 und b = -3 und die Funktion lautet:
f(3, y) = 8⋅2y - 3 = 2y+3 - 3.
Diese Funktion erzeugt tatsächlich die Spaltenwerte oben, und es lässt sich sofort zeigen, dass beim Übergang von y zu y + 1 der neue Funktionswert aus dem alten hervorgeht, indem man "mal 2 plus 3" rechnet.
5. Spalte (x =4): f(4, 0) = f(3, 1) = 13 (Bild oben rechts).
f(4, y + 1) = f(3, f(4, y)) =
8⋅2f(4, y) - 3; Startwert für y=0 ist 13. Es folgt:
f(4, 1) =
8⋅213 - 3 = 65'533. f(5, 0) = f(4, 1) ist ebenfalls 65'533.
f(4, 2) = 8⋅265533 - 3: eine riesige Zahl in der Grössenordnung 2⋅1019728.
Zum Vergleich: Die Anzahl Atome im gesamten Universum wird auf "nur" 1089 geschätzt!
Die Funktionswerte im Gitter wachsen explosionsartig an.
Wer will, kann noch die Funktionsvorschrift für f(4, y) suchen (da kommen wir bereits ins "Hyperpotenzieren" und benötigen Potenztürme, sowie Und-so-weiter-Pünktchen ... ).
Es ist z.B. f(4, 3) = 2^2^2^16 - 3 = 2^2^2^2^2^2 - 3 (6-mal eine 2)
f(4, 4) = 2^2^2^2^2^2^2 - 3 (7-mal eine 2)
f(4, y) = 2^2^...^2 -3 (y+3 - mal eine 2)
Die Potenztürme klammern von rechts nach links, was ein unglaubliches Wachstum ergibt!
Betrachten wir abschliessend noch f(5,1):
f(5, 1) = f(4, f(5,0)) = f(4, 65533) = 2^2^...^2 - 3 (216-mal eine 2, d.h. 65'536-mal eine 2).
Die normale Exponentenschreibweise lässt eine Verallgemeinerung nicht zu. Stattdessen wird häufig die Pfeilschreibweise von Knuth verwendet (siehe Anhang unten).
Die Gitterwerte ab x = 4 explodieren förmlich, was man der harmlosen Definition von f(x, y) anfänglich gar nicht ansieht!
Die Funktion f(x, y), aber auch z.B. f(x, 0) mit der Wertefolge 1, 2, 3, 5, 13, 65533, ...führen ins Gebiet der Ackermann-Funktionen (siehe auch hier in OEIS). Diese Funktionen führen in die Grundlagen der Mathematik; es sind berechenbare, aber nicht primitiv-rekursive Funktionen.
Die Folge der Diagonaleinträge f(x, x) des Gitters oben, 1, 3, 7, 61, ..., gehört ebenfalls zu den Ackermann-Folgen.
Unsere zunächst harmlos anmutende Funktion f(x, y), die 1935 von der Mathematikerin Rózsa Péter beschrieben wurde, vereint in sich eine ganze unendliche Schar immer schneller wachsender Funktionen. In jeder Spalte entsteht eine neue Funktion; zunächst haben wir lineares Wachstum (x = 0 bis 2), dann exponentielles (x = 3), dann hyperexponentielles, usw.
Anhang zur Aufgabe: Pfeilschreibweise von Knuth
Die normale Potenzschreibweise lässt sich nicht mehr verallgemeinern. Eine Verallgemeinerung ist jedoch möglich mittels der Pfeilschreibweise von Knuth.
Es werden Mehrfachpfeile nach oben verwendet: ↑↑↑ = ↑3, usw.
↑ ist die gewöhnliche Potenzierung; ↑↑ wird Tetration genannt.
a ↑0 b = a⋅b a ↑1 b = ab a ↑2 b = a ↑1 a ↑1 ... ↑1 a (b Buchstaben a) = a^a^a^...^a (b Buchstaben a) a ↑3 b = a ↑2 a ↑2 ... ↑2 a (b Buchstaben a) usw. |
Die Ketten werden von rechts nach links aufgelöst.
Mit Hilfe dieser Notation kann der Raster mit der Funktion oben klarer definiert werden:
f(1, y) = [2 ↑-1 (y+3)] - 3= 2+(y+3)-3 = y+2 wie gehabt.
f(2, y) = [2 ↑0 (y+3)] - 3= 2⋅(y+3)-3 = 2y+3 wie gehabt.
f(3, y) = [2 ↑1 (y+3)] - 3= 2y+3 - 3 wie gehabt.
f(4, y) = [2 ↑2 (y+3)] - 3 = 2^2^...^2 - 3 (y+3-mal eine 2) wie gehabt.
f(5, y) = [2 ↑3 (y+3)] - 3
...
| f(x, y) = [2 ↑x-2 (y+3)] - 3 |
Damit gelingt eine einheitliche Formulierung für f(x, y).
Da hier immer höhere (von x abhängige) Pfeiloperationen
↑x-2 auftreten, die in einem Computerprogramm immer mehr ineinander verschachtelte Loops benötigen, ist die gesamte Ackermannfunktion nicht "loop-berechenbar", d.h. nicht rekursiv-primitiv (die Ackermannfunktion beinhaltet Operationsstufen beliebiger Höhe).
Jedoch ist für gegebenes x, y der Wert f(x, y) (im Rahmen der Fähigkeit des Computers) berechenbar.
Beispiele:
f(5, 1) = [2 ↑3 4)] - 3 = [2 ↑2 2 ↑2 2 ↑2 2] - 3 =
[2 ↑2 2 ↑2 22] - 3 = [2 ↑2 2 ↑2 4] - 3 = [2 ↑2 (2^2^2^2)] - 3 =
[2 ↑2 65'536] - 3 = [2^2^...^2] - 3 (65'536-mal die 2): jenseits unserer Vorstellungskraft!
f(4, 4) = 2 ↑2 7 - 3 = 2^...^2 - 3 (7-mal die 2) = 2^(2^(2^65'536)) - 3:
eine unvorstellbar grosse Zahl!
Anhang 2: LOOP-Programme
Bei einem LOOP-Programm ist bereits vor dem Durchlaufen eines Loops festgelegt, wie oft dieser realisiert werden soll.
Im Gegensatz dazu wird bei einem WHILE-Programm ein Loop so lange durchlaufen, wie eine bestimmte Variable ≠ 0 ist. Deshalb ist es in einem WHILE-Programm theoretisch möglich, dass ein Loop endlos absolviert wird, das Programm somit nie endet, während dies in einem LOOP-Programm nicht vorkommt: Ein LOOP-Programm terminiert stets nach endlich vielen Schritten.
Unsere Ackermannfunktion f(x, y) oben lässt sich nicht als LOOP-Programm formalisieren, denn diese Funktion hat, wie oben gezeigt, die "seltsame" Eigenschaft, dass die Funktionsgleichung, d.h. die durchzuführende Operation
f(x, y) = [2 ↑x-2 (y+3)] - 3,
vom Argument x abhängig ist:
Die Funktionsgleichung wandelt sich in eine solche höherer Stufe, wenn x sich verändert!
In einem LOOP-Programm hiesse dies, dass immer mehr ineinander verschachtelte Loops entstünden, d.h. dass sich das Programm mit wandelndem x ebenfalls verändern müsste. Die Ackermannfunktion ist nicht LOOP-programmierbar, jedoch durchaus berechenbar.
Schema verschachtelter Loops für die Potenzierung zweier Zahlen:

Für höhere Operationen (Tetration, usw.) würden immer mehr Verschachtelungen benötigt.
Beispiel:

Belegung der Variablen Schritt für Schritt:
| x0 |
1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 8 |
| x3 |
0 | 1 | 2 | 0 | 1 | 2 | 3 | 4 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 8 |
hellblau: Definition bzw. Neudefinition x0 und Reset x3 auf 0 nach äusserstem Loop
+1-Schritte: innerster Loop (x0-mal)
violett: Wiederholung infolge des mittleren Loops
Gesucht sind 100-stellige Harshad-Zahlen n, also Zahlen, die durch ihre Quersumme teilbar sind.
Die Ziffer 0 soll nicht vorkommen.
1. Quersumme 125:
Die Zahl aus den letzten 3 Ziffern muss durch 125 teilbar sein.
Ein mögliches n ist z.B. 1...14444443125 (vorne 90-mal eine 1).
2. Quersumme 144:
Die Zahl n muss durch 9 und durch 16 teilbar sein. Mit Quersumme 144 ist sie durch 9 teilbar; die Zahl aus den letzten 4 Ziffern muss durch 16 teilbar sein.
Ein mögliches n ist z.B. 1...15555554848 (vorne 90-mal eine 1).
3. Quersumme 128:
Die Zahl n muss so sein, dass die Zahl gebildet aus den hinteren 7 Ziffern durch 128 teilbar ist.
Ein mögliches n unter vielen andern ist z.B. 1...13331563392 (vorne 90-mal eine 1).
4. Quersumme 108:
Die Zahl n muss durch 27 und durch 4 teilbar sein. Das bedeutet: Die Quersumme von n muss durch 9 teilbar sein und die Quersumme von n/9 muss durch 3 teilbar sein, zudem muss die Zahl gebildet aus den letzten beiden Ziffern durch 4 teilbar sein.
Ein mögliches n ist z.B. die Zahl mit der Ziffernfolge
(111111111)...(111111111)(1111111524) (10-mal die blaue Klammer).
(Achtung: Die Klammern bedeuten keine Multiplikation; sie dienen nur der Gliederung der Ziffernfolge!)
Die Quersumme stimmt bereits; n ist also durch 9 teilbar. Ebenso ist n wegen der Endung 24 durch 4 teilbar. Wir müssen noch n/9 prüfen.
n/9 = (012345679)...(012345679)(0123456836) (10-mal die grüne Klammer)
Die Quersumme von n/9 ist 10⋅37+38 = 408, also eine Dreierzahl, folglich ist n/9 ebenfalls durch 3 teilbar.
Damit ist gezeigt, dass dieses n durch 108 teilbar ist.
Ein anderes mögliches n wäre z.B.
(111111111)...(111111111)(1111111416) (10-mal die blaue Klammer).
Oder auch:
(111111111)...(111111111)(1111111632) (10-mal die blaue Klammer).
Gibt es eine direkte Teilbarkeitsregel für 27?
Eine direkte Teilbarkeitsregel für 27 würde uns die Überlegung oben (rechte Spalte) mit n/9 ersparen. Wir gewinnen eine solche Regel durch folgende Überlegung:
1:27 ergibt Rest 1; 10 : 27 ergibt Rest 10; 100 : 27 ergibt Rest 19, 1000 : 27 ergibt wieder Rest 1, usw.
Wir multiplizieren somit von hinten nach vorn die Ziffern der Reihe nach mit
1, 10, 19, 1, 10, 19, usw. Ist das Ergebnis durch 27 teilbar, ist es auch die Zahl.
Angewendet auf obiges
n = 1...1524 (vorn 97 Einsen) gliedern wir die Ziffern also von hinten her in Dreiergruppen:
n = 1(111)...(111)524 [32 (111)-Klammern].
Die Klammern bedeuten wiederum keine Multiplikation, sondern gliedern lediglich die Ziffern.
Unsere 27er-Regel ergibt dann
1⋅1+(19⋅1+10⋅1+1⋅1)+...+(19⋅1+10⋅1+1⋅1)+19⋅5+10⋅2+1⋅4 = 1+32⋅30+119 = 1080, was durch 27 teilbar ist. Somit ist unsere Zahl n durch 27 teilbar.
Die zweistellige Zahl sei 10x+y, die einstellige sei z.
Das Produkt wird dann gleich 10xz+yz. Für die Addition unterscheiden wir 3 Fälle:

Fall 1: Das Resultat der Addition ist dreistellig: x = 9, y+z ≥ 10 (Bild oben links).
Die Umkehrzahl der Addition und damit das Resultat der Multiplikation muss dann hinten eine 1 haben. In Frage kommen dann nur 99*9, 93*7 und 97*3. Diese Zahlen zeigen das gesuchte Phänomen nicht. Fall 1 scheidet aus.
Fall 2: y+z≥10, Resultat jedoch zweistellig.
Die Umkehrzahl der Addition lautet dann 10(y+z-10)+x+1 = 10y+10z+x-99.
Die Gleichung "Umkehrzahl = (10x+y)z" lautet: 10y+10z+x-99 = 10xz+yz oder
(10-z)y=99+10z(x-1)-x. Die rechte Seite wird für jede Wahl von x grösser als 90 (man beachte: 9≥x>0), die linke Seite kann jedoch höchstens gleich 81 werden. Fall 2 scheidet ebenfalls aus.
Fall 3: y+z ≤ 9, d.h. kein Übertrag bei der Addition.
Die Umkehrzahl der Addition lautet dann 10(y+z)+x = 10y+10z+x.
Die Gleichung "Umkehrzahl = (10x+y)z" lautet: 10y+10z+x = 10xz+yz.
Wir probieren z-Werte von 1 bis 9 durch.
Beispiel: z = 1: 10y+10+x=10x+y oder 9y+10=9x. Das kann aus Teilbarkeitsgründen nicht sein.
Wir finden hier jedoch für z = 2 und für z = 3 Lösungen:
z = 2: 10y+20+x = 20x+2y oder 8y
+20=19x => y = 7 und x = 4.
Lösung 1: 47+2=49; 47*2=94.
z=3: 10y+30+x=30x+3y oder 7y+30
= 29x => y = 4 und x = 2.
Lösung 2: 24+3=27; 24*3=72.
Alle andern z-Werte ergeben keine weiteren Lösungen.
Sei r7 der Rest bei Division durch 7, r5 der Rest bei Division durch 5 und r3 der Rest bei Division durch 3.
Sei x die gesuchte Zahl.
(1): x ist kongruent r7 mod 7
(2): x ist kongruent
r5 mod 5
(3): x ist kongruent r3 mod 3
Wir finden in z:=15r7-14r5 eine Zahl, welche (1) und (2) gleichzeitig erfüllt.
Begründung:
Das funktioniert wegen 1 = 3*5 - 2*7.
(5 und 7 haben als teilerfremde Zahlen ggT 1, der sich als Linearkombination aus 5 und 7 darstellen lässt.)
Somit:
(*):
15 ist Vielfaches von 5 und gleichzeitig kongruent 1 mod 7 und -14 ist Vielfaches von 7 und gleichzeitig kongruent 1 mod 5. Es folgt:
z =15r7-14r5 ist kongruent 15r7 mod 7, d.h. nach (*) auch kongruent r7 mod 7.
z =15r7-14r5 ist zudem kongruent -14r5 mod 5, d.h. nach (*) auch kongruent r5 mod 5.
z erfüllt somit (1) und (2) gleichzeitig.
Sofern wir zu z ein Vielfaches von 35 addieren oder subtrahieren, erhalten wir neue Zahlen, die ebenfalls (1) und (2) gleichzeitig erfüllen. Das gesuchte x ist somit kongruent unserem z modulo 35.
Damit ist die Auswahl auf wenige Zahlen (zwei oder drei Zahlen) beschränkt. Daraus filtern wir nun noch die Zahl heraus, welche (3) erfüllt.
Ein Beispiel:
(1): x sei kongruent 1 mod 7
(2): x sei kongruent 2 mod 5
(3): x sei kongruent 2 mod 3.
z = 15*1 - 14*2 = -13.
x ist kongruent -13 mod 35 oder auch kongruent 22 mod 35.
Das heisst: x ist entweder 22, 57 oder 92; diese Zahlen erfüllen (1) und (2).
Gemäss (3) ist x somit gleich 92.
Bemerkung:
Unser Vorgehen entspricht dem Beweis im Chinesischen Restsatz.
Noch ein Beispiel:
(1): x sei kongruent 6 mod 7
(2): x sei kongruent 3 mod 5
(3): x sei kongruent 1 mod 3
z = 15*6 - 14*3 = 48.
x ist entweder 13, 48 oder 83; diese Zahlen erfüllen (1) und (2).
Gemäss (3) ist x somit gleich 13.
Ein einfacherer Lösungsweg ohne Theorie des Chinesischen Restsatzes
Wir haben mit der Theorie des Chinesischen Restsatzes ein wenig mit Kanonen auf Spatzen geschossen. Es geht auch einfacher:
1. Starte bei r7 und addiere so oft 7, bis du eine Zahl erreichst, die bei Division durch 5 den Rest r5 ergibt.
2. Prüfe
r3 nach und addiere allenfalls ein oder zwei Mal 35, bis auch r3 stimmt.
Beispiel mit r7 = 4, r5 = 2 und r3 = 1.
4; 11; 18; 25; 32. Die Zahl 32 erfüllt (1) und (2), nicht aber (3). 32+35 = 67 erfüllt auch (3).
Wir haben in der obigen ersten Lösung (1) und (2) durch eine neue Gleichung ersetzt. Wir wählten z:=15r7-14r5..
15 war kongruent 1 mod 7 und kongruent 0 mod 5, und -14 war kongruent 1 mod 5 und kongruent 0 mod 7.
Wir können analog ein neues z finden, das gleichzeitig (1), (2) und (3) erfüllt:
Der erste Faktor muss kongruent 1 mod 7 und gleichzeitig kongruent 0 mod 3 und mod 5 sein. Kandidat: 15.
Der zweite Faktor muss kongruent 1 mod 5 und gleichzeitig kongruent 0 mod 3 und mod 7 sein. Kandidat: 21.
Der dritte Faktor muss kongruent 1 mod 3 und gleichzeitig kongruent 0 mod 7 und mod 5 sein. Kandidat. 70.
Wir wählen somit z:=15r7+21r5+70r3.
Diese Zahl erfüllt (1), (2) und (3) gleichzeitig; aber auch alle Zahlen, die sich von z um ein Vielfaches von 105 unterscheiden, tun dies. Dies liefert uns die eindeutige Lösung zwischen 1 und 100.
Beispiel: r7 = 6, r5 = 4 und r3 = 1.
z=
90+84+70 = 244. Wir subtrahieren 210 und erhalten 34 als Lösung. Es ist die einzige Lösung im Bereich 1 bis 100, da wir modulo 105 rechnen.