Die Linie - ein mathematisch-kultureller Rundgang

Die rationalen und die reellen Zahlen und die Zahlengerade

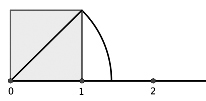
Die Entdeckung, dass die Diagonale eines Quadrates von Seitenlänge 1 keine rationale Längenmasszahl besitzt, war äusserst folgenreich. Bis heute beschäftigt Philosophen und Mathematiker das "Wesen" der reellen Zahlen.

Bild rechts: Obwohl die Brüche auf der Zahlengeraden unwahrscheinlich dicht nebeneinander liegen (zwischen zwei noch so nahe zusammenliegenden Brüchen gibt es stets noch unendlich viele dazwischenliegende), bringt es die gezeichnete Diagonale fertig, wenn sie nach unten gestürzt wird, in ein "Loch" zu fallen. √2 -die Masszahl dieser Diagonalen- ist irrational, d.h. kein Bruch.

Weiss man, dass sich jede natürliche Zahl bis auf Reihenfolge eindeutig in Primfaktoren zerlegen lässt, kann man rasch zeigen, dass die Länge x der Diagonalen im Quadrat mit Seitenlänge 1 keine Bruchzahl sein kann:

Wäre x eine Bruchzahl, so müsste nach dem Satz von Pythagoras gelten:

1² + 1² = x² oder

x² = 2.

Wäre x ein (gekürzter) Bruch m/n, so gälte also:

m²/n² = 2

oder

m² = 2 n²

Die linke Seite dieser Gleichung besteht aber (als Quadratzahl) aus einer geraden Anzahl Primfaktoren, die rechte Seite aber -wegen der zusätzlichen 2- aus einer ungeraden Anzahl Primfaktoren. Das kann nicht sein. Folglich kann x nicht Bruchform m/n haben.

Man erfindet für diese nichtrationale Zahl x ein neues Zeichen: √2.

Sokratischer Dialog über Brüche und Dezimalzahlen

Der berühmte Sokrates trifft in der Unterwelt Georg Cantor. Für einmal ist nun Sokrates der Schüler, der von Georg Cantor etwas über das "Unendliche" erfahren will.

Sokrates und Cantor in verblüffender Doppelkopf-Ähnlichkeit...

Der Mathematiker Georg Cantor zeigte, dass man die Bruchzahlen "auf einen Faden aufreihen", d.h. in eine abzählbare Reihenfolge bringen kann - natürlich nicht der Grösse nach. - Dann zeigte er, dass man die Menge der reellen Zahlen (zu der neben den Brüchen auch die nicht-rationalen Zahlen wie √2, √3 oder π gehören), nicht in eine solche abzählbare Auflistung bringen kann.

Diese Überlegungen seien hier im Stil eines sokratischen Dialoges vorgestellt, in einem fiktiven Dialog, wie ihn Plato in seinen Schriften verwendet hat, also als frei erfundenes Gespräch, das hier zwischen Sokrates (469 v.Chr. - 399 v. Chr) und Georg Cantor (1845 - 1918) stattfinden soll. In Wirklichkeit liegen zwischen dem Leben von Sokrates und demjenigen von Cantor über 2000 Jahre.

Anmerkung: Sokrates verwendet hier die Begriffe "Bruch", "Zähler", "Nenner". Als alter Grieche waren ihm diese Begriffe noch nicht bekannt, ebensowenig kannte der Dezimalbrüche (er hat also im Hades fleissig weiter Mathematik gebüffelt), stellten doch die alten Griechen Brüche immer als Verhältnisse a : b zweier ganzer Zahlen dar.

1

Sokrates: Sei gegrüsst, du Geistesverwandter! Froh bin ich, dich zu treffen, denn ich möchte gerne einiges über deine für mich noch verwirrenden Gedanken zum Unendlichen erfahren.

Georg Cantor: Es ist mir eine Ehre, mich mit dem berühmten Sokrates zu unterhalten. Was genau ist dein Anliegen?

Sokrates: Wie ich hörte, behauptest du zwei für mich erstaunliche und unverständliche Dinge. Erstens sagst du, könne man alle Brüche wie Perlen auf einer Schnur aufreihen und hintereinander aufzählen, so wie man das mit den natürlichen Zahlen 1, 2, 3,... tun kann. Wie soll das gehen?

Cantor: Warum zweifelst du daran, dass man die Brüche schön aufgereiht anordnen kann?

Sokrates: Wenn ich versuche, die Brüche aufzuzählen: Wie soll ich das denn tun? Jedesmal, wenn ich zwei Brüche hintereinander aufzähle, gibt es doch unendlich viele weitere Brüche dazwischen. Und wenn ich dann einige dieser Zwischenbrüche aufzähle, finden sich dazwischen wieder unendlich viele weitere. Ein Bruch hat ja nicht einen Nachbar-Bruch wie das bei den natürlichen Zahlen der Fall ist. Ich kann zwei eng benachbarte Brüche wählen, aber dazwischen liegen dann noch ganze Bündel weiterer Brüche und dazwischen wieder weitere Bündel. Bündel über Bündel. Und diese dicht verschachtelten Brüche willst du aufreihen wie Perlen an einer Kette?

Cantor: Nun denn, betrachte zunächst einmal das Bild auf diesem Fetzchen Papier. Was zeigt es?

2

Sokrates: Es zeigt verschiedene Brüche. In der ersten Reihe sehe ich alle Brüche mit Zähler 1, in der zweiten Reihe mit Zähler 2 und so fort. In der ersten Spalte sind die Nenner 1, in der zweiten Spalte 2 und so weiter. Wenn ich es mir überlege, entstehen so alle Brüche, die man sich überhaupt vorstellen kann, wenn man sich diesen Teppich nach rechts und nach unten weitergeführt denkt.
Ich kann mir irgendeinen Bruch ausdenken, zum Beispiel 38/247. Ich finde ihn auf dem Teppich in der 38. Zeile und der 247. Spalte.
Nun, das erstaunt mich doch sehr: Auf der Zahlengeraden stellen die Brüche ein unübersichtliches Gewirr dar. Und hier liegen sie schön ausgebreitet auf einem Teppich! Dass dies möglich ist, finde ich bereits erstaunlich!

Cantor: Was denkst du nun, Sokrates, kannst du durch diesen Teppich von Brüchen einen Faden weben, der bei jedem Bruch einmal vorbeikommt? Kannst du also diese Brüche auf einen Faden aufreihen wie Perlen auf eine Kette?

Sokrates: Lass mich überlegen. Wenn ich mit dem Faden in der obersten Reihe beginne und ihn nach rechts führe, ... Nein, dann geht er unendlich lange nach rechts und ich gelange nicht zu den weiteren Reihen. Dasselbe passiert, wenn ich den Faden in der ersten Spalte nach unten ziehe.

Cantor: Kannst du den Faden anders ziehen, also nicht einfach waagrecht oder senkrecht?

Sokrates (studiert lange; plötzlich): Heureka! Ich hab's gefunden! Ich ziehe den Faden so durch:

3

Mit dieser Schlangenlinie erreiche ich alle Brüche! Keiner geht vergessen! Irgendwann kommt jeder auf den Faden! Und die Brüche, die Erweiterungen früher aufgezählter Brüche sind, überspringe ich einfach!

Cantor: Gut überlegt, Sokrates! Du siehst, man kann auf diese Weise die Brüche in eine Reihenfolge bringen, zwar nicht der Grösse nach, aber doch so, dass jeder Bruch aufgefädelt wird. Das sähe so aus: 1/1, 1/2, 2/1, 3/1, 1/3, 1/4, 2/3, 3/2, 4/1, 5/1, usw.
Jeder Bruch wird so erreicht, keiner geht vergessen.

Sokrates: Das verblüfft mich in der Tat. Ich hätte nie gedacht, dass man dieses Gewirr von Brüchen aufreihen kann. Nun stellt sich meine zweite Frage an dich aber noch dringender.

Cantor: Was ist diese zweite Frage?

Sokrates: Die Brüche kann man, ohne einen zu vergessen, aufreihen. Das hast du mir eben trefflich gezeigt. Aber nun behauptest du ferner, dass man eine solche Aufreihung für Dezimalzahlen nicht finden kann. Kannst du mich auch hierüber belehren und erleuchten?

Cantor: Bei deinen Geistesgaben wird dies ein Leichtes sein. Wir können uns sogar auf die Dezimalzahlen beschränken, die mit "Null-Komma..." beginnen. Sogar die lassen sich nämlich, wie ich dir gleich zeigen werde, nicht vollständig in einer Aufzählung anordnen.

Sokrates: Ich bin gespannt.

Cantor: Wir wollen jede Null-Komma-Zahl mit unendlich vielen Ziffern schreiben. Wenn eine Zahl also abbricht, setzen wir hinten noch unendlich viele Nullen an. Es gibt aber, wie du ja selber weisst, auch Dezimalzahlen, die nie abbrechen. Du selber hast ja einen von Menons Sklaven hierüber belehrt.
Nimm nun an, ein Zahlengenie, das viel klüger sei als wir beide habe durch einen genialen Einfall, der noch viel trickreicher sei als der Einfall mit dem Bruchzahlen-Teppich und deiner Schlangenlinie, eine Aufreihung der Null-Komma-Zahlen gefunden. Er schreibt diese Zahlenreihe untereinander. Kannst du dir das vorstellen?

Sokrates: Ich denke schon. Aber dieser kluge Mensch müsste ja klüger als Pallas Athene selber sein! Eine Anordnung zu finden, in der alle Null-Komma-Zahlen vorkommen... Aber wer weiss, vielleicht gibt es einen solchen genialen Weg, ähnlich wie das Schlangenlinien-Verfahren bei den Brüchen.
Das sähe dann etwa so aus (er zeichnet):

4

1.Zahl: 0.* * * * * * * ...(usw.)
2.Zahl: 0.* * * * * * * ...
3.Zahl: 0.* * * * * * * ...
4.Zahl: 0.* * * * * * * ...
5.Zahl: 0.* * * * * * * ...
6.Zahl: 0.* * * * * * * ...
7.Zahl: 0.* * * * * * * ...
...     ...................
(ins Unendliche weiter)

Die Sternchen bedeuten die einzelnen Ziffern jeder Dezimalzahl. Jede Zeile stellt eine solche Dezimalzahl dar: erste Zahl, zweite Zahl, und so weiter.

Cantor: Richtig. Betrachte nun die Ziffern, die in der Diagonale dieser Anordnung liegen. Färbe diese Ziffern wie folgt ein: Wenn die Ziffer ungerade ist, färbe sie rot, wenn sie gerade ist, färbe sie blau. Das könnte dann zum Beispiel so aussehen:

1.Zahl: 0.* * * * * * * ... (usw.)
2.Zahl: 0.* * * * * * * ...
3.Zahl: 0.* * * * * * * ...
4.Zahl: 0.* * * * * * * ...
5.Zahl: 0.* * * * * * * ...
6.Zahl: 0.* * * * * * * ...
7.Zahl: 0.* * * * * * * ...
...     ...................

Sokrates: Gut. Rot bedeutet also eine ungerade und blau eine gerade Ziffer. Worauf willst du nun hinaus?

Cantor: Ich will dir eine Zahl zeigen, die unser Genie vergessen hat, die in seiner Aufzählung nicht vorkommt, die nicht aufgefädelt wurde.

Sokrates: Wie soll das gehen?

5

Cantor: Betrachte die Zahl, die aus den farbigen Diagonalziffern besteht. Sie sieht in unserem Beispiel so aus:

0.* * * * * * * ...

Verändere nun diese Zahl, indem du überall die geraden Ziffern durch ungerade ersetzt und ungerade durch gerade. Du hast unzählige, genauer gesagt unendlich viele, Möglichkeiten dies zu tun. Wichtig ist nur der Farbwechsel der Ziffern, denn die neue Zahl färbt sich nun um und sieht so aus:

0.* * * * * * * ...

Sokrates: Gut, und du behauptest nun, dass diese Zahl in keiner bisherigen Reihe stehen kann?

Cantor: Genau das behaupte ich. Aber du kannst es selber einsehen.

Kann die Zahl

0.* * * * * * * ...

mit diesen Farben in der ersten Zeile stehen?

1.Zahl: 0.* * * * * * * ...
2.Zahl: 0.* * * * * * * ...
3.Zahl: 0.* * * * * * * ...
4.Zahl: 0.* * * * * * * ...
5.Zahl: 0.* * * * * * * ...
6.Zahl: 0.* * * * * * * ...
7.Zahl: 0.* * * * * * * ...
...     ...................

6

Sokrates (überlegt): Offensichtlich nicht, denn die erste Ziffer nach der Null hat die falsche Farbe.

Cantor: Gut bemerkt. Kann sie in der zweiten Reihe stehen?

Sokrates: Beim Zeus, nein, die zweite Ziffer ist rot statt blau! Und nun sehe ich, wie es weitergeht! Die dritte Zeile fällt auch weg, denn die dritte Stelle der Zahl ist rot statt blau. Bei der 4.Zeile passt die vierte Ziffer nicht, und so weiter. Die Zahl findet nirgends ihren Platz!

Cantor: Und wie stünde es in der 8. und 9. und allen folgenden Zeilen?

Sokrates: Da findet sie auch keinen Platz. Denn wir hätten ja unsere Zeichnung auch 8, 9, 10 Stellen und Zeilen lang machen können. Die umgefärbte Zahl kommt also in der ganzen unendlich langen Liste gar nicht vor!

Cantor: Hat das Genie eine falsche Anordnung gewählt? Wie, wenn es eine andere Anordnung wählte, die nun die vorhin entwischten Zahlen mit enthielte?

Sokrates: Dann kann ich die Ziffern wieder rot und blau einfärben und es gehen einfach andere Zahlen vergessen. Nie erwische ich alle! Beim Zeus, stets entgleiten beim Auffädeln einige (Was sage ich? Unendlich viele!) Zahlen! Es ist, als wolle man eine Herde Schafe in eine Reihe zwingen und stets springen einige davon! Die Brüche hingegen kann ich aufreihen; die sind im Gegensatz zu diesen Dezimalzahlen brav wie Kühe! Nun, immerhin war unser Genie also doch nicht klüger als Pallas Athene! Aber dir danke ich für deine Belehrung.

Ist die reelle Zahlengerade eine Linie?

Die Antwort aus neuerer Sicht muss "nein" lauten. Die Menge der reellen Zahlen wird aus historischen Gründen "Kontinuum" genannt. Man glaubte, die Lücken, welche die rationalen Zahlen offenliessen durch die Einführung der irrationalen Zahlen "zu füllen" und so die Zahlengerade zu etwas Kontinuierlichem zu machen (so wie man Schlaglöcher in einer Strasse auffüllt).

Neuere Überlegungen zeigen aber, dass man weitere Zahlen erfinden kann, z.B. die sogenannten Infinitesimalzahlen, die in der Non-Standard-Analysis benötigt werden. Man kann dann zeigen, dass jede Zahl auf der so erweiterten Zahlgeraden von einer "Hülle" von Infinitesimalzahlen umgeben ist und dass die Hüllen von noch so nahe beisammenliegenden Zahlen sich nie überlappen. In dieser Erweiterung rückt somit das Bild von etwas Kontinuierlichem in weite Ferne, vielmehr erscheinen hier die reellen Zahlen eher als isolierte Punkte.

Wir müssen somit feststellen: Die Zahlgerade ist keine Gerade im geometrisch-naiven Sinn. Die Zahlgerade besitzt keinen geometrischen Linien-Träger! Sie besteht einzig und allein aus den Zahlpunkten, die man betrachtet und aus nichts anderem! Von kontinuierlicher Linie kann keine Rede sein.

Was wir beim Zeichnen einer Zahlgeraden zeichnen (nämlich eine Lineal-Linie) hat so wenig mit der Zahlgeraden zu tun wie Bleistifthilfslinien in einem schön gestalteten Brief mit dem Inhalt des Briefes. Beides dient nur der schönen Ausrichtung. Wesentlich sind die (gedachten) Zahl"punkte". Dasselbe gilt für Funktionsgraphen: Auch sie bestehen eigentlich nicht aus einer Linie, sondern lediglich aus den reellen Zahl"punkten". Das ist auch der Grund, weshalb ein naiver geometrischer Begriff von "Stetigkeit einer Funktion" nicht möglich ist.

Eine Zahlgerade ist also keinesfalls eine mit Zahlen beschriftete geometrische Gerade! Trotzdem sollte man die Kontinuums-Idee nicht vorschnell verdammen: Die reellen Zahlen füllen ja tatsächlich Lücken, welche die Bruchzahlen offen lassen.

Wir können den roten Faden auch so durchführen, dass der "Einstieg" in den Teppich immer oben beginnt. Die Reihenfolge der Brüche sieht dann so aus:

1/1 - 1/2 - 2/1 - 1/3 - 2/2 - 3/1 - 1/4 - 2/3 - 3/2 - 4/1 - 1/5 - 2/4 - 3/3 - 4/2 - 5/1 - ...

Diesmal wollen wir die erweiterten Brüche früherer Brüche nicht streichen.

Der rote Faden geht wiederum durch alle Brüche hindurch, d.h. erreicht irgendwann einmal jeden Bruch, den es überhaupt gibt.

Denksport-Aufgabe:

Die Frage lautet nun: Können wir eine Formel finden, welche jedem Bruch a/b seine "Platznummer" auf diesem Faden zuordnet?

Eine solche Funktion p ordnet also jedem Paar (a, b) eine natürliche Zahl n zu, nämlich die Platznummer auf dem roten Faden: p (a, b) = n.

Wie lautet die Funktion p? Mit der links vorgeschlagenen Fadenführung lässt sich eine solche Funktion p in relativ einfacher Form finden.

Tipp: Die Brüche in der gleichen Fadendiagonalen haben jeweils die gleiche Zähler-Nenner-Summe: a + b = konstant auf einer Diagonalen.

(Lösung nachfolgend, linke Spalte)

Lösung obiger Denksportaufgabe:

Für alle Brüche mit a, b ≥ 1 gilt folgende Positionsformel p:

Beispiel: p (2, 4) = 5*4/2 + 2 = 12, d.h. der Bruch 2/4 hat Rang 12 auf dem Faden.

Aufgaben zu dieser Formel:

Welchen Rang auf dem roten Faden nimmt der Bruch 577 / 408 ein (es ist einer der ganz oben erzeugten Näherungsbrüche für √2 )?

Bereits schwieriger: Welcher Bruch steht auf Rang 100? Wie geht man hier am besten vor?

Vertiefende Aufgaben zur Aufzählung von Objekten:

1. Wie lautet eine mögliche Funktion, welche folgende Paare natürlicher Zahlen auf einen Faden reiht und die Rangnummer angibt? Aus Gründen der Erweiterungsfähigkeit soll die Aufzählung diesmal nicht bei 1, sondern bei 0 beginnen: 0, 1, 2, 3, ...

(0,0)  (0,1)  (0,2)  (0,3)  ...

(1,0)  (1,1)  (1,2)  (1,3)  ...

(2,0)  (2,1)  (2,2)  (2,3)  ...

(3,0)  (3,1)  (3,2)  (3,3)  ...

2. Ist die Menge der Zahlentripel (a,b,c) gebildet aus natürlichen Zahlen abzählbar (d.h. auf einen Faden aufreihbar)? Wie könnte das gehen?

3. Aus 2 folgt: Die Menge aller n-Tupel natürlicher Zahlen

(a1, a2, ..., an)

ist abzählbar.

Lösung zu 1:

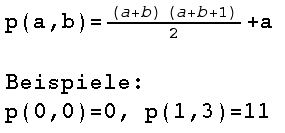
Lösung zu 2:

Wir ordnen die Tripel (a, b, c) so, dass wir mit der Ordnungsfunktion p zuerst das Paar (a, b) ordnen und dann durch erneute Anwendung von p das Paar (p(a, b), c). Die Ordnungsfunktion für Tripel baut sich dann so auf:

Aufgabe: Welches Tripel erhält die Ordnungsnummer 5? Welches die Ordnungsnummer 6? Man überzeuge sich, dass es zu jeder gegebenen Ordnungsnummer genau ein passendes Tripel gibt.

Eine Zahl heisst algebraisch, wenn sie die Nullstelle einer Polynomfunktion mit rationalen Koeffizienten ist. Da wir eine Gleichung f(x) = 0 mit rationalen Koeffizienten stets zu einer Gleichung g(x) = 0 mit ganzzahligen Koeffizienten erweitern können, sind alle algebraischen Zahlen auch Nullstellen von Polynomen mit ganzzahligen Koeffizienten.

Beispiele für algebraische Zahlen sind z.B. √2 (Lösung von x ²- 2 = 0) oder (√5 - 1)/2 und viele andere.

Eine Zahl, die nie als Lösung einer solchen Gleichung auftritt, heisst transzendent. Die Frage stellte sich: Gibt es überhaupt transzendente Zahlen oder sind alle reellen Zahlen algebraisch, d.h. Lösungen von Gleichungen g(x) = 0 mit rationalen Koeffizienten?

Man kann relativ einfach zeigen, dass es neben den algebraischen Zahlen auch transzendente Zahlen geben muss:

Man zeigt, durch Überlegungen wie oben, dass die Menge der Gleichungen g(x) = 0 mit ganzzahligen Koeffizienten abzählbar ist. Daraus folgert man, dass die Menge der algebraischen Zahlen ebenfalls abzählbar ist.

Da die Menge aller reellen Zahlen aber überabzählbar ist (nicht auf einen Faden aufreihbar, wie der Dialog oben zeigt), muss es neben den algebraischen Zahlen noch andere reelle Zahlen geben, eben die transzendenten Zahlen.

Dieser Gedankengang beweist zwar die Existenz transzendenter Zahlen, ohne jedoch konkrete Beispiele zu liefern. (Ein etwas "seltsames" Resultat: Man beweist, dass es bestimmte Dinge geben muss, ohne diese Dinge aber konkret angeben zu können.)

Ein konkretes Beispiel ist die Kreiszahl π. Dass π eine solche transzendente Zahl ist, d.h. dass π nie als Lösung einer Polynomgleichung g(x) = 0 mit rationalen Koeffizienten auftreten kann, ist nicht leicht zu beweisen und wurde erst 1882 gezeigt.

Ist jede Teilmenge reller Zahlen messbar?

Einige -allerdings nicht einfach zu verstehende- Überlegungen hier.