Der Begriff einer "Geraden" basiert zunächst auf ganz konkreten Dingen unserer physikalischen Umgebung: Seile, Fäden, Visierlinien, Grenzlinien, usw., d.h. auf der ganzen Palette von Erfahrungen, die wir in unserem kulturellen "Linien-Rundgang" beschreiben.
Eine Abstraktion von der Dicke oder der atomaren Feinstruktur solcher Gebilde ist nötig, um den Begriff der "Geraden" zu gewinnen.
Wir schauen also gewissermassen "nicht so genau hin", d.h. übersehen kleine Unregelmässigkeiten, übersehen die Dicke, usw. Das ist eine erste Abstraktionsstufe.
(Die Fähigkeit, "grosszügig" hinzuschauen, ist fürs abstrakte Denken sehr wichtig!*)
In einer nächsten Stufe werden nun verschiedene Geraden (und weitere elementargeometrische Elemente wie Punkte, Ebenen, Winkel, usw.) zueinander in Beziehung gesetzt.
Solche Beziehungen hat bereits Euklid in einem Axiomensystem formuliert. Die Mathematiker Hilbert und Pasch haben dieses Axiomensystem der euklidischen Geometrie noch perfektioniert.
Dabei kam es zu einer neuen Interpretation der Begriffe "Gerade", "Punkt", "Ebene": Die Axiome werden einfach als Grundspielregeln gesetzt; man fragt nicht mehr nach ihrer "Wahrheit". Das ganze Axiomensystem definiert indirekt (implizit), was Geraden, Punkte und Ebenen sind - einfach durch ihre Beziehungen zueinander.
Zu den Grundbeziehungen (Bsp: Geraden schneiden sich in Punkten; Punkte liegen auf einer Geraden oder nicht; Geraden gehen durch bestimmte Punkte oder nicht) kommen noch logische Schlüsse (Bsp: Alle Geraden haben eine Eigenschaft E. g ist eine Gerade. Also hat g die Eigenschaft E).
Das ganze System zusammen ergibt dann die euklidische Geometrie.
Ein formales System besteht also aus den axiomatisch festgelegten Grundbeziehungen zwischen den betrachteten Elementen und aus dem Apparat der logischen Schlussregeln.
Beim formalen Arbeiten mit dem euklidischen Axiomensystem kann man sich -wenn man will- immer noch die Alltagsbilder von "Geraden unserer physischen Welt" vorstellen. Solche Vorstellungen werden etwa auch in der Volksschuldidaktik aufgebaut und gepflegt (man kann z.B. einige Gesetzmässigkeiten zwischen Geraden und Punkten durch lange, dünne Papierstreifen veranschaulichen). Auch ist jede Skizze eine "physische Veranschaulichung". Die Gesetze der Geometrie folgen jedoch rein formal aus dem Axiomensystem.
Trotzdem: Das Axiomensystem ist mit Hilfe von Vorstellungen aus unserer physischen Welt entstanden und evoziert auch wieder solche Vorstellungen.
Nun ist eine weitere Abstraktionsstufe möglich: Man löst sich von den Alltags-Intuitionen der Grundgebilde, d.h. z.B. von der Alltags-Intuition einer Geraden und legt den Fokus aufs formale Operieren mit den Axiomen und den logischen Schlussregeln.
Zu den Axiomen der euklidischen Geometrie gibt es auch "Spiele" (oder Modelle), die sich von den üblichen Vorstellungen lösen und trotzdem in allen Teilen dem formalen System gehorchen.
Beispiel: Siehe Spalte rechts.
Siehe auch: Hilberts Axiomensystem der euklidischen Geometrie
-----
*) Dies gilt fürs Denken überhaupt und auch für jede Kommunikation: Wir wissen ungefähr, was die andere Person meint, wenn sie bestimmte Begriffe braucht. Würden wir jeden Begriff analysieren und hinterfragen, könnten wir gar nicht mehr kommunizieren. Die Begriffe haben im normalen Gebrauch (in einem "mittleren Bereich") eine einigermassen plausible Bedeutung. In Extrembereichen (Philosophie, Quantenphysik) werden die Bedeutungen dann problematisch.
Ein Beispiel (nach F.Gonseth: Le problème de la connaissance en philosophie ouverte, Verlag L'Age d'homme, Lausanne 1990, Hg. Eric Eméry, p.56):
Man wähle in der Ebene einen Punkt F als generellen Fixpunkt. Jeder Kreis, der durch F läuft, werde Gerade genannt. Der Winkel zwischen zwei solchen sogenannten Geraden sei der Winkel zwischen den beiden Kreisen. Man wechselt so die Namen und erhält ein System, das genau den Regeln der euklidischen Geometrie gehorcht, d.h. man erhält ein anderes Modell der euklidischen Geometrie (die Geraden sind hier die Kreise durch F).
Die Grund-Intuition einer "Geraden" (wie wir sie aus unserem Alltag haben) ist hier gekappt. Trotzdem funktioniert die Geometrie genau gleich wie die normale euklidische Geometrie.
Was jedoch noch nicht gekappt wurde, sind die Grund-Intuitionen der logischen Schlüsse, denn auch die formale Logik verdankt ihre Entstehung einigen Grund-Intuitionen, die wir seit frühestem Kindesalter erleben (ein Beispiel: Das Kind trägt die Katze, welche eine Gummimaus im Maul trägt; dann trägt das Kind auch die Gummimaus).
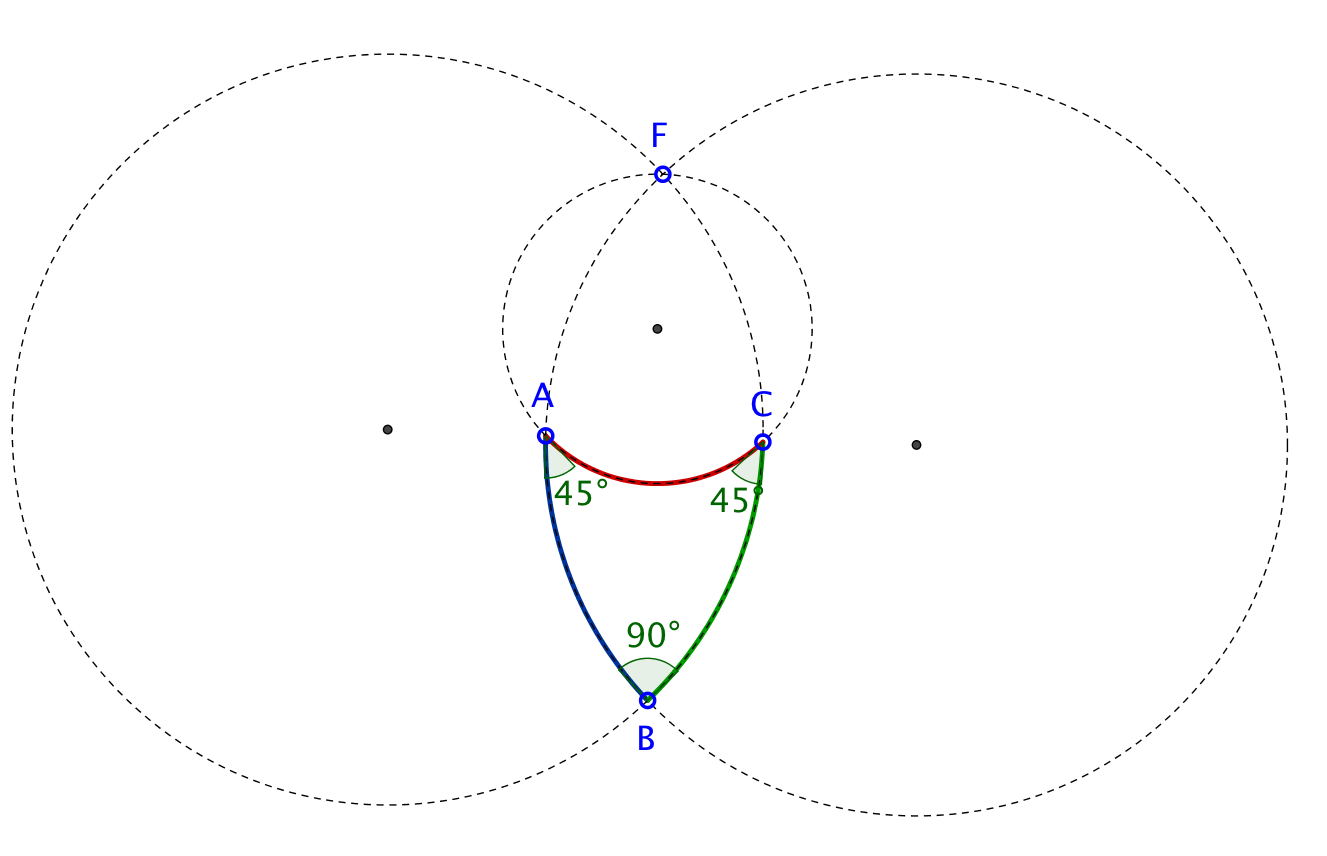
Ein gleichschenklig-rechtwinkliges Dreieck ABC im Gonseth-Modell der euklidischen Geometrie. Die Geraden sind Kreise durch F. Man erkennt, dass entsprechend den euklidischen Axiomen, denen das Modell genügt, die Winkelsumme 180° beträgt.
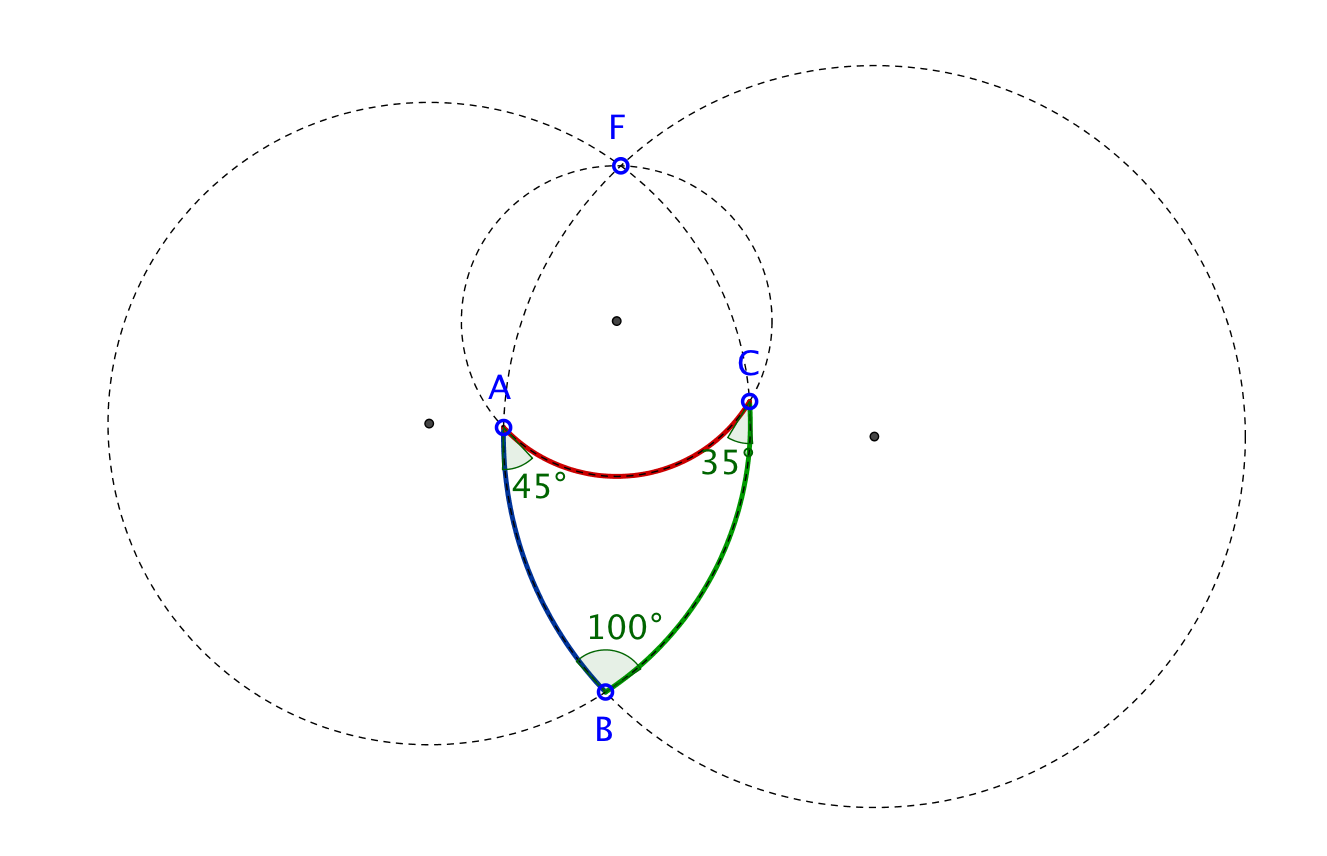
Ein anderes Dreieck. Winkelsumme wiederum 180°.
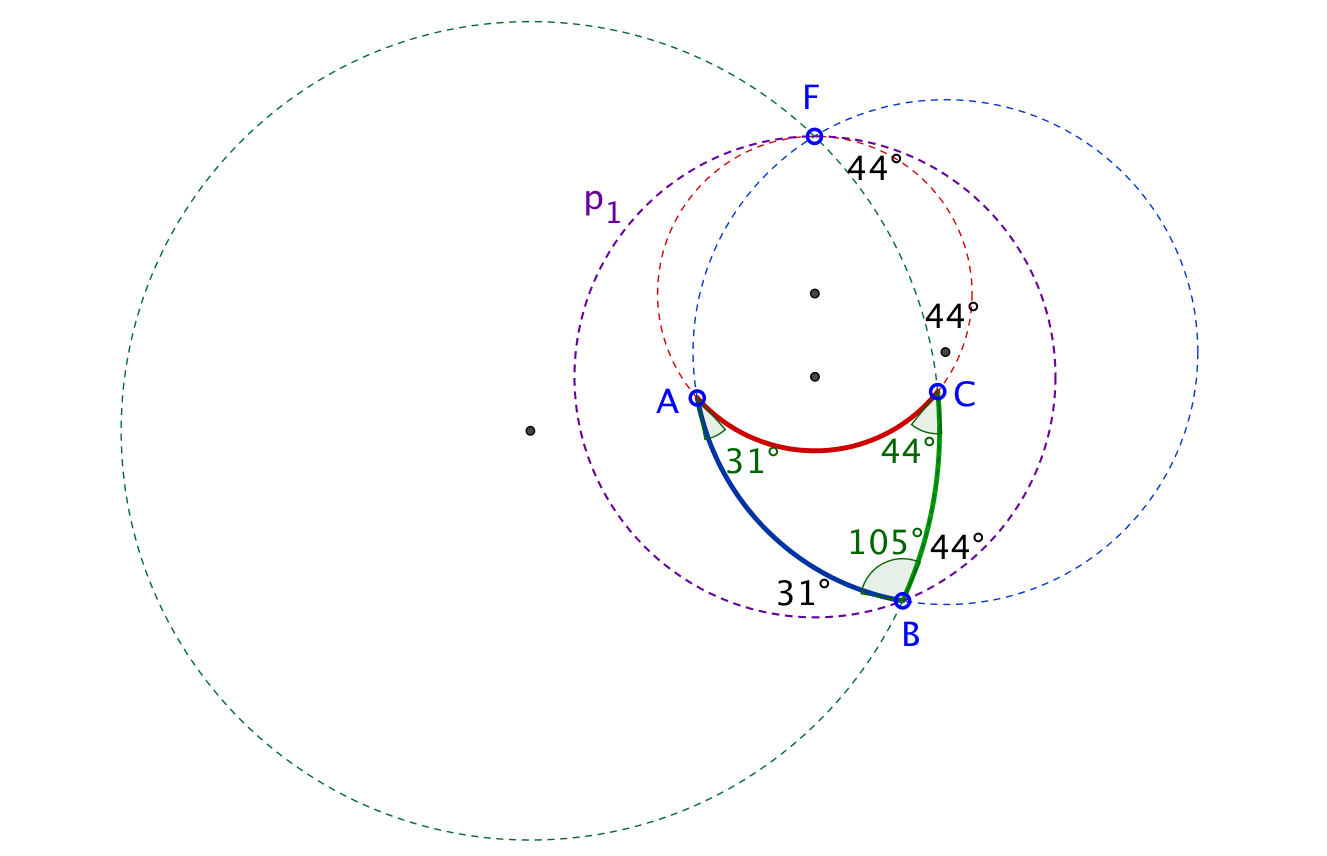
Der violette Kreis p1 stellt die eindeutig bestimmte "Parallele" zu AC durch den Punkt B dar: Kein Schnittpunkt (ausser F, der nicht zählt). Man sieht, dass entsprechend den euklidischen Gesetzen Wechselwinkel gleich gross sind. Bei B ergänzen sich die drei Winkel zu 180°. Da p1 eindeutig bestimmt ist, gilt das euklidische Parallelenaxiom: Zu einer Geraden AC gibt es durch einen ausserhalb von AC liegenden Punkt B genau eine Parallele.
Nun hat sich immer wieder die Frage gestellt, ob etwa das euklidische Parallelenaxiom, das postuliert, dass es zu einer gegebenen Geraden g durch einen Punkt ausserhalb von g genau eine Parallele gibt, ein Axiom sei oder ob dies aus den andern Axiomen hergeleitet werden könne. Dabei hat man Geometrien entdeckt, welche alle Axiome der euklidischen Geometrie erfüllen - mit Ausnahme des Parallelenaxioms.
Somit ist klar, dass es Geometrien gibt, die ohne das Parallelenaxiom auskommen; dieses ist somit wirklich ein Axiom der euklidischen Geometrie, d.h. nicht herleitbar aus den andern Axiomen (sonst könnte es ja die neu entdeckten nicht-euklidischen Geometrien gar nicht geben).
Nach der Entdeckung der nicht-euklidischen Geometrien hat man viele weitere Geometrien entdeckt. Die Grundbegriffe (z.B. der Begriff der "Geraden") sind dabei neu interpretiert und decken sich nicht mehr mit unserem Alltagsbegriff einer Geraden.
Im folgenden ist eine 9-Punkte-Geometrie aufgeführt, die mit 3 Axiomen formalisiert ist (eines davon ist das Parallelenaxiom):
Eine Geometrie mit 9 Punkten

Bild einer 9-Punkte-Geometrie
Wir lösen uns vom anschaulichen Begriff einer Geraden. Eine "Gerade" soll einfach eine Verbindung zweier Punkte sein. Die 12 farbigen Gebilde links (3 rote, 3 blaue, 3 grüne, 3 gelbe) seien also die "Geraden" dieser 9-Punkte-Geometrie.
Es gelten folgende Axiome:
A1. Zu je zwei Punkten gibt es genau eine Verbindungsgerade. [Beispiel: A und F sind durch eine gebogene rote Linie verbunden.]
A2. Zu jeder Geraden und jedem Punkt ausserhalb dieser Geraden gibt es genau eine Gerade, die mit der gegebenen Geraden keinen Punkt gemeinsam hat, d.h. genau eine "Parallele" (Parallelenaxiom).
A3. Es gibt drei Punkte, die nicht auf einer Geraden liegen, d.h. es gibt mindestens ein Dreieck. [Beispiele von Dreiecken: ABE, ABF]
Eine Struktur, welche obige Axiome 1- 3 erfüllt, heisst "affine Ebene".
Die endliche Geometrie im Bild oben hat 9 Punkte und 12 Verbindungslinien, die wir "Geraden" nennen. Jede Gerade besitzt 3 Punkte. Die Geraden sind also die farbigen Verbindungslinien zwischen zwei Punkten. Wir nennen also auch die gebogenen Verbindungen Geraden (z.B. FG).
Durch jeden Punkt gehen vier Geraden (von jeder Farbe eine).
Wie in der "gewöhnlichen", euklidschen Geometrie definieren wir, wann zwei Geraden parallel genannt werden sollen: Zwei Geraden heissen parallel, wenn sie entweder identisch sind oder wenn sie keinen Punkt gemeinsam haben. Welche Geraden im Bild oben sind demnach parallel?
[Lösung: Genau die gleichfarbigen Geraden sind je unter sich parallel.]
Frage: Welche Geraden dieser Geometrie könnten "senkrecht zueinander" genannt werden?
Einführung von Koordinaten auf dieser Geometrie:
Wir führen ein Koordinatensystem ein, indem wir dem Punkt A die Koordinaten (0 | 0), dem Punkt B (1 |0) und dem Punkt D (0 | 1) zuordnen. Weil die Geometrie endlich ist, man aber beliebig oft eine Koordinateneinheit addieren kann, muss der Zahlbereich, aus dem die Koordinaten stammen endlich sein. Man wählt als Koordinaten die sogenannten Dreier-Restklassen. Das sind die Reste, die eine Zahl bei Division durch 3 bildet. Da gibt es nur 3 Möglichkeiten: Rest 0, Rest 1 oder Rest 2.
Zahl: 0 1 2 3 4 5 6...
3er-Rest: 0 1 2 0 1 2 0...
Wir rechnen nur mit den Resten 0, 1 und 2. Es gilt z.B.: Eine Zahl mit Rest 2 plus eine Zahl mit Rest 1 ergibt eine Zahl mit Rest 0. Dies schreiben wir so:
2 + 1 = 0. Analog folgt z.B. 2 + 2 = 1.
Wir können diese Dreierrestzahlen auch miteinander multiplizieren: Es gilt z.B.
2 * 2 = 1.
Hier die Operationen + und * in einer Additions- und einer Multiplikationstabelle:
+ 0 1 2 * 0 1 2
0 0 1 2 0 0 0 0
1 1 2 0 1 0 1 2
2 2 0 1 2 0 2 1
Da 2 + 2 = 1 ist, folgt: 2 ist die Hälfte von 1 oder 2 = 1/2.
Fortsetzung: Koordinaten in der 9-Punkte-Geometrie:
Die Punkte haben folgende Koordinaten:
A(0 | 0), B(1 | 0), C(2 | 0), D(0 | 1), E(1 | 1), F(2 | 1), G(0 | 2), H(1 | 2), I(2 | 2)
Mittelpunkt zweier Punkte: Die Koordinaten des Mittelpunkts zweier Punkte sind der Durchschnitt der Koordinaten der Punkte. Beispiel:
Mittelpunkt der Strecke AC: ((0 + 2)/2 | (0 + 0)/2) = (1 | 0) = Punkt B.
Mittelpunkt der Strecke AB: ((0 + 1)/2 | ((0 + 0)/2) = (1/2 | 0) = (2 | 0) = C. In dieser seltsamen 9-Punkte-Geometrie ist der Mittelpunkt zweier Punkte stets der dritte Punkt auf der entsprechenden Geraden! Mit unserer gewöhnlichen "Intuition" von "Mitte" hat dies nichts mehr zu tun.
Geradengleichungen:
Beispiel: Gleichung der Geraden DC: Wir setzen: y = mx + q.
D eingesetzt: 1 = m*0 + q => q = 1
C eingesetzt: 0 = m*2 + 1 => 2m = -1 = 2 => m = 1
Die Gleichung der Geraden DC ist folglich y = x + 1.
Senkrechte:
Zwei Geraden sollen auch in dieser Geometrie senkrecht aufeinander stehen, wenn das Produkt ihrer Steigungen = -1 ist. -1 ist aber hier gleich 2. Zwei Geraden stehen somit senkrecht aufeinander, wenn ihre Steigungen das Produkt 2 haben. Zudem sollen die Geraden mit Steigung 0 senkrecht auf den Geraden mit Steigung unendlich sein.
Rote Geraden: Steigung -1 = 2.
Blaue Geraden: Steigung 1.
Grüne Geraden: Steigung 0.
Gelbe Geraden: Steigung unendlich.
Die roten und die blauen Geraden stehen senkrecht aufeinander, ebenso die grünen und die gelben.
Einige "seltsame" Resultate der 9-Punkte-Geometrie:
- Die 3 Seitenhalbierenden jedes Dreiecks sind zueinander parallel.
- Die Höhen jedes Dreiecks schneiden sich in einer Dreiecksecke.
- Jedes Dreieck ist gleichschenklig-rechtwinklig.