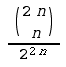Random Walks
Random Walks spielen z.B. in der Theorie der Diffusion von Teilchen oder bei der Analyse von Daten (Vergleich einer medikamentös behandelten Gruppe mit einer Blilndgruppe) eine Rolle. Francis Galton (1822 - 1911) beschrieb 1876 in einer Mitteilung an Charles Darwin ein solches Verfahren, um abzuschätzen, ob eine gewisse Behandlung wirkungsvoll sei oder nicht (Galton's rank-order test, Biometrika, vol 42, 1955, pp. 261-262; vgl. Weblink: http://biomet.oxfordjournals.org).
A und B spielen Münzwerfen. Abwechslungsweise wird geworfen. A gewinnt bei "Kopf", B bei "Zahl". Der Spielverlauf wird grafisch aufgezeichnet: Gewinnt A einen Wurf, wird eine Strecke mit Steigung 1 (schräg nach oben rechts) gezeichnet (Δx und Δy je 1). Gewinnt B, wird eine Strecke mit Steigung -1 gezeichnet (Δx = 1, Δy = -1).
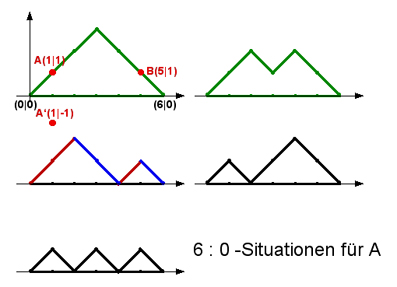
Die Abbildungen 1 und 2 zeigen mögliche Spielverläufe, bei denen A und B je 3-mal werfen (n = 3; das ergibt total 2n = 6 Münzwürfe).
Beispiel Abb. 1, drittes Teilbild in rot-blauer Färbung: Zuerst gewinnt A zweimal, dann B zweimal, dann A einmal, dann B einmal.
Wir betrachten vorläufig nur Situationen, bei denen am Schluss ein Unentschieden entsteht (A und B haben am Schluss gleich oft gewonnen).
Bei Spielen, die am Schluss unentschieden ausgehen, bei denen der Spielpfad also wieder auf der x-Achse endet, sind für 2n = 6 folgende Spielverläufe möglich:
- A liegt 6 Mal in Führung, B nie. (Wir sagen, dass A in Führung liegt, wenn die aktuell jüngste Verbindungsstrecke oberhalb der x-Achse liegt.)
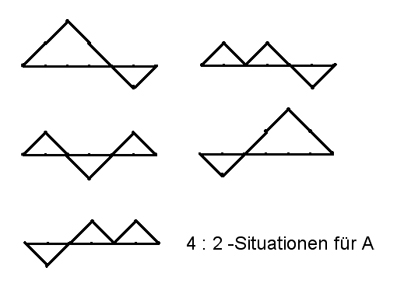
- A liegt 4 Mal in Führung, B 2 Mal.
- A liegt 2 Mal in Führung, B 4 Mal.
- A liegt nie in Führung, B 6 Mal.
Wir vermuten vielleicht bereits, dass zu jeder dieser 4 Möglichkeiten gleich viele (nämlich 5) verschiedene Pfade existieren. Dies wird zu beweisen sein.
Im Beispiel 2n = 6 (oder n = 3) gewinnen sowohl A wie auch B je drei Mal. Von den 6 Teilstrecken des Spielgraphen sind somit 3 Strecken steigend (im 3. Teilbild von Abb. 1 rot markiert), die übrigen 3 sind fallend (blau). Wir haben also 3 steigende ("rote") Strecken auf 6 mögliche Plätze zu verteilen. Das ergibt
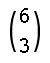
= 20 oder allgemein
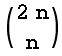
Möglichkeiten.
Wir finden somit:
Satz 1: Für n Würfe von A und n Würfe von B (total 2n Würfe) gibt es
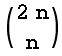
mögliche Spielverläufe, die unentschieden enden.
Die Abbildungen 1 und 2 zeigen 10 dieser Verläufe für n = 3 (oder 2n = 6) . Die übrigen 10 Verläufe entstehen durch Spiegelung an der x-Achse.
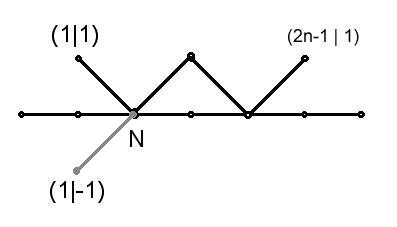
Abb. 3: n = 3 oder 2n = 6. Wege von (1 | 1) nach (5 | 1) mit x-Achsenkontakt.
Gemäss Herleitung rechts ergeben sich 4 solche Wege.
Pfade, welche die x-Achse weder berühren noch schneiden, seien im Folgenden Pfade "ohne x-Achsen-Kontakt" genannt, Pfade, welche die x-Achse irgendwo berühren oder schneiden, seien Pfade "mit x-Achsen-Kontakt" genannt.
Satz 2: Die Anzahl der Pfade von (1 | 1) nach (2n -1 | 1) mit x-Achsen-Kontakt ist gleich der Anzahl aller Pfade von (1 | -1) nach (2n-1 | 1).
Begründung: Sei N die erste Nullstelle des Pfades von (1 | 1) nach (2n-1 | 1). Jedem Pfad von (1 | 1) nach (2n-1 |1) mit x-Achsen-Kontakt entspricht eindeutig derjenige Pfad, dessen Anfangsstück von (1 | -1) bis N das Spiegelbild bezüglich der x-Achse des ursprünglichen Pfades ist (hellgrau gezeichnet) und dessen Schlussstück von N bis (2n-1 | 1) mit dem ursprünglichen Pfad übereinstimmt.
Wie gross ist diese Anzahl?
Wir bestimmen die Gesamtzahl der Wege von (1 | -1) nach (2n-1 | 1). Es sind 2n-2 steigende oder fallende Streckenabschnitte zu "vergeben". Dabei hat es 2 steigende Abschnitte mehr als fallende (Anstieg von y = -1 auf y = +1). Das ergibt n steigende und n-2 fallende Streckenabschnitte. Wir haben somit n steigende Abschnitte auf 2n-2 Plätze zu verteilen. Dies ist möglich auf
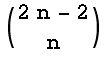
Arten. Dies ist auch die Anzahl der Pfade von (1 | 1) nach (2n-1 | 1) mit x-Achsen-Kontakt.
Satz 3: Die Anzahl der Pfade von (1 | 1) nach (2n-1 | 1) ohne x-Achsenkontakt ist gleich der Anzahl aller Pfade von (1 | 1) nach (2n-1 | 1) minus der Anzahl Pfade von (1 | 1) nach (2n-1 | 1) mit x-Achsenkontakt, somit gleich 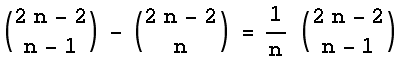 .
.
Die letzte Gleichheit ergibt sich leicht aus der Definition der Binomialkoeffizienten.
Daraus ergibt sich nun unmittelbar Satz 4.
Satz 4: Die Anzahl der Pfade von (0 | 0) nach (2n | 0), die oberhalb der x-Achse verlaufen und die mit Ausnahme der Randpunkte keinen x-Achsenkontakt haben, ist ebenfalls gleich
 .
.
Im Beispiel n = 3, 2n = 6 ergeben sich 2 Wege. Es sind die ersten beiden Wege (grün gezeichnet) von Abb. 1.
Dazu verschieben wir das Koordinatensystem in y-Richtung um 1 nach unten:
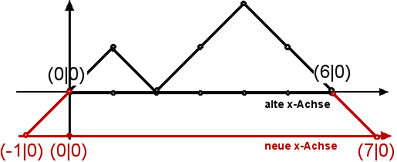
Dann sind die gesuchten Wege im neuen Koordinatensystem (rot) genau die Wege von (-1 | 0) nach (2n+1 | 0), welche ausser den Randpunkten keine weiteren Kontakte zur neuen, roten x-Achse mehr haben. Wir benützen also das Ergebnis von Satz 4, indem wir dort statt n den Wert (n + 1) einsetzen. Es ergibt sich folgende Anzahl:
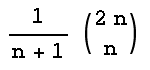 .
.Es folgt
Satz 5: Die Anzahl Wege von (0 | 0) nach (2n | 0), welche gänzlich oberhalb der x-Achse verlaufen und diese höchstens berühren (aber nie schneiden), ist gleich
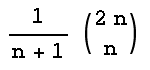 .
.
Im Beispiel mit n = 3 oder 2n = 6 ergibt obige Formel 20 : 4 = 5 Wege. Es sind die 5 Wege von Abb.1, welche alle oberhalb der x-Achse verlaufen und diese höchstens berühren, d.h. alle Wege, bei denen Person A stets führt (Führungsverhältnis 6 : 0).
Es bleibt noch zu zeigen, dass die durch obige Formel gegebene Anzahl Wege für alle Führungsverhältnisse dieselbe ist (Satz 6), dass es also gleich viele Wege mit Führungsverhältnis (6 : 0), (4 : 2), (2 : 4), (0 : 6) gibt. Die Gesamtzahl
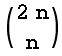
aller Wege wird damit gleichmässig auf die (n + 1) verschiedenen Führungsverhältnisse aufgeteilt. Der Beweis kann mittels vollständiger Induktion nach n geführt werden.
Diskussion von Satz 6 :
Dass alle möglichen Führungsverhältnisse gleich wahrscheinlich sind, hat zur Folge, dass häufige Führungswechsel nicht sehr wahrscheinlich sind. Im Beispiel n = 3 (bzw. 2n = 6) haben wir von den 20 möglichen Wegen, die in einem Unentschieden enden
- 10 Wege ohne jeden Führungswechsel (entweder ist immer A oder immer B in Führung; das Unentschieden entsteht erst ganz am Schluss)
- 8 Wege mit genau einem Führungswechsel und
- 2 Wege mit genau zwei Führungswechseln.
Für n = 3, 2n = 6 und unentschiedenem Schlussresultat bleibt also diejenige Person, die den ersten Münzwurf gewinnt mit 50% Wahrscheinlichkeit bis zum letzten Wurf in Führung; mit 40% Wahrscheinlichkeit wechselt die Führung einmal und mit nur 10% Wahrscheinlichkeit wechselt sie zweimal.
Galtons Anwendung auf einen Rangtest :
Es werde z.B. ein Wachstumspräparat für Pflanzen getestet. Messgrösse sei die Höhe der Pflanze, wenn sie ausgewachsen ist. Man behandelt n Pflanzen mit dem Präparat (Messresultate a1, a2, a3, ..., an); weitere n Pflanzen bilden die Blindgruppe (Messresultate b1, b2, b3, ..., bn). Die Messresultate jeder Gruppe werden nach absteigender Grösse geordnet: a1> a2> a3> ...> an und b1> b2> b3> ...> bn.
Nun kombinieren wir die beiden Sequenzen nach absteigender Grösse. Dies ergibt eine gemischte Sequenz von 2n Grössen. Bei einer sehr erfolgreichen Behandlung mit dem Wachstumspräparat sollten alle a-Elemente vor den b-Elementen stehen; bei einer ineffektiven Wirkung sollten die a- und die b-Elemente in der gemischten Kette zufällig verteilt sein.
Die Wahrscheinlichkeit, dass die a-Elemente genau 2k-mal führen (d.h. dass genau 2k Elemente ai grösser sind als das zugehörige bi mit gleichem Index i), ist nach Satz 6 gleich 1 / (n + 1). Die Wahrscheinlichkeit, dass die a-Elemente 2k-mal oder mehr in Führung liegen ist gleich (n - k + 1) / (n + 1).
In Galtons Beispiel war n = 15, d.h. er testete 15 a-Pflanzen und 15 b-Pflanzen (Blindgruppe). Die a-Pflanzen führten 26-mal, d.h. 2k = 26 oder k = 13. Für Galton war dies ein Zeichen der Wirksamkeit der getesteten Substanz. Die Wahrscheinlichkeit, dass die a-Elemente 26-mal oder öfter in Führung liegen, wenn dies zufällig zustande käme ist gleich (15-13+1) / (15+1) = 3/16 = 18.75%. Nach heutigen Massstäben ist diese Irrtumswahrscheinlichkeit (man hält die Wirksamkeits-Hypothese für richtig, obwohl das Resultat zufällig zustandegekommen ist) zu hoch, um die Wirksamkeit der getesteten Substanz positiv beurteilen zu können. Es wäre eine viel höhere Anzahl von Versuchspflanzen nötig gewesen.
Random Walks (Münzwürfe), die nicht auf der x-Achse enden müssen:
Die Münze werde 2n-mal geworfen. Wir können uns vorstellen, dass dies in einem konstanten Zeitrhythmus geschieht (Zeiteinheit 1 zwischen zwei Würfen). Wenn ein Unentschieden eintritt (Schnittpunkt mit x-Achse), so sagen wir, es habe eine Rückkehr zum Anfangszustand stattgefunden. Ein in y-Richtung diffundierendes Teilchen befindet sich dann z.B. wieder am Anfangsort y = 0, d.h. auf der x-Achse.
Es gibt 22n Wege der Länge 2n (startend bei (0 | 0)). Bei einer Laplace-Münze sind sie alle gleichwahrscheinlich.
Satz 7: Die Wahrscheinlichkeit, dass
a) zur Zeit 2n eine Rückkehr zum Anfangszustand stattfindet
b) bis und mit Zeitpunkt 2n keine Rückkehr zum Anfangszustand stattfindet
c) der Pfad zwischen 0 und 2n nicht-negativ verläuft
ist in allen drei Fällen gleich