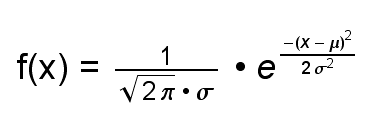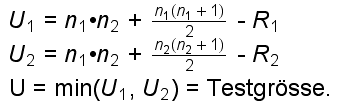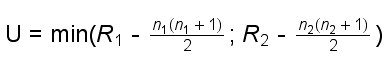13. Ist die Münze gerecht? - Signifikanztests

Bemerkung Im hervorragenden Buch "Teaching Statistics - a bag of tricks" von Andrew Gelman und Deborah Nolan, Oxford University Press, ISBN 0 19 857224 7, p. 114 ff, wird darauf hingewiesen, dass eine Münze immer gerecht ist, auch wenn sie einseitig gewichtet ist. Die "ungerechte Münze", die in vielen Beispielen -so auch hier- auftaucht, sei das "Einhorn der Statistik", also ein Mythos. Auch wenn die Schwerpunktsebene nicht mit der Mittelebene der Münze übereinstimmt, rotiert die aufgeworfene Münze in der Luft sehr schnell und regelmässig (einfach um eine Achse durch ihren Schwerpunkt). Das Fangen und das Ergebnis "Kopf" oder "Zahl" erfolgt dann immer so, dass Wahrscheinlichkeit 0.5 resultiert. Wie können wir unser Beispiel "retten"? Wir können uns z.B. jemanden vorstellen, der die Münze auf spezielle Art wirft (ohne grosse Rotationen in der Luft) und geübt ist, sie vermehrt auf "Kopf" landen zu lassen. Besser wäre es, zu einem Würfel zu greifen: Anstelle der Zahlen 1 - 6 trägt er auf 3 Flächen den Buchstaben K ("Kopf") und auf 3 Flächen den Buchstaben Z ("Zahl"). Einen Würfel kann man nun fälschen, indem man ihn ungleichmässig gewichtet. Der Einfachheit halber belassen wir es jedoch im Folgenden bei unserem statistischen Einhorn. |
Wir möchten testen, ob eine Münze "gerecht" sei, d.h. ob beim Münzwurf mit gleicher Wahrscheinlichkeit p = 0.5 "Kopf" oder "Zahl" erscheint. Wir werfen die Münze z.B. 50-mal. Sei die Zufallsvariable X die "Anzahl Köpfe" in diesen 50 Würfen. X kann somit die Werte 0 bis 50 annehmen. Wir sagen, X sei unsere Testgrösse.
Wann wollen wir die Münze als "gerecht" ansehen? Sicher wird auch eine gerechte Münze in 50 Würfen nicht einfach exakt 25-mal Kopf zeigen. Bei jeder Wiederholung dieses Experiments werden auch bei einer gerechten Münze Abweichungen vom Erwartungswert 25 auftreten. Welche Abweichungen wollen wir aber noch tolerieren? Im Extremfall sind auch bei einer gerechten Münze hohe Abweichungen vom Wert 25 möglich, allerdings haben solche Extremfälle eine kleine Auftretens-Wahrscheinlichkeit.
Wir entscheiden uns z.B., folgende Werte für X nicht mehr zu akzeptieren:
{0, 1, ..., 17, 33, 34, ..., 50}. Diesen Bereich nennen wir Verwerfungsbereich. Er ist von uns vorerst einmal willkürlich gewählt.
Wir haben nun folgende Situation:
- Hypothese H0: P("Kopf") = 0.5 = Nullhypothese.
- Hypothese H1: P("Kopf") ≠ 0.5 = Alternativhypothese.
- Testgrösse: X = Anzahl Kopf bei 50 Münzwürfen.
- Verwerfungsbereich für H0: V = {0, 1, ..., 17, 33, 34, ..., 50}. Falls X ∈ V, verwerfen wir H0.
Beim Testen von Hypothesen geht man stets davon aus, dass man die Nullhypothese widerlegen will. Die Nullhypothese wird mathematisch mittels eines Gleichheitszeichens formuliert: P("Kopf") = 0.5, während die Alternativhypothese offener ist: P("Kopf") ≠ 0.5.
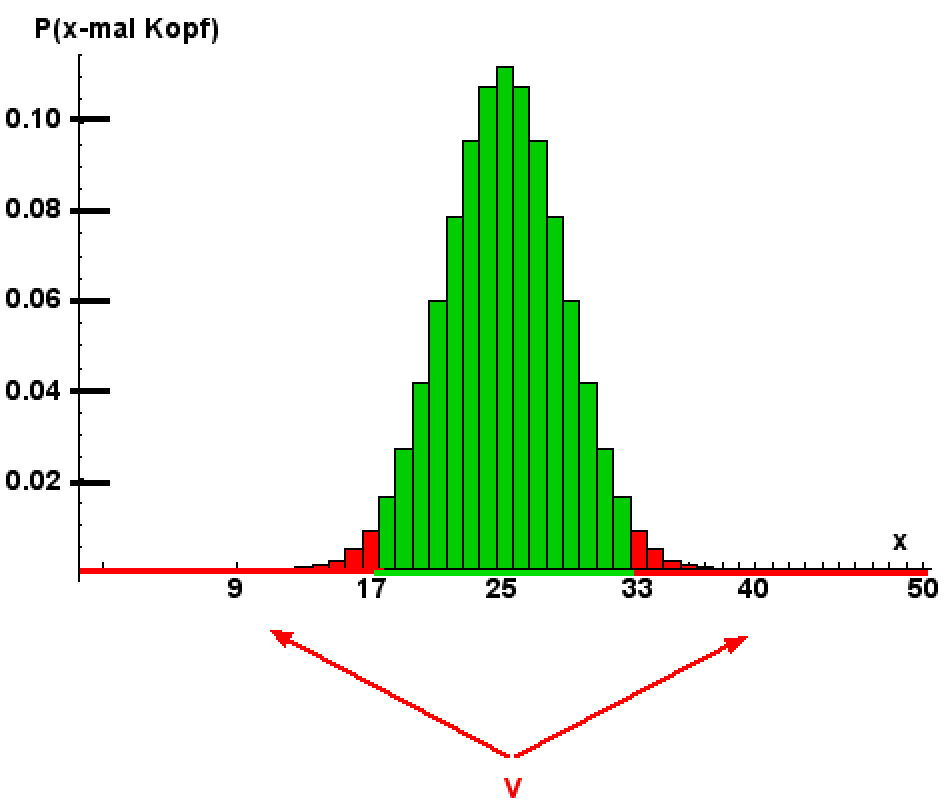
Binomialverteilung P("x-mal Kopf in 50 Münzwürfen"). Rot: Verwerfungsbereich V, grün: Annahmebereich. Die Gesamtfläche der Histogrammsäulen beträgt 1. Die Fläche der roten Säulen macht 3.28% der Gesamtfläche aus. Mit dieser Wahrscheinlichkeit landet eine gerechte Münze im "roten Bereich", d.h. wird H0 zu Unrecht verworfen. |
Es können beim Testen zwei Arten von Fehlern auftreten:
- Fehler 1. Art: H0 wird zu Unrecht verworfen: Es könnte ein "Extremfall" eingetreten sein, der einen Wert aus dem Verwerfungsbereich ergibt, obwohl H0 gilt.
Solche Fehler sind aus wissenschaftlicher Sicht schlecht. Will ein Forscher eine neue Hypothese H1 stützen (z.B. eine neue Therapie, die erfolgreicher sein will, als die alte), muss er H0 ablehnen können (H0 wäre: alte Therapie, also status quo, ist gleich wirksam wie neue). Ein Fehler 1. Art würde also H0 zu Unrecht ablehnen, d.h. die Hypothese stützen, die neue Therapie sei erfolgreicher als die alte, obwohl dies nicht stimmt. Solche Fehler -publiziert- können einen grossen Reputationsschaden anrichten.
- Fehler 2. Art: H0 wird zu Unrecht beibehalten. In Bezug auf das Therapiebeispiel oben ist man hier also "zu konservativ", zu vorsichtig: Man hält die alte Therapie für gleich wirksam wie die neue, obwohl die neue vermutlich besser wäre. Hier wird kein Reputationsschaden entstehen - der Forscher mit diesem Ergebnis wird die neue Therapie gar nicht als Novum anpreisen. Trotzdem ist natürlich auch ein solcher Fehler lästig: Er lässt Dinge übersehen, die zu wissen gut wäre.
Wir sind zunächst einmal bestrebt, die Wahrscheinlichkeit α für einen Fehler 1. Art möglichst klein zu halten. Dazu darf der Verwerfungsbereich nicht zu grosszügig bemessen sein, sonst verwerfen wir H0 zu unkritisch. In Bezug auf unsere Farben im Histogramm links bedeutet das: Sei sparsam mit der roten Farbe!
Wie sieht es in unserem Beispiel aus? Mit welcher Wahrscheinlichkeit erzeugt eine Münze, welche H0 genügt, also eine gerechte Münze, bei 50 Würfen einen Wert im Verwerfungsbereich?
Wir wissen: P("k-mal Kopf") = (50 tief k)* 0.5k * 0.550-k = (50 tief k)*0.550 .
Wir haben zu berechnen: P("0-mal Kopf") + P("1-mal Kopf) + ... + P("17-mal Kopf") + P("33-mal Kopf") + ... + P("50-mal Kopf") = 3.28% = α.
Mit dem gewählten Verwerfungsbereich V = {0, 1, ..., 17, 33, 34, ..., 50} ist somit die Wahrscheinlichkeit eines Fehlers 1. Art 3.28%, d.h. mit der Wahrscheinlichkeit 3.28% taxieren wir eine gerechte Münze fälschlicherweise als ungerecht, d.h. verwerfen H0 fälschlicherweise.
Unser Verwerfungsbereich hat von beiden Extrem-Enden des Spektrums her seine Elemente rekrutiert: von 0-mal Kopf bis 17-mal Kopf und von 50-mal Kopf retour bis 33-mal Kopf (unser Histogramm wurde von beiden Seiten her rot maniküriert). Deshalb nennt man einen solchen Test zweiseitig.
Falls also in unserem 50-Würfe-Versuch die Anzahl Köpfe in den Verwerfungsbereich fällt, sagen wir, dass wir die Hypothese H0 ("Münze gerecht") auf dem Signifikanzniveau 3.28% verwerfen.
Falls die Testgrösse "Anzahl Kopf" nicht in den Verwerfungsbereich fällt (sondern in den Annahmebereich {18, ... , 32}), behalten wir vorläufig die Hypothese H0 bei. Das muss nicht bedeuten, dass H0 tatsächlich richtig ist, sondern heisst nur, dass wir mit unserem Test H0 nicht widerlegen konnten.
Üblich sind Signifikanzniveaus von 5%, 2.5% oder -in medizinisch wichtigen Fällen- 1%. Niveaus über 5% gelten nicht mehr als signifikant. So würden wir beispielsweise mit einem Verwerfungsbereich von 0 bis 18 und von 32 bis 50 ein α von bereits 6.49% erhalten. Dieser Verwerfungsbereich würde somit kein signifikantes Ergebnis mehr liefern, er wäre zu gross gewählt.
Einseitiger Test
Herr Schlau hat eine spezielle Münze, die er für Wetten braucht. Er wettet jedes Mal auf "Kopf". Nachdem wir gegen ihn einigemale verloren haben, vermuten wir, dass seine Münze gefälscht ist, jedoch so, dass die Wahrscheinlichkeit für "Kopf" grösser ist als 0.5. Unsere Hypothesen sehen also in diesem Fall so aus:
- Hypothese H0: P("Kopf") = 0.5 = Nullhypothese ("Münze gerecht")
- Hypothese H1: P("Kopf") > 0.5 = Alternativhypothese.
- Testgrösse: X = Anzahl Kopf bei 50 Münzwürfen.
- Verwerfungsbereich: Wir wollen einmal V = {32, ..., 50} wählen.
Wir finden: Mit einer Wahrscheinlichkeit α von 3.24% lehnen wir H0 irrtümlich ab, d.h. bezichtigen wir Herrn Schlau irrtümlicherweise der Fälschung. D.h. eine wirklich gerechte Münze würde lediglich mit einer Wahrscheinlichkeit von 3.24% ein Extremresultat aus V = {32, ..., 50} ergeben; wahrscheinlicher ist da eher eine Fälschung. Nun haben wir V einseitig gewählt, d.h. einen einseitigen Test durchgeführt. Dies konnten wir aber nur deshalb tun, weil wir ein Vorwissen besassen (wir kannten Herrn Schlau und seinen Hang zum Schummeln) und aufgrund dieses Vorwissens vermuteten, dass die Münze einseitig gefälscht sei (in Richtung "mehr Kopf als normal"). Wenn solches Vorwissen nicht vorliegt oder zweifelhaft ist, teste man -im Zweifelsfalle- zweiseitig.
In unserem Beispiel ist μ = 25 und σ2 = 12.5. |
Ablesen der Verwerfungsgrenzen bei der Normalverteilung
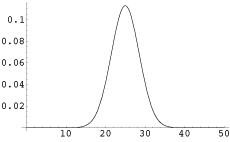

Links: Normalverteilung anstelle der Binomialverteilung für den Münzwurftest.
Rechts: Z-transformierte Normalverteilung = Standardnormalverteilung. Diese Verteilung wird tabelliert, um die Verwerfungsgrenzen abzulesen.
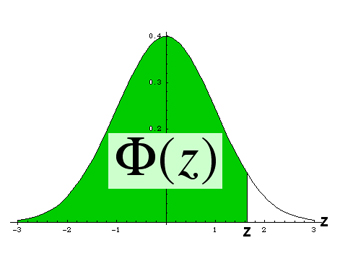
Oben: In den gängigen Tabellen wird zur vorgewählten Fläche Φ(z) der Standardnormalverteilung der zugehörige z-Wert aufgeführt. Soll z.B. die Restfläche rechts (weiss) 2.5% betragen, so beträgt Φ(z) 97.5% oder 0.9750. In der Tabelle liest man den zugehörigen z-Wert als z = 1.96 ab.
Die Zufallsvariable X wird mittels folgender Z-Transformation (s. auch Wahrscheinlichkeit02) flächentreu auf Standardnormalform gebracht. Diese Form ist in Formelsammlungen tabelliert. Zur grünen Fläche (s. Bild links) kann der zugehörige z-Wert abgelesen werden (und umgekehrt). Hat man den z-Wert ermittelt, wird x durch Rücktransformation zurückgewonnen.
Z-Transformation der Zufallsvariablen X: Z = (X - μ) / σ Rücktransformation: X = μ + σZ |
Einige häufig gebrauchte Werte:
| Φ(z) | z |
| 0.9500 | 1.645 |
| 0.9750 | 1.960 |
| 0.9900 | 2.326 |
Beispiel: Unser Münzentest (50-mal Münzwurf): Ermittlung des Verwerfungsbereichs bei gegebenem Signifikanzniveau:
Angenommen, wir möchten diesmal den Test auf dem 5%-Signifikanzniveau durchführen und zwar zweiseitig. Wir müssen also auf jeder Seite der Glockenkurve 2.5% der Fläche abschneiden. Wenn wir rechts 2.5% abschneiden, ergibt sich die grüne Fläche zu 0.9750. Die Tabelle liefert z* = 1.96. Das ist die rechte Verwerfungsgrenze, die rechts 2.5% abschneidet.
Die Rücktransformation liefert x = √12.5⋅1.96 + 25 ≈ 31.93. Das ergäbe einen Annahmebereich von ca. [18.07; 31.93] oder -leicht vergrössert und ganzzahlig -
[18; 32]. Der Verwerfungsbereich ergibt sich so wieder als V = {0, ..., 17, 33, ... , 50}.
Vergleich exakte Binomialverteilung / Näherung durch Normalverteilung mit Annahmebereich [18;32]:
Exakte Binomialverteilung: α = 3.28%; Normalverteilung: α = 4.78%. Es ist klar, dass wegen der Unstetigkeit der Binomialverteilung und der Stetigkeit der Normalverteilung ein kleiner Fehler entstehen muss.
Man kann den Fehler durch eine "Stetigkeitskorrektur" etwas mildern.
Statt z* = (x - μ ) / σ wählt man z* = (x - μ + 0.5 ) / σ. Für x = 32 erhalten wir dann in unserem Beispiel z* = (32-25+0.5)/√12.5 = 2.12. Der zugehörige Flächenwert ist 98.3%, d.h. auf jeder Seite werden 1.7% abgeschnitten, insgesamt also α = 3.4%. Das ist bereits eine bessere Näherung als α = 4.78%.
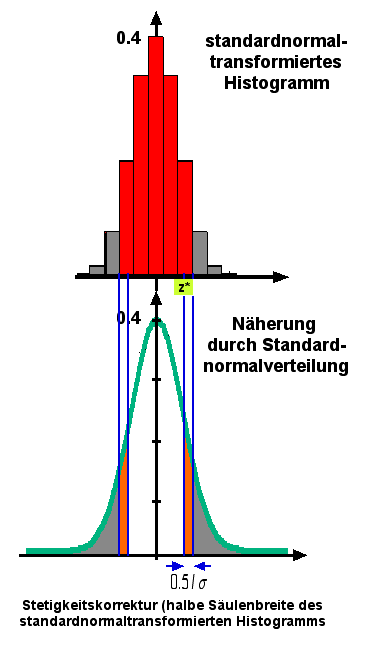
Stetigkeitskorrektur beim Ersetzen der Binomialverteilung durch die Normalverteilung:
Voraussetzung ist npq ≥ 9.
Bild rechts: Mehrmaliger Münzwurf. Das Histogramm, welches die "Anzahl Köpfe" in n Würfen zeigt, wird standardnormal-transformiert. Grau: Ablehnungsbereich.
Unten: Näherung durch die Standardnormalverteilung.
Der kritische z*-Wert wird bei der Gaussglocke um eine halbe Säulenbreite des standardnormierten Histogramms verschoben (siehe Bild unten). Damit wird die rote Fläche im Histogramm oben besser berücksichtigt.
Weiterere Signifikanztests
Quelle: Dr. Robert Ineichen: Elementare Beispiele zum Testen statistischer Hypothesen, Orell Füssli-Verlag, Zürich, 2. Auflage, 1978, vergriffen, p.21 ff
1. Ein Apparat zeigt positive (+) und negative (-) Abweichungen vom Sollwert. Uns interessiert nur die Richtung der Abweichungen, nicht aber deren Betrag. Die einzelnen Abweichungen seien unabhängig voneinander. Man will testen, ob die Wahrscheinlichkeiten für positive und negative Abweichungen voneinander verschieden sind.
Wie könnte ein Test-Design auf 5%-Signifikanzniveau aussehen?
Lösungsmöglichkeit:
H0: P(+) = 0.5
H1: P(+) ≠ 0.5 (zweiseitiger Test)
Beispiel: 20 Messungen
Testgrösse: Anzahl (+)Abweichungen
Verwerfungsbereich: Wir probieren mit Hilfe eines Rechners und finden mit
V = {0, 1, 2, 3, 4, 5, 15, 16, 17, 18, 19, 20} ein α von ca. 4.1% (Binomialverteilung).
Falls wir also zwischen 6- und 14-mal eine (+)Abweichung finden, behalten wir H0 bei, andernfalls verwerfen wir die Nullhypothese.
Vorzeichentest für einen Vergleich aus gepaarten Stichproben In gleicher Art wie in Beispiel 1 kann etwa folgendes getestet werden: Anmerkung: Solche Vorzeichentests können auch mit Ordinalskalen (qualitative Skalen, die lediglich eine Reihenfolge festlegen) durchgeführt werden. In Wirklichkeit sind ja Aufsatz-Stilnoten eher ordinale (und damit qualitative und nicht quantitative) Daten. |
2. Das Statistische Jahrbuch der Schweiz 1972 zeigte für die Zeit zwischen 1969 und 1976 n = 91'342 Geburten, davon x = 47'179 Knabengeburten. Sei X die Anzahl Knabengeburten. Nullhypthese: P(Knabengeburt) = 0.5, Alternativhypothese: P(Knabengeburt) > 0.5, also einseitiges Testdesign (aufgrund von Vorwissen). Signifikanzniveau: 5%. Man designe den Test (Normalverteilung).

Lösung:
Erwartungswert bei Nullhypothese: 91'342*0.5 = 45'671 Knabengeburten = μ.
σ = √(n*0.5*0.5) = 151.11.
z-Transformation von x = 47'179:
z = (47'179 -
45'671) / 151.11 ≈ 10.0. Gemäss Tabelle liegt die z-Verwerfungsgrenze zum Niveau 5% rechts bei 1.645. Unser z-Wert 10.0 liegt somit rechts davon, also im Verwerfungsbereich von H0: Wir verwerfen also die Nullhypothese, wonach Knabengeburten die Wahrscheinlichkeit 0.5 haben zugunsten der Alternativhypothese P(Knabengeburt) > 0.5. Sogar auf dem Signifikanzniveau 1% (z-Verwerfungsgrenze = 2.326) muss H0 verworfen werden (man spricht in diesem Fall von hochsignifikanter Abweichung).
3. Wir finden aufgrund statistischer Zahlen einen Schätzwert für P("Knabengeburt"), nämlich 0.514. Ist P("Knabengeburt") von diesem Schätzwert verschieden?
Man teste zweiseitig mit Hilfe der Zahlen der Aufgabe 2.
Lösung:
H0: p = 0.514
H1: p ≠ 0.514
μ = 0.514*91'342 = 46'949.788
σ = √(0.514*0.486*91'342) = 151.055
Z-Transformation von x = 47'179:
z = (47'179 -
46'950) / 151.055 ≈ 1.516.
Wir testen zweiseitig auf dem 5%-Niveau, d.h. wir schneiden auf jeder Seite der Glockenkurve je 2.5% ab. Die Tabelle oben zeigt für die Verwerfungsgrenze den z-Wert 1.960. Unser gefundenes z = 1.516 befindet sich links dieser Grenze im Annahmebereich. Wir behalten also
H0 bei, d.h. die Hypothese, dass P("Knabengeburt") = 0.514 sei.
These: Signifikanz bedeutet nicht unbedingt klinische Relevanz! |
Bei genügend hoher Stichprobengrösse ist praktisch jede Nullhypothese chancenlos. Ein klinisch oder gesellschaftlich völlig irrelevanter Unterschied kann bei stark aufgeblähter Stichprobengrösse statistisch als hochsignifikant erscheinen. Ein Beispiel:
Nehmen wir an, die Forschung zeige, dass bei über 50-jährigen Personen eines bestimmten Gebietes mit 30%-iger Wahrscheinlichkeit Blutdruckprobleme vorhanden sind. Nun definiert ein Forschungsteam gewisse Elemente E gesunden Lebensstils und möchte zeigen: Bei den Personen mit E treten Blutdruckprobleme weniger stark auf. Aufgrund des Vorwissens wird einseitig getestet, da E nach aktuellem Wissensstand Blutdruckprobleme sicher nicht verstärkt.
Nehmen wir für unser Modellbeispiel nun aber an, dass der tatsächliche Effekt der Elemente E klinisch und praktisch nur sehr gering sei, dass z.B. immer noch 28% der über 50-jährigen mit gesundem Lebensstil E Blutdruckprobleme aufweisen.
(Die Gründe für den geringen Einfluss von E können vielfältig sein: Drittfaktoren wie Umweltbelastungen, die E entgegenwirken, genetische Veranlagungen, nicht optimale Auswahl von E, usw.)
Mit einer bombastisch hohen Stichprobengrösse kann das Forschungsteam trotzdem die Nullhypothese "E hat keinen signifikanten Einfluss auf die Blutdruckprobleme" widerlegen.
Die Rechnung geht so:
a) Sei n = 10'000 eine bombastische Stichprobengrösse von Personen mit Lebensstil E.
Nullhypothese: P(Blutdruckprobleme trotz Lebensstil E) = p = 0.3. Alternativhypothese: p < 0.3.
Die Binomialverteilung mit p = 0.3 und n = 10'000 ergibt einen Mittelwert von 3'000 und eine Varianz von 2'100, also eine Standardabweichung von etwa 46.
Wegen n⋅p⋅(1-p) >> 9 kann die Binomial- durch die Normalverteilung ersetzt werden.
Wir schneiden links der Normalverteilung 5% der Fläche ab und erhalten als kritische Grenze
3000 - 1.645⋅46 = 2924.
Finden wir weniger als 2924 Personen mit Lebensstil E, verwerfen wir die Nullhypothese. Unter dem praktisch und klinisch relativ unbedeutenden Erfolgseffekt von E mit p = 0.28 finden wir jedoch mit 99.7% Wahrscheinlichkeit, also fast sicher, tatsächlich weniger als 2924 Personen in unserer Stichprobe. Die Nullhypothese wird somit fast sicher signifikant* verworfen, obwohl Lebensstil E das Blutdruckrisiko lediglich von 30% auf 28% senkt. Wer Lebensstil E vermarkten will, wird diesen bescheidenen Effekt natürlich verschweigen und auf den signifikanten Test verweisen.
(*Sogar ein hochsignifikantes Verwerfen der Nullhypothese ist bei dieser riesigen Stichprobengrösse wahrscheinlich: Abschneiden von 1% links der Normalverteilung: Wir landen immer noch mit 98% Wahrscheinlichkeit im Ablehnungsbereich der Nullhypothese.)
b) Wird im Gegensatz zu oben die Stichprobengrösse viel kleiner, z.B. n = 50, gewählt, so liegt bei einem Signifikanzniveau von 5% die kritische Grösse bei 9. Man wird jedoch unter den 50 Personen mit Lebensstil E mit grosser Wahrscheinlichkeit (92.6%) mehr als 9 Personen mit Blutdruckproblemen finden und somit die Nullhypothese beibehalten: "kein signifikanter Einfluss von E auf Blutdruckprobleme".
Fazit: Die Stichprobengrösse entscheidet mit über Beibehaltung oder Ablehnung einer Nullhypothese.
Bortz / Schuster, Statistik, 7. Auflage, Springer 2010, p.112, schreiben:
"Den Wert einer empirischen Forschungsarbeit allein davon abhängig zu machen, ob das Untersuchungsergebnis statistisch signifikant ist oder nicht, wird von vielen Autoren vehement kritisiert (...). Manche Autoren gehen sogar so weit, mangelnden Fortschritt in der psychologischen Forschung der ausschliesslichen Verwendung von Signifikanztests anzulasten. (...) Die korrekte Anwendung eines Signifikanztests und die Interpretation der Ergebnisse unter dem Blickwinkel der praktischen Bedeutsamkeit sind essentielle und gleichwertige Bestandteile der empirischen Hypothesenprüfung."
"Statistisch signifikant" muss nicht unbedingt auch "klinisch relevant" bedeuten!
Im Beispiel oben erkannte Test a) mit n = 10'000 auch einen kleinen Effektunterschied als signifikant, während Test b) mit n = 50 diese eher bescheidene Differenz als nicht signifikant einstufte. Die Teststärke bei b) war geringer als bei a).
Die Bedeutsamkeit eines Effektunterschieds muss "ausserstatistisch" festgelegt werden (medizinische, wirtschaftliche, ethische ... Überlegungen).
Nehmen wir im Beispiel oben einmal an, wir erachteten einen Anteil von 25% bei Personen mit gesundem Lebensstil E als bedeutsamen Effektunterschied (gegenüber 30% der Normalbevölkerung über 50). Dies rechtfertige dann z.B. den Kostenaufwand einer breiten Gesundheitskampagne.
Wir benötigen dann eine daran angepasste Teststärke, welche diesen Effektunterschied erkennt, kleinere Unterschiede jedoch als nicht signifikant taxiert.
Wenn wir auf dem 5%-Signifikanzniveau arbeiten wollen: Welche Stichprobengrösse wäre dann adäquat?
Wir finden eine Stichprobengrösse von n = 859.3 (oder ca. 860) als adäquaten Wert (Rechnung rechts), d.h. wir untersuchen eine Stichprobe von 860 Personen mit gesundem Lebensstil E und eruieren die Anzahl x der Personen, die trotz Lebensstil E Blutdruckprobleme haben.
Der kritische Wert bei einem Signifikanzniveau von 5% und p = 0.3 liegt dann bei x = 235.6.
Finden wir 235 Personen oder weniger, verwerfen wir die Nullhypothese zugunsten der These "E wirkt in dem von uns als bedeutsam festgelegten Ausmass".
In der Stichprobe der 860 Personen mit Lebensstil E wird man dann, falls p = 0.25 tatsächlich gelten sollte, mit einer Wahrscheinlichkeit von lediglich ca. 5% 236 oder mehr Personen finden, die immer noch Blutdruckprobleme haben und dann die Nullhypothese ("E wirkt nicht oder nur unbedeutend") fälschlicherweise beibehalten (Fehler 2. Art).
Mit einer Wahrscheinlichkeit von ca. 95% werden wir also beim Vorhandensein eines Effekts, den wir als bedeutsam definiert haben die Nullhypothese zu Recht verwerfen, d.h. unser Test hat die richtige Sensitivität. Wir sprechen von einer Teststärke (Testsensitivität, Trennschärfe) von 95%.
Rechnung:
Verteilung mit p = 0.3: Mittelwert = 0.3n, Varianz = 0.3⋅0.7⋅n, Standardabweichung = 0.458⋅√n.
Kritische Grenze k bei 5% Signifikanzniveau: k = 0.3n - 1.645⋅0.458√n.
Verteilung mit p = 0.25: Mittelwert = 0.25n. Varianz = 0.25⋅0.75⋅n, Standardabweichung = 0.433⋅√n.
Gleichung: k = 0.3n - 1.645⋅0.458√n = 0.25n + 1.645⋅0.433⋅√n. Lösung: n = 859.3 oder ca. 860.
Die konkreten Werte mit n = 860:
Verteilung mit p = 0.3: Mittelwert = 258, Standardabweichung = 13.43
kritische Grenze k = 236
Verteilung mit p = 0.25: Mittelwert = 215, Standardabweichung = 12.70
(236 - 215)/12.70 = 1.65; entspricht der 95%-Grenze.

Rot: Nullhypothese; roter 5%-Bereich = α
= Wahrscheinlichkeit eines Fehlers 1. Art, d.h. Ablehnung der Nullhypothese, obwohl diese zutrifft.
Blau: Verteilung, falls p = 0.25; blauer 5%-Bereich = β = Wahrscheinlichkeit eines Fehlers 2. Art, d.h. irrtümliche Beibehaltung der Nullhypothese.
1 -
β = Teststärke (Testsensitivität) = Wahrscheinlichkeit, die Alternative anzunehmen, wenn diese auch zutrifft. Hier 95%.
Berechnung der adäquaten Stichprobengrösse bei einer gewünschten Teststärke von 90% und gegebenem Alternativ-Szenario:
Welche Stichprobengrösse ist adäquat, wenn auf dem 5%-Signifikanzniveau bei obigem Beispiel eine Teststärke von 90% für das Alternativszenario p = 0.25 erreicht werden soll?
Wie oben gilt für die Nullhypothesen-Verteilung: k = 0.3n - 1.645⋅0.458√n.
(5%-Signifikanz-Niveau.)
Alternativ-Verteilung p = 0.25: s = 0.433⋅√n. k = 0.25n + 1.282⋅0.433⋅√n.
(Schneidet rechts 10% Fläche ab. Die Zahl 1.282 kann in einer Tabelle oder auf Taschenrechnern mit Statistikfunktionen [Invers Normalverteilung] abgelesen werden.)
Gleichung:
0.3n - 1.645⋅0.458√n = 0.25n + 1.282⋅0.433⋅√n
=> 0.05n = 1.309⋅√n => 0.05⋅√n = 1.309 => √n = 26.170 => n = 685.
Geogebra-Modell zur Teststärke

Grafik: Teststärke 1-β in Abhängigkeit der Alternativ-Wahrscheinlichkeit p. n = 400, α = 0.05. Für p<0.18 ist die Teststärke beinahe 1, die Wahrscheinlichkeit eines Fehlers 2.Art somit praktisch null.
Das Geogebra-Modell zeigt anschaulich, wie diese Funktionswerte entstehen.
Erläuterung zum Geogebra-Modell:
Wir betrachten immer noch das hypothetische Beispiel oben.
Rote Normalverteilungskurve: Nullhypothese: p = 0.3.
Diesmal sei die Stichprobengrösse mit n = 400 gegeben. Kritischer 5%-Wert bei k = 105:
Finden wir unter den 400 Personen mit Lebensstil E weniger als 105 Personen mit Blutdruckproblemen, verwerfen wir die Nullhypothese auf 5%-Niveau.
Bei welchem Alternativ-Szenario (blaue Farbe, p einstellbar mit Regler) ist welche Teststärke 1-β bzw. welche Wahrscheinlichkeit β eines Fehlers 2.Art zu erwarten?
Wir sehen z.B., dass bei p = 22.8% die Teststärke 95% (bzw. die Wahrscheinlichkeit eines Fehlers 2.Art 5%) beträgt. Möchten wir den Test sensitiver machen, müssen wir wie im Beispiel oben die Stichprobengrösse n erhöhen.
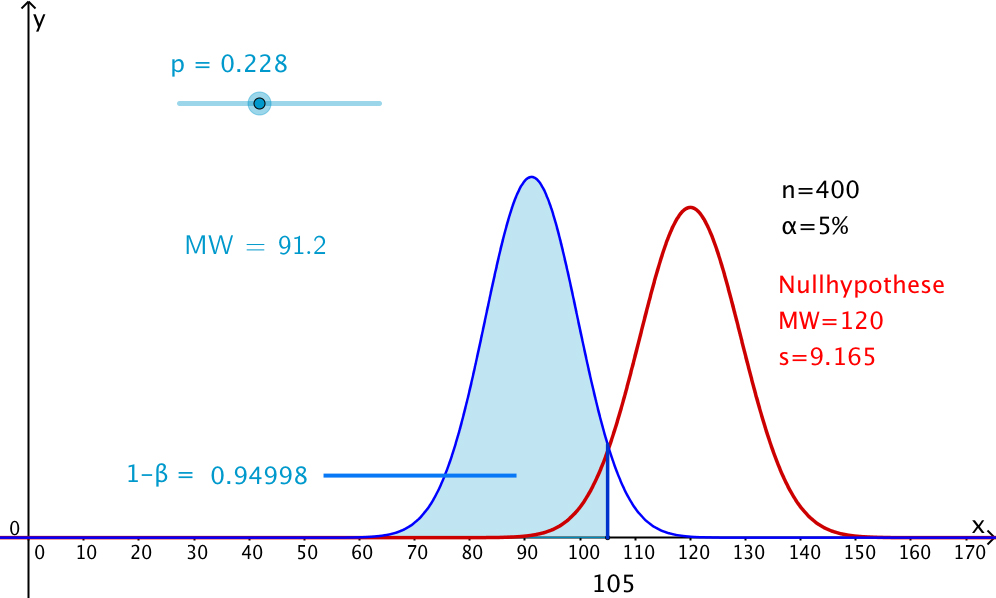
Abb: Ein Beispielbild aus der Geogebra-Simulation: p = 22.8%
Oft begnügt man sich mit einer Wahrscheinlichkeit für einen Fehler 2. Art, die das Vierfache von α ist, hier also mit β = 20%. Dann zeigt das Geogebra-Modell (oder die Grafik links) ein p von 24.4% als Szenario, für das der Test mit diesen Kennzahlen und dieser Stichprobengrösse geeignet ist.
Regler p erzeugen (min 0.18, max 0.3, Schrittweite 0.0002).
f(x) = Normal[400p, (400p(1-p))^0.5,x]; erzeugt die Normalverteilung des Alternativ-Szenarios mit Wahrscheinlichkeit p.
Integral[f,-1000,105]; ergibt die Zahl a. (Eigentlich müsste von -∞ bis 105 integriert werden; -1000 als untere Integrationsgrenze genügt jedoch.) a ist der zu p gehörende gesuchte Funktionswert.
A(p,a); ergibt einen Punkt A des gesuchten Graphen. Für diesen Punkt "Spur ein" wählen.
Regler p laufen lassen. A wandert und erzeugt als Spur den Graphen der gesuchten Funktion.
Das Analogon zum Mittelwert einer Stichprobe ist der Erwartungswert einer Zufallsvariablen. Die Parameter der Stichprobe werden gewöhnlich mit lateinischen, diejenigen der Grundgesamtheit mit griechischen Buchstaben bezeichnet.
Hier die Formeln für Erwartungswert und Varianz einer Zufallsvariablen mit k möglichen Ausprägungen repektive für den stetigen Fall:
 |
 |
Würfelsimulation einer Verteilung mit vorgegebenem Mittelwert μ und vorgegebener Standardabweichung σ

Aufgabe:
Man wirft 6 gewöhnliche Spielwürfel (Zahlen 1 bis 6) und bildet die Augensumme. Dies sei die Zufallsgrösse X.
Man berechne aufgrund obiger Definitionen Erwartungswert und Varianz bzw. Standardabweichung von X.
Lösung:
Sei Xi = gewürfelte (oben liegende) Augenzahl des i-ten Würfels.
Der Erwartungswert für Xi ist 3.5. Der Erwartungswert für X (als Summe der sechs Xi ) ist
6⋅3.5 = 21.
Die Varianz der Zufallsvariablen "gewürfelte Augenzahl eines Würfels" ist gemäss obiger Definition gleich
(1/6)⋅[(1-3.5)2+(2-3.5)2+(3-3.5)2+(4-3.5)2+(5-3.5)2+(6-3.5)2] = 17.5 / 6.
Die Varianz von X (als Summe der 6 unabhängigen Xi ) ist 6⋅17.5 / 6 = 17.5. Die Standardabweichung von X ist demzufolge gleich √17.5 = 4.183.
Wir bilden nun aus X die Grösse Z:
Z = (X - 21) ⋅(σ / 4.183) + μ
Lässt man nun sehr viele Personen (n Personen) je diese Grösse Z erwürfeln (zuerst Summe der 6 gewürfelten Zahlen bilden -> X und daraus Z berechnen) , so ist die Verteilung von Z annähernd μ - σ -verteilt (mit 6 Würfeln entsteht jedoch keine perfekte Normalverteilung).
Für eine perfektere Verteilung, die einer Normalverteilung näher käme, müsste man mit mindestens 25 Würfeln die Augensummen bilden (vgl. zentraler Grenzwertsatz unten).
Auf diese Weise lassen sich im Statistikunterricht Rollenspiele durchführen. So kann man sich etwa einen "Intelligenzquotienten" erwürfeln (μ = 100, σ = 15) und die Verteilung studieren. Hier 4 Beispiele aus solchen Zufallswürfen:
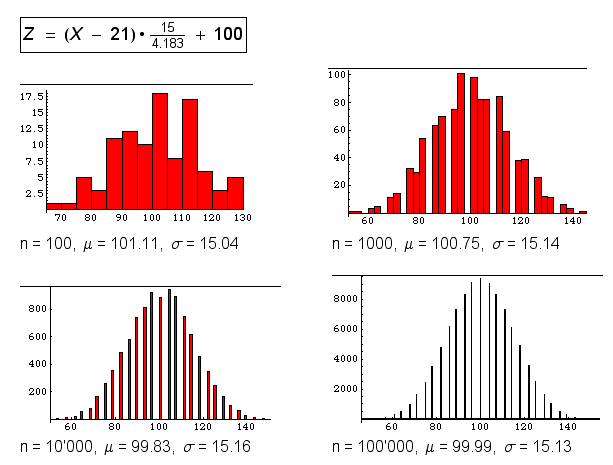
Abb. oben: Simulation einer 100-15-Verteilung durch Werfen von 6 Würfeln und Addition der Augenzahlen -> X. Die Grösse Z entsteht wie folgt:
Z = (X - 21)⋅(15 / 4.183) + 100.
n = Anzahl Würfe mit 6 Würfeln.
n = 100, n = 1000, n = 10'000, n = 100'000.
Warnung vor einem Trugschluss: Bei einer grossen Anzahl von Auswertungen (z.B. 100'000) entsteht nicht zunehmend eine Normalverteilung, sondern es entsteht zunehmend die Idealverteilungsform für die Zufallsvariable "Augensumme aus 6 Würfeln", d.h. die relative Häufigkeit nähert sich zusehends "fast sicher" der theoretischen Wahrscheinlichkeit. 6 Würfel als Augensummen-Lieferanten ergeben noch keine sehr gute Normalverteilungs-Näherung. Dafür wären mindestens 25 Würfel erforderlich.
Ein hervorragendes Buch mit solchen Simulationsideen ist:
Andrew Gelman, Deborah Nolan: Teaching Statistics - a bag of tricks. Oxford University Press, 2002, ISBN 0 19 857224 7.
Das dargelegte Beispiel wird dort beschrieben. Allerdings lassen Gelman/Nolan ihre Studierenden mit einem Ikosaederwürfel würfeln, auf dem jede Ziffer von 0 bis 9 je doppelt aufgedruckt ist. Die Zahlen für Mittelwert und Standardabweichung sind dann andere (welche?).
Nun erfinden wir ein rein äusserliches Merkmal, jedoch so, dass dieses Merkmal die hohen IQs von den tiefen recht auffällig trennt (ein solches Merkmal, z.B. Sitzordnung, Brillenträger, usw.) lässt sich mit etwas Fantasie fast immer nachträglich finden, wenn man "kreativ genug" sucht.
Haben nun Personen mit diesem Merkmal tatächlich einen höheren IQ? - Natürlich nicht, denn wir haben in unserem Rollenspiel die "IQs" ja erwürfelt. - Wir sehen also: Sortieren der Daten nach einem nachträglich gesuchten Merkmal darf auf keinen Fall praktiziert werden, das ist ohne jeden wissenschaftlichen Wert. Eine Hypothese muss vorher aufgestellt und das Experiment daraufhin geplant werden. Beim Interpretieren bestehender Daten ist also äusserste Vorsicht geboten.
Aufgabe
Man würfelt mit zwei gewöhnlichen Spielwürfeln und bildet die Augensumme.
a) Man berechne Erwartungswert und Varianz bzw. Standardabweichung der Zufallsgrösse "Augensumme".
b) Man modelliere aus der Augensumme X eine Grösse Z mit Erwartungswert 12
und Varianz 8.
Lösung:
a)
Erwartungswert der Augensumme zweier Würfel: 2⋅3.5 = 7.
Varianz der Zahlen eines einzelnen Würfels (s. oben): 17.5/6;
Varianz der Augenzahlensumme von zwei Würfeln: 17.5/6 + 17.5/6, somit:
Varianz: 2⋅17.5/6 = 5.833...; Standardabweichung = 2.415
b)
Z = (X - 7)⋅(√8 / 2.415) + 12 oder Z = (X - 7)⋅1.171 + 12

oben: Verteilung der Zufallsvariable "Augensumme aus 2 Würfeln".
Die Verteilung ist weit entfernt von einer Normalverteilung.
rechts: Verteilung der Zufallsvariable "Augensumme aus 3 Würfeln":
Es entsteht immer noch keine Normalverteilung, eine glockenförmige Wölbung wird jedoch bereits sichtbar. Um eine ungefähre Normalverteilung zu erreichen, müsste man mit etwa 25 Würfeln Augensummen würfeln (siehe unten: zentraler Grenzwertsatz). Für unser IQ-Experiment oben genügen jedoch 6 Würfel durchaus.

Hier die Wahrscheinlichkeitsverteilungen für die Augensummen von mehreren Würfeln.
Quelle:
https://www.rechner.club/wahrscheinlichkeit/wuerfelsumme-tabelle
Man erkennt, wie sich die Diagrammform langsam einer Normalverteilungsglocke annähert.
Ab etwa 25 Würfeln pro Wurf, von denen man die Augensumme bildet kann man von einer guten Normalverteilungs-Näherung sprechen.

Anwendung der Rechenregeln für Erwartungswert und Varianz:
Zwei relative Häufigkeiten aus zwei unabhängigen Stichproben
Quelle: R. Ineichen, s. oben
Zwei verschiedene Anlagen produzieren dasselbe Objekt. Man vermutet, dass die Prozentsätze an Ausschuss auf den Anlagen verschieden sind und will dies testen.
Man entnimmt Anlage 1 eine Stichprobe von n1
= 200 Stück und findet k1 = 5 fehlerhafte Stücke; Anlage 2 entnimmt man n2 = 100 Stück und findet k2 = 10 fehlerhafte Stücke. Sind die beiden Ausschusswahrscheinlichkeiten p1 und p2 wirklich verschieden?
Wir testen zweiseitig auf 5%-Niveau.
Lösung:
p1 und p2 sind unbekannt. Die Stichproben sind unabhängig entnommen und gross genug. Es seien X = k1 / n1 und Y = k2 / n2 die betrachteten Zufallsvariablen, die von der Stichprobe abhängen. Wir betrachten die Zufallsvariable X - Y. Sie ist bei genügend grosser Stichprobe normalverteilt.
Die Nullhypothese lautet: p1 = p2.
Es ist E(X) = p1 und E(Y) = p2 und folglich E(X - Y) = E(X) - E(Y) = p1 - p2.
Unter der Nullhypothese ist also E(X - Y) = 0.
Die Alternativhypothese ist p1 ≠ p2.
Es ist Var(X) = Var((1/n1)k1)= (1/n12) n1 p1 (1 - p1) = p1 (1 - p1) / n1 und analog
Var(Y) = p2 (1 - p2) / n2 (s. Rechenregeln für die Varianz oben).
Folglich ist Var(X - Y) = Var(X) + Var(Y) (wegen der Unabhängigkeit) =
p1 (1 - p1) / n1 + p2 (1 - p2) / n2.
Unter der Nullhypothese ( p2 = p1) wird dies zu p1(1 - p1)(1/n1 + 1/n2).
Leider ist p1 ja unbekannt. Wir ersetzen diesen Wert durch einen Schätzwert, nämlich durch das gewichtete Mittel der beiden relativen Häufigkeiten, d.h. durch
(5 + 10) / (200 + 100) = 15 / 300 = 0.05 = p.
Dann wird Var(X - Y) = 0.05*0.95*(0.005 + 0.010) = 0.0007125.
Nun können wir mit E(X - Y) = 0 und Var(X - Y) = 0.0007125 die Z-Transformation vornehmen und erhalten
z =(5/200 - 10/100 - 0) / √(0.0007125) = -2.81.
Dieser Wert liegt links der linken Verwerfungsgrenze -1.96, also im Verwerfungsbereich.
Wir verwerfen also die Nullhypothese und stützen die Alternativhypothese ungleicher Ausschusswahrscheinlichkeiten.
Wenn wir einer Grundgesamtheit mit Erwartungswert μ und Varianz σ2 eine Stichprobe der Grösse n entnehmen, so kommt diese durch Zufallsauswahl zustande. Diese Stichprobe besitzt einen bestimmten Mittelwert. - Eine andere Stichprobe der Grösse n wird einen leicht andern Mittelwert aufweisen. Jede Stichprobe wird diesbezüglich etwas variieren. Die Mittelwerte einer Stichprobe sind also abhängig von der Zufallsauswahl der Stichprobe, sind somit Zufallsvariable. Als solche haben sie selber einen Erwartungswert und eine Varianz.
Es dürfte plausibel sein, dass der Erwartungswert der verschiedenen Stichprobenmittelwerte gleich μ ist.
Mit der Varianz ist es nicht so einfach. Plausibel ist, dass die Mittelwerte vieler verschiedener Stichproben der Grösse n weniger streuen als die ursprünglichen Daten selber; die Mittelwerte gleichen ja Extremschwankungen bereits aus. Ohne Beweis geben wir an: Die Varianz der verschiedenen Stichproben-Mittelwerte ist gleich σ2 / n.
Zusammengefasst haben wir folgende Formeln:

Das Gesetz der grossen Zahlen besagt nun:
- Mit wachsender Stichprobengrösse n nähert sich der Stichprobenmittelwert dem Erwartungswert μ der Grundgesamtheit. (Schwaches Gesetz der grossen Zahlen) Oder:
- Der Stichprobenmittelwert ist bei wachsendem n "fast sicher" "sehr nahe" am Erwartungswert μ der Grundgesamtheit; je grösser n, desto mehr nähert sich diese Wahrscheinlichkeit dem Wert 1. (Starkes Gesetz der grossen Zahlen)
Ein Gesetz der grossen Zahlen von Jakob Bernoulli (1654 - 1705)
Ein Bernoulli-Versuch (Versuch mit zwei möglichen Ausgängen: "Treffer" oder "Niete", mit P("Treffer") = p und P("Niete") = (1 - p) = q) wird n-mal wiederholt (Bernoulli-Kette). Sei X die Zufallsvariable "Anzahl Treffer in n Versuchen". X / n ist dann die relative Häufigkeit der Treffer in n Versuchen.
Der Satz von Bernoulli sagt: X / n unterscheidet sich bei genügend grossem n "fast sicher" um "sehr wenig" vom theoretischen Wahrscheinlichkeitswert p. D.h. X / n kann fast sicher als gute Näherung für p angesehen werden, wenn n genügend gross ist.
Konkret:
![]()
Beispiel:
In einer Produktion beträgt der Anteil einwandfreier Produkte 90%. Man entnimmt eine Stichprobe von 1'000 Stück. Man darf in dieser Probe also etwa 900 einwandfreie Stücke erwarten, vielleicht etwas mehr, vielleicht etwas weniger. Mit welcher Wahrscheinlichkeit findet man in dieser Stichprobe zwischen 875 und 925 einwandfreie Stücke, also eine Abweichung vom Sollwert 900 um maximal 25 Stück oder 2.5%?
Lösung:
Es ist ε = 0.025. Der Satz von Bernoulli liefert:
P( |X/1000 - 0.9| < 0.025) ≥ 1 - (0.9*0.1)/(0.0252 *1000) = 0.856 = 85.6%.
Mit einer Wahrscheinlichkeit von 85.6% liegt die Zahl der einwandfreien Stücke in der Stichprobe im Vertrauensintervall [875; 925].
Zusatzfrage: Wie gross muss die Stichprobe gewählt werden, damit die Wahrscheinlichkeit für Werte in obigem Vertrauensintervall 95% beträgt?
Antwort: n = 2880 Stück.
Man erkennt: Je grösser n gewählt wird, desto mehr nähert sich die berechnete Wahrscheinlichkeit dem Wert 1.
Anmerkung: Wenn p und q unbekannt sind, kann eine grobe Schätzung so stattfinden: p⋅q ist maximal 1/4, nämlich für p = q = 1/2. In allen andern Fällen ist p⋅q < 1/4. Wir können also anstelle von p⋅q den Wert 1/4 einsetzen und erhalten damit eine -relativ grosszügige- Schätzung.
Beispiel:
Man führt vor einer Abstimmung eine Meinungsumfrage durch (Stichprobe n Stimmwillige) und ermittelt X/n = Ja-Anteil. Wie gross ist n zu wählen, wenn man mit max. 5% Abweichung die Wahrscheinlichkeit p = P("Ja") ermitteln will und dies mit einer "Sicherheit" von 95%?
Lösung:
P( |X/n - p| < 0.05) ≥ 1 - 0.25/(0.0025⋅n) = 0.95.
Es folgt 0.25/(0.0025*n) = 0.05 und somit n = 2'000.
Das bedeutet: Das Vertrauensintervall [X/n - 0.05 ; X/n + 0.05] überdeckt mit einer Wahrscheinlichkeit von 95% das gesuchte p("Ja"), wenn wir X/n mittels einer Stichprobe der Grösse 2'000 ermitteln. Sprechen sich z.B. 1200 Personen in der Stichumfrage für ein "Ja" aus, wird X/n = 1200/2000 = 0.6. Das Intervall [0.55; 0.65] oder [55%; 65%] überdeckt mit 95%-iger Wahrscheinlichkeit den Wahrscheinlichkeitswert p für ein Ja.
Wir formulieren hier nur die schwache Form des zentralen Grenzwertsatzes für unabhängige und identisch verteilte Zufallsvariable, d.h. für Zufallsvariable Xi , die alle den gleichen Erwartungswert μ und die gleiche Varianz σ2 haben und die unabhängig voneinander sind . Der zentrale Grenzwertsatz besagt nun, dass die Summe solcher Xi asymptotisch normalverteilt ist mit Erwartungswert n⋅μ und Varianz n⋅ σ2 .
(Die starke Form des zentralen Grenzwertsatzes gilt unter nicht sehr einschränkenden Zusatzbedingungen auch für nicht identisch verteilte Zufallsvariable Xi .)
Unterwerfen wir die Summe der Xi der Z-Transformation, so sieht die Sache so aus:
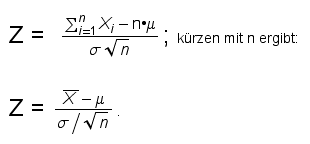
Insbesondere sind also die Mittelwerte der möglichen Stichproben des Umfangs n aus derselben Grundgesamtheit normalverteilt mit Erwartungswert μ und Varianz σ2/n.
Dies gilt auch dann, wenn die Grundgesamtheit nicht normalverteilt ist. n sollte ≥ 25 sein.
Beispiel 1: Stichprobenmittelwerte sind für hinreichend grosse Stichprobenumfänge n normalverteilt
Das Körpergewicht einer bestimmten Personenkategorie habe einen Erwartungswert von 72 kg bei einer Standardabweichung σ von 8 kg.
Wir entnehmen nun etliche Stichproben des Umfangs n = 30 und bestimmen die Mittelwerte davon. Diese werden variieren. Nach dem zentralen Grenzwertsatz sind sie normalverteilt mit Erwartungswert 72 kg und Standardabweichung (8 / √30)kg = 1.46 kg.
Für z = ±1.96 werden in der Standardnormalverteilung links und rechts je 2.5% der Fläche abgetrennt. Die Rücktransformation X = μ + σZ ergibt
(72 ± 1.96⋅1.46) kg als 95%-Bereich, also das Intervall [69.14 kg; 74.86 kg] . Man wird also in einer Stichprobe des Umfangs n = 30 mit 95%-iger Wahrscheinlichkeit einen Mittelwert zwischen 69.14 kg und 74.86 kg erhalten.
Beispiel 2: Binomialverteilte Zufallsvariable X als Summe von identisch verteilten Zufallsvariablen Xi
Wir würfeln 100-mal mit einem gewöhnlichen Spielwürfel. Wir definieren die Zufallsvariable Xi , die sogenannte "Zählvariable":
Xi = 1, wenn im i-ten Wurf eine Sechs gewürfelt wurde, andernfalls sei Xi = 0.
Alle Xi haben Erwartungswert 1⋅(1/6) ≈ 0.167 und Varianz 1⋅(1/6)⋅(5/6) ≈ 0.139.
Sei X = ∑Xi . X ist also die Zufallsvariable "Anzahl gewürfelter Sechsen in 100 Würfen". Als Summe der Xi ist X annähernd normalverteilt mit Erwartungswert np ≈ 16.667 und Varianz npq ≈ 13.889 bzw. Standardabweichung σ ≈ 3.727.
Für die Darstellung einer Binomialverteilung durch eine Normalverteilung sollte die Bedingung n⋅p⋅q ≥ 9 erfüllt sein. In unserem Fall trifft dies zu (n⋅p⋅q = 13.9). Mit nur 50-mal Würfeln wäre diese Bedingung noch nicht erfüllt.
Wir wählen wieder z* = ±1.96. Die Rücktransformation X = μ + σZ ergibt für den 95%-Vertrauensbereich (16.667 ± 1.96⋅3.727), d.h. das Intervall [9.36;23.97]. Mit mehr als 95%-iger Wahrscheinlichkeit (exakt: 96.9%-iger Wahrscheinlichkeit) würfelt man somit in 100 Würfen zwischen 9 und 24 Sechsen.
Schätzung des Erwartungswerts μ der Grundgesamtheit aus dem Mittelwert![]() einer hinreichend grossen Stichprobe (Vertrauensintervall für einen Erwartungswert):
einer hinreichend grossen Stichprobe (Vertrauensintervall für einen Erwartungswert):
Wir können das Beispiel 1 von Kapitel 16 mit den Körpergewichten auch so auffassen:
Wir kennen diesmal den Erwartungswert des Körpergewichts der Grundgesamtheit nicht. Hingegen kennen wir die Werte einer Stichprobe vom Umfang n = 30. Sie ergebe z.B. einen Stichprobenmittelwert![]() = 70.50 kg. Die Standardabweichung σ der Grundgesamtheit sei bekannt und gleich 8 kg (dies ist eine etwas unrealistische Annahme, die wir später nicht mehr benötigen: siehe t-Test).
= 70.50 kg. Die Standardabweichung σ der Grundgesamtheit sei bekannt und gleich 8 kg (dies ist eine etwas unrealistische Annahme, die wir später nicht mehr benötigen: siehe t-Test).
Wir suchen nun ein sogenanntes Vertrauensintervall, das mit 95%-iger Wahrscheinlichkeit den richtigen Erwartungswert μ der Grundgesamtheit überdeckt.
Wir wissen, dass die Stichproben-Mittelwerte normalverteilt sind. Das zugehörige z* für die 95%-Vertrauensgrenze (links und rechts je 2.5% abschneiden) ist z* = ±1.96.
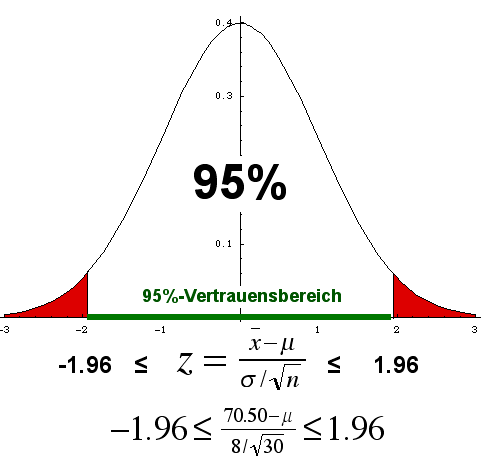
Wir multiplizieren die Ungleichung der Spalte links unten mit σ/√n und erhalten:
-1.96⋅σ/√n ≤ (![]() - μ) ≤ 1.96⋅σ/√n.
- μ) ≤ 1.96⋅σ/√n.
Das bedeutet, dass sich mit 95%-iger Wahrscheinlichkeit das unbekannte μ vom Stichprobenmittelwert ![]() betragsmässig um höchstens 1.96⋅σ/√n unterscheidet, in unserem Fall um
betragsmässig um höchstens 1.96⋅σ/√n unterscheidet, in unserem Fall um
1.96⋅8/√30 kg = 2.86 kg.
Wir können dies auch so ausdrücken:
|
Wir erhalten das Intervall
[70.50kg-2.86kg; 70.50kg+2.86kg] = [67.64 kg; 73.36 kg].
Dieses Intervall überdeckt mit 95%-iger Wahrscheinlichkeit den unbekannten (aber natürlich fix gegebenen!) Erwartungswert μ der Grundgesamtheit.
Hätten wir eine andere Stichprobe gewählt, wäre ein anderer Wert für![]() entstanden. Das Vertrauensintervall wäre gegenüber dem ersten (leicht) verschoben, überdeckte aber immer noch mit 95%-iger Wahrscheinlichkeit den fixen, aber unbekannten Erwartungswert μ.
entstanden. Das Vertrauensintervall wäre gegenüber dem ersten (leicht) verschoben, überdeckte aber immer noch mit 95%-iger Wahrscheinlichkeit den fixen, aber unbekannten Erwartungswert μ.
Falls wir ein 99%-Konfidenzintervall möchten, wählen wir z* = ±2.58. Dieses Intervall wird dann natürlich breiter, da wir ja mehr Sicherheit im Überdecken von μ wollen.
Vorschau auf t-Tests und die t-Test-Verteilung
Die Annahme im eben behandelten Beispiel, dass die Standardabweichung der Grundgesamtheit bekannt sei, ist in der Praxis meist nicht berechtigt. Fast nie kennt man diesen Wert. Es liegt nun nahe, anstelle des unbekannten σ die aus der Stichprobe berechnete empirische Standardabweichung s in die Formel für die Berechnung des Vertrauensintervalls einzusetzen.
Dies würde aber bei kleineren Stichproben zu Schätzfehlern führen. Sealy Gosset entwickelte zu diesem Zweck die sogenannte Student- oder t-Verteilung (da er als Ingenieur einer Bierbrauerei seine dort entwickelte Idee nicht unter seinem Namen veröffentlichen konnte, wählte er das Pseudonym "Student").
Die t-Verteilung ähnelt der Standardnormalverteilung, ist wie diese symmetrisch und eingipflig (glockenförmig) mit Erwartungswert 0. Die t-Verteilung ist aber schmalgipfliger als die Standardnormalverteilung, geht jedoch mit wachsender Zahl der Freiheitsgrade, d.h. mit wachsendem n, in die Standardnormalverteilung über.
Vertrauensintervall mittels t-Verteilung:
Die Zufallsvariable X muss normalverteilt sein. Dann kann das Vertrauensintervall bei unbekanntem σ wie folgt mittels der empirischen Standardabweichung der Stichprobe geschätzt werden (t* stellt die in einer Tabelle nachzuschlagende Konfidenzgrenze dar):
Dabei werden anstelle der z-Werte einer Normalverteilung die (in Tabellen nachschlagbaren) t-Werte einer t-Verteilung benützt. Es ist hier zu beachten, dass je nach Grösse n der Stichprobe die t-Verteilung ändert. Hat die Stichprobe Umfang n, so sagt man, die t-Verteilung habe f = n - 1 "Freiheitsgrade". Für jedes f gibt es eine spezielle t-Verteilung.
In unserem Beispiel oben müsste anstelle von z* = ±1.96 der t-Wert aus der Verteilung mit f = 29 Freiheitsgraden, nämlich t* = ±2.045 (für ein 95%-Vertrauensintervall - links und rechts werden je 2.5% Fläche abgeschnitten) gewählt werden, wenn anstelle des unbekannten σ die Standardabweichung s der Stichprobe verwendet wird.
Schätzung einer Wahrscheinlichkeit p aus der relativen Häufigkeit eines Ereignisses bei n Zufallsexperimenten bzw. einer Stichprobe des Umfangs n (Vertrauensintervall für p)
Sei h : = X / n die relative Häufigkeit eines Ereignisses bei n Zufallsexperimenten.
Wir suchen wiederum ein 95%-Vertrauensintervall (z* = ±1.96), diesmal für das unbekannte p. Ein solches Intervall ist gegeben durch

Für andere Prozentwerte des Vertrauensintervalls ersetze man z* = 1.96 durch die entsprechende, in einer Tabelle nachzuschlagende Zahl.
Bemerkung: Der Summand 1/(2n) vergrössert das Vertrauensintervall ein wenig, um Schätzfehler bei kleinen Stichprobenumfängen n auszugleichen.
Bedingungen an n, damit die Formel links angewendet werden kann: n⋅h > 5 und n⋅(1 - h) > 5. |
Beispiel: Lösung: |
An die Stelle der Prüfgrösse
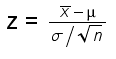
tritt die Prüfgrösse
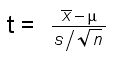 |
d.h. man schätzt die unbekannte Standardabweichung σ durch die bekannte Stichproben-Standardabweichung s.
μ ist z.B. ein Soll-Erwartungswert mit dem der Stichprobenmittelwert ![]() verglichen wird. Die Stichprobenwerte xi müssen normalverteilt sein. Die Zahl f der "Freiheitsgrade" ist im Ein-Stichproben-Test gleich n - 1 (wichtig für's Nachschlagen in der Tabelle).
verglichen wird. Die Stichprobenwerte xi müssen normalverteilt sein. Die Zahl f der "Freiheitsgrade" ist im Ein-Stichproben-Test gleich n - 1 (wichtig für's Nachschlagen in der Tabelle).
Aus langjähriger Erfahrung geht man beim Geburtsgewicht in einer Frauenklinik vom Erwartungswert μ0 = 3500 g aus. Nun will man untersuchen, ob Kinder einer bestimmten Gruppe von Müttern (die z.B. gewissen Risikofaktoren ausgesetzt waren) ein anderes Geburtsgewicht haben.
H0 : Erwartungswert μ der Risikogruppe = Erwartungswert μ0
H1 : Erwartungswert μ der Risikogruppe ≠ Erwartungswert μ0 (zweiseitiger Test)
(Je nach Vorwissen könnte auch einseitig getestet werden.)
Testgrösse: t.
Man misst die Geburtsgewichte einer Stichprobe mit n = 25 aus der Risikogruppe und findet z.B. folgende Werte:
![]() = 3300 g, Standardabweichung s = 400 g.
= 3300 g, Standardabweichung s = 400 g.
Unter Annahme von H0 ergibt sich t = (3300 - 3500) / (400 / √25) = -200/80 = -2.500.
Wir schlagen in einer t-Tabelle nach (f = n - 1 = 24, Niveau 5%, d.h. wir wollen auf jeder Seite der Verteilung 2.5% Fläche abschneiden). Wir finden t* = ±2.064.
Unsere Testgrösse -2.500 befindet sich links von -2.064, also im Ablehnungsbereich. Wir lehnen
somit H0 auf dem 5%-Niveau ab.
Auf dem 1%-Niveau ergäbe sich t* = ±2.797 und wir wären im Annahmebereich von H0. Das Resultat zugunsten von H1 ist signifikant, aber nicht hochsignifikant.
95%-Vertrauensintervall für μ:
-2.064 ≤ (3300 - μ)/80 ≤ 2.064 => |3300 - μ| ≤ 164.8 =>
95%-Vertrauensintervall = [3300-164.8 ; 3300+164.8] = [3135.2 ; 3464.8].
Mit 95%-iger Wahrscheinlichkeit wird der Erwartungswert μ der Risikogruppe von diesem Intervall überdeckt.
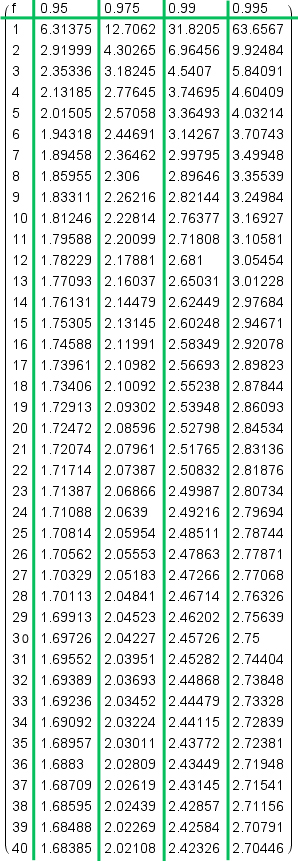
18.2. t-Verteilungs-Tabelle (Werte für einseitige Tests):
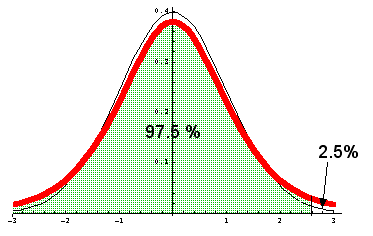
Rot: Dichtefunktion der t-Verteilung für f = 5 ; schwarz zum Vergleich: Dichtefunktion der Normalverteilung. Wollen wir rechts 2.5% abschneiden, ergibt sich aus der Zeile mit f = 5 und der Spalte 0.975 (= 97.5%) der Wert t* = 2.57058.
Vom Bild her mag man denken, dass die beiden Graphen sich nicht gross unterscheiden. Trotzdem sind die t-Werte von den z-Werten für kleinere n recht verschieden. Man bedenke, dass die rote Kurve ganz rechts bis ins Unendliche oberhalb der schwarzen Kurve verläuft. Will man von rechts her 2.5% Fläche unterhalb der roten Kurve abschneiden, muss der Schnitt deutlich weiter rechts erfolgen als bei der schwarzen Kurve. Für n → ∞ geht die t-Verteilung in die Standardnormalverteilung über.
Anleitung:
f = Anzahl Freiheitsgrade
Kopfzeile: Konfidenzwahrscheinlichkeiten = Fläche unter der t-Glockenkurve
von -∞ bis t*.
Tabelleneinträge: Vertrauensgrenzen t* für die entsprechend gewählte Konfidenzwahrscheinlichkeit.
Beispiel:
Einstichproben-Test, n = 25 => f = 24. Wir testen zweiseitig auf dem 5%-Signifikanzniveau und suchen die Vertrauensgrenze t*. Da wir zweiseitig testen, schneiden wir links und rechts je 2.5% Fläche ab. Wir schauen also für die rechte Grenze t* in der Spalte 0.975 (= 97.5%) nach und finden in der Zeile f = 24 den t*-Wert 2.0639. Da die t-Verteilung symmetrisch um den Mittelwert 0 verläuft, ist die linke Konfidenzgrenze gleich -2.0639.
Zwischen diesen beiden Grenzen befinden sich 95% der Fläche unter der Glockenkurve.
Der Test dient dem Vergleich der Mittelwerte zweier unabhängiger Stichproben. Man vergleicht etwa zwei Therapieformen miteinander (Gruppe 1: Therapie 1; Gruppe 2: Therapie 2).
Voraussetzung: Die Daten beider Stichproben müssen normalverteilt sein und dieselbe Varianz haben (die jedoch in der Regel nicht bekannt ist).
Gruppe 1: Grösse n1, Mittelwert ![]() , unbekannter Erwartungswert μ1.
, unbekannter Erwartungswert μ1.
Gruppe 2: Grösse n2, Mittelwert ![]() , unbekannter Erwartungswert μ2.
, unbekannter Erwartungswert μ2.
Getestet wird die Differenz der empirischen Mittelwerte.
Nullhypothese: μ1 - μ2 = 0, d.h. Die Differenz der empirischen Mittelwerte hat Erwartungswert 0 (und ist normalverteilt).
Herleitung der Prüfgrösse:
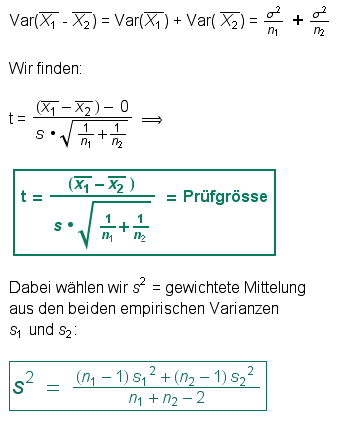
Die Anzahl der Freiheitsgrade ist f = n1 + n2 - 2.
Beispiel 1:
Wir vergleichen die Körpergrössen in cm zwischen Teilgruppe 1 (Herren) und Teilgruppe 2 (Damen) einer bestimmten Personengruppe.
Wir finden z.B. folgende Daten:
n1 = 18, ![]() = 176.5 cm, s1= 7.5
= 176.5 cm, s1= 7.5
n2 = 24, ![]() = 170.0 cm, s2= 7.1
= 170.0 cm, s2= 7.1
f = 40; s2 = (17⋅ 56.25 + 23⋅50.41) / 40 ≈ 52.892 => s ≈ 7.27
t = 6.5 / (7.27 ⋅ √0.3118) ≈ 2.86639 = Prüfgrösse.
Testen wir zweiseitig (auf jeder Seite der t-Dichtefunktion je 2.5% Fläche abschneiden), so finden wir in obiger Tabelle (Zeile f = 40, Spalte 97.5%) den Wert t* = 2.02108.
Unsere Testgrösse befindet sich rechts davon, also im Ablehnungsbereich der Nullhypothese. Sogar die Zahl t* = 2.70446 in Spalte 99.5% führt zur Ablehnung der Nullhypothese, d.h. wir verwerfen sie auch auf dem 1%-Signifikanzniveau. Wir finden also einen hochsignifikanten Unterschied der Mittelwerte der beiden Personengruppen (Männer, Frauen).
Beispiel 2:
Man will die Wirksamkeit einer bestimmten Substanz auf die Konzentrationsfähigkeit einer Person testen. Dazu testen wir in einem Doppelblindversuch je 15 Personen. Gruppe 1 erhält während einer definierten Zeitspanne die Substanz, Gruppe 2 ein Placebo-Produkt. (In einem Doppelblindversuch wissen weder die Probanden noch die Versuchsleiter, wer zur Placebo-Gruppe gehört.) Anschliessend wird ein geeichter Konzentrationstest durchgeführt, dessen Resultat eine "Konzentrationszahl" ist. Wir vergleichen die Mittelwerte dieser Konzentrationszahlen für jede Gruppe separat und finden z.B. folgende Ergebnisse:
n1 = 15, ![]() = 112, s1= 14 (Gruppe, welche die Substanz erhielt).
= 112, s1= 14 (Gruppe, welche die Substanz erhielt).
n2 = 15, ![]() = 100.5, s2= 16 (Placebo-Gruppe).
= 100.5, s2= 16 (Placebo-Gruppe).
f = 28. s2 = (14⋅ 196 + 14 ⋅256) / 28 ≈ 226 => s ≈ 15.033296.
t = 11.5 / (15.033296 ⋅ √0.1333) ≈ 2.09495 = Prüfgrösse.
Wir testen zweiseitig. Die für das 5%-Signifikanz-Niveau nötige Grenzgrösse
t* = 2.04841 (Zeile f = 28) wird von der Prüfgrösse knapp überschritten; wir landen knapp im Ablehnungsbereich der Nullhypothese und finden eine signifikante, jedoch nicht hochsignifikante Abweichung des Konzentrations-Mittelwertes bei der Nichtplacebo-Gruppe.
Ein äquivalenter Test zum Vergleich der Mittelwerte zweier unabhängiger Stichproben ist die einfaktorielle Varianzanalyse mit Zählerfreiheitsgrad 1 basierend auf der Fisher-Verteilung.
Hier werden zwei Gruppen miteinander verglichen, deren Elemente einander paarweise zugeordnet sind (Beobachtungspaare). Beispiel: Vorher-Nachher-Tests, Morgen-, Abendmessungen, usw. Wir betrachten wiederum die Mittelwert-Unterschiede. Die Nullhypothese lautet wie oben: gleiche Erwartungswerte.
Wir bilden für jedes Messpaar (xi , yi ) die Differenz di = xi - yi . Der Mittelwert der
di -Werte ist gleich
![]() .
.
Mittelwert und Varianz der di -Werte sind unbekannt.
Voraussetzung: Die
di -Werte müssen normalverteilt sein.
Wir bestimmen wieder die Stichprobenvarianz s der di -Werte und verwenden die Prüfgrösse der Einstichprobentests unter Voraussetzung der Nullhypothese ("Mittelwert der di -Werte gleich Null"):
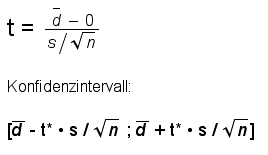 |
s ist dabei die empirische Standardabweichung der di -Werte.
Beispiel:
Nochmals das Beispiel "Einfluss eines Medikaments auf die Konzentrationsleistung":
Test an 6 Personen.
Prä-Test-Werte:
(105, 98, 101, 100, 97, 99).
Post-Test-Werte: (108, 99, 100, 103, 100, 101)
Wir testen aufgrund von Vorwissen einseitig und verwenden als Differenzen die Werte "Post-Test minus Prä-Test".
Differenzen: (3, 1, -1, 3, 3, 2)
Mittelwert: 1.833
Standardabweichung: 1.602
t = 1.833 / (1.602/√6) ≈ 2.803.
t* in Zeile für f = 5 nachschlagen in Spalte 95%: t* = 2.015.
Die Testgrösse befindet sich im Ablehnungsbereich. Auf dem 5%-Niveau verwerfen wir die Nullhypothese "kein Einfluss auf Konzentrationsleistung". Auch auf dem 2.5%-Niveau ergäbe sich noch eine Verwerfung der Nullhypothese (t* = 2.571).
Auf dem 1%-Niveau jedoch ist t* = 3.365 und wir befinden uns im Annahmebereich der Nullhypothese.
Die Alternativhypothese ("Einfluss") wird signifikant, jedoch nicht hochsignifikant gestützt.
Bemerkung: Die Statistik liefert aufgrund der erhobenen Daten Resultate, die zur Annahme oder Verwerfung der Nullhypothese führen. Ob das Test-Design sinnvoll ist oder ob sich allenfalls systematische Fehler einschleichen, "merkt" die statistische Rechnung nicht. Im vorliegenden Fall könnte das bessere Abschneiden im Post-Test auch damit zu tun haben, dass die Probanden beim zweiten Mal mit einem solchen Test vertrauter sind als beim ersten Mal. Die verbesserte Leistung ginge dann ev. nicht aufs Konto des verabreichten Mittels. Die Planerinnen und Planer dieses Experiments müssen sich also vorher überlegen, wie sie einen solchen Störfaktor "austricksen" könnten.
Allenfalls betrachtet man ein Histogramm.
Falls Mittelwert und Median stark auseinanderfallen, ist die Normalverteilung nicht gegeben.
Bei kleinen Stichprobenumfängen ist auf den Wilcoxon-Test auszuweichen.
t-Test für zwei unverbundene Stichproben: n ≥ 10, bei nichtsymmetrischen Verteilungen besser ≥ 20 und für beide Stichproben ähnlich gross. Beide Zufallsgrössen ähnlich verteilt.
Diese Tests haben weniger enge Voraussetzungen als die t-Tests, da sie keine bestimmte Verteilung der Daten voraussetzen. Die Prüfgrösse wird aus den Rangzahlen der Messwerte berechnet. Man kann diese Tests deshalb sogar für ordinal skalierte Daten verwenden, da es nur auf deren Rangfolge ankommt.
Der Wilcoxon-Test für eine Stichprobe vergleicht den Median einer Stichprobe mit einem Soll-Median.
Nullhypothese: Median der Grundgesamtheit, aus der die Stichprobe stammt ist gleich gross wie der vorgegebene Soll-Median.
Vorgehen:
- Berechnung der Differenzen zwischen Stichprobenwerten und Sollwert. Ist die Differenz 0, wird der betreffende Stichprobenwert nicht beachtet.
- Ordnen der Absolutbeträge der Differenzen aufsteigend von klein nach gross -> Jede Differenz erhält so eine Ranzahl von 1 bis n. (Bei Gleichheit der Differenzen mittelt man die Rangzahlen: Sind etwa an 3., 4., 5. und 6. Stelle vier gleiche Differenzen, gibt man jeder die Rangzahl 4.5.)
- Die Rangzahlen der negativen Differenzen werden addiert , ebenso die Rangzahlen der positiven Differenzen. Die kleinere dieser beiden Rangsummen ist die Testgrösse R.
- Die Verwerfungsgrenzen schlägt man in der entsprechenden Tabelle nach.
Bemerkungen:
Für n > 25 ist die Testgrösse unter der Nullhypothese etwa normalverteilt mit Erwartungswert n (n + 1) / 4 und Varianz n (n + 1)(2n + 1) / 24.
R = 0 bedeutet maximale Abweichung vom Soll-Median. Ist jedoch die Nullhypothese gültig, erwartet man gleiche Rangsummen der Grösse n (n + 1) / 4. Kleine Prüfgrössen führen also zur Ablehnung der Nullhypothese, grosse zur Beibehaltung.
Der Test setzt keine Normalverteilung, aber eine symmetrische Verteilung voraus.
Differenzen mit grossen Rängen (also hohe Abweichungen vom Sollwert) zählen bei diesem Test stärker als Differenzen mit kleinen Rängen.
Beispiel:
Man wägt die 500g-Brote einer Firma. Nullhypothese: Die effektiven Brotmassen entsprechen dem Sollwert 500g.
Resultate:
Masse: 495 509 505 498 499 510 520 490 500 502 497 501 500 497 501 501
Differenz: -5 9 5 -2 -1 10 20 -10 0 2 -3 1 0 -3 1 1
Rang: 9.5 11 9.5 5.5 2.5 12.5 14 12.5 - 5.5 7.5 2.5 - 7.5 2.5 2.5
Rangsumme R(+) = 60, Rangsumme R(-) = 45. Probe: 60+45 = 14⋅15/2=105.
Testgrösse = 45. n = 14 (2 Messungen wurden eliminiert, da exakt 500 g).
Nachschlagen in Tabelle unten (n = 14, 5%-Niveau) ergibt die Verwerfungsgrenze 21.
Da die Testgrösse 45 grösser ist als 21, wird die Nullhypothese beibehalten.
Kritische Grenzen für den Wilcoxon-Test
Tabelle rechts: Kritische Grenzen für zweiseitige Tests auf dem 5%-Niveau oder für einseitige Tests auf dem 2.5%-Niveau.
Die Nullhypothese wird abgelehnt, wenn die Prüfgrösse R ≤ dem kritischen Wert gemäss Tabelle rechts ist.
| n | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| R2.5% | 0 | 2 | 3 | 5 | 8 | 10 | 13 | 17 | 21 | 25 | 29 | 34 | 40 |
| n | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| R2.5% | 46 | 52 | 58 | 65 | 73 | 81 | 89 | 98 | 107 | 116 | 126 | 137 |
Analog zum t-Test unter 18.3, wenn man keine Normalverteilung annehmen kann. Es werden die beiden Mediane verglichen. Die Zufallsvariablen aus den beiden zu vergleichenden Bereichen sollen ungefähr die gleiche Verteilungsform haben, müssen aber nicht symmetrisch verteilt sein.
Seien n1 und n2 die Umfänge der beiden zu vergleichenden Stichproben.
Nullhypothese: "Erwartungswerte beider Mediane gleich."
Die Werte beider Stichproben werden in eine gemeinsame, aufsteigende Reihe gebracht und mit Rangnummern versehen. Man addiert dann die Ränge von Stichprobe 1 => R1 und von Stichprobe 2 => R2.
Nun berechnet man folgende Grössen:
Gleichbedeutend ist:
|
Ist U ≤ dem kritischen Wert in der entsprechenden Tabelle, wird die Nullhypothese abgelehnt.
Bemerkungen:
Für Stichproben mit mehr als 10 Werten pro Stichprobe ist U unter der Nullhypothese annähernd normalverteilt mit Erwartungswert n1 (n1 + n2 + 1) / 2 und Varianz n1n2 /6.
n1 ist dabei der kleinere Stichprobenumfang. Kleine Prüfgrösse (gegen 0) bedeutet einen grossen Unterschied zwischen den Stichproben, d.h. Tendenz zur Alternativhypothese.
Man vermeide gleiche Ränge zwischen den beiden Stichproben (genauer messen).
Mittels dieses Tests können auch ordinal skalierte Merkmale geprüft werden.
Beispiel: Vergleich zwischen Männern und Frauen bezüglich Fragebogen-Skalen zu persönlichen Einstellungen etwa der Art:
-3 -2 -1 0 +1 +2 +3
völlige Ablehnung völlige Zustimmung
Rangsummentests führen eher zur Beibehaltung der Nullhypothese als t-Tests.
Eine Tabelle mit den kritischen Werten findet sich leicht im Internet.
Hier ein Beispiel.
Hier ein Link zu einer Seite, welche Berechnungen ermöglicht.
Beispiel (fiktiv):
Wirkung eines Medikaments auf die Konzentration (siehe 18.3., Beispiel 2). Doppelblindversuch. Gruppe 1: Medikamentengruppe, Gruppe 2: Placebogruppe.
Nehmen wir an, der Versuch ergäbe die in der Tabelle rechts aufgeführten "Konzentrationszahlen" eines Konzentrationstests am Schluss der Versuchsphase:
Testgrösse U = 57.
Kritische Grenze (Tabelle mit n1 = n2 = 15): 64.
Es ist 57 < 64 => Die Nullhypothese ("Gleiche Erwartungswerte bei beiden Gruppen") wird somit auf dem 5%-Niveau verworfen.
Abgesehen vom rein statistischen Zahlenergebnis liesse sich (falls ein solches Ergebnis einträte - unser Beispiel ist ja rein fiktiv) überlegen, warum die Standardabweichung von Gruppe 1 kleiner ist als diejenige von Gruppe 2. Hier eröffnen sich weitere Fragen: Wirkt das Mittel auf alle Personen gleichermassen; wären ev. geschlechtsspezifische Unterschiede in der Wirkung möglich, usw.? Es zeigt sich einmal mehr, dass statistische Ergebnisse nicht einfach "Schlussresultate" sind, sondern zu weiteren Fragen und Untersuchungen anregen können.
| Medikamentengruppe | Rang | Placebogruppe | Rang |
| 103 | 12 | 111 | 15 |
| 116 | 21 | 114 | 18 |
| 128 | 29.5 | 112 | 16 |
| 95 | 10 | 80 | 2 |
| 94 | 9 | 90 | 7 |
| 115 | 20 | 96 | 11 |
| 125 | 27 | 107 | 13 |
| 114 | 18 | 80 | 2 |
| 118 | 22 | 119 | 23 |
| 91 | 8 | 85 | 5 |
| 125 | 27 | 80 | 2 |
| 120 | 24.5 | 110 | 14 |
| 128 | 29.5 | 114 | 18 |
| 88 | 6 | 125 | 27 |
| 120 | 24.5 | 84 | 4 |
| Mittelwert 112.0 | Mittelwert 100.5 | ||
| Standardabw. 14.0 | Standardabw. 16.0 | ||
| R1 | 288 | R2 | 177 |
| U1 | 57 | U2 | 168 |


Mit Chi2-Tests werden Häufigkeitsunterschiede analysiert. Beispiele:
- Erfolgsvergleich zweier Therapiegruppen (Vierfelder-Test)
- Vergleich der Unabhängigkeit zweier Merkmale (Bsp: Gibt es einen Zusammenhang zwischen Berufszielen und Geschlecht?): Vierfelder-Test.
- Vergleich der relativen Häufigkeiten einer Stichprobe mit theoretischen Wahrscheinlichkeiten
Grundidee des Chi2-Tests:
Die beobachteten Häufigkeiten werden verglichen mit den theoretisch bei Gültigkeit der Nullhypothese zu erwartenden Häufigkeiten (den Wahrscheinlichkeiten).
Man berechnet die Quotienten
(beobachtete Häufigkeit - erwartete Häufigkeit)2 / erwartete Häufigkeit
und addiert sie. Das ergibt die Testgrösse (vgl. Bsp. links unten).
Beispiel: Ist der Würfel "gerecht"?
Ein Würfel, der mir von Auge etwas "suspekt" erscheint, soll getestet werden. Ich werfe ihn 120-mal und notiere die erwürfelten Augenzahlen. Der Versuch ergibt folgende Ergebnisse:
| Augenzahl | beobachtete Augenzahl B | theoretisch zu erwartende Augenzahl E |
(B - E)2 / E |
| 1 | 21 | 20 | 0.05 |
| 2 | 27 | 20 | 2.45 |
| 3 | 11 | 20 | 4.05 |
| 4 | 13 | 20 | 2.45 |
| 5 | 24 | 20 | 0.80 |
| 6 | 24 | 20 | 0.80 |
| Summe | 120 | 120 | 10.60 |
Die Anzahl f der Freiheitsgrade ist gleich der Anzahl Beobachtungsklassen minus 1, also in unserem Beispiel gleich 5.
Die Prüfgrösse ist "Chi2-verteilt" mit f "Freiheitsgraden".
Eine Tabelle liefert zum 5%-Signifikanzniveau den kritischen Wert 11.070. Unsere Testgrösse ist kleiner, liegt also noch im Annahmebereich der Nullhypothese. Wir können die Nullhypothese "gerechter Würfel" nicht verwerfen.
Bemerkung: Im Chi2-Test sollen alle zu erwartenden Häufigkeiten ≥ 5 sein. Zudem darf keine der beobachteten Häufigkeiten gleich 0 sein.
Grafik zur Chi2-Verteilung: http://de.wikipedia.org/wiki/Chi-Quadrat-Verteilung
Tabelle zur Chi2-Verteilung: http://de.wikipedia.org/wiki/Chi-Quadrat-Test#Tabelle_der_Quantile_der_Chi-Quadrat-Verteilung
Beispiel: Ist dieser "Wurf" mit 36 Würfeln arrangiert oder ist es plausibel, dass er "als Wurf" entstanden ist?
Nullhypothese: "Als Wurf entstanden."

| Augenzahl | beobachtete Augenzahl B | theoretisch zu erwartende Augenzahl E |
(B - E)2 / E |
| 1 | 7 | 6 | 1/6 |
| 2 | 4 | 6 | 4/6 |
| 3 | 6 | 6 | 0 |
| 4 | 5 | 6 | 1/6 |
| 5 | 11 | 6 | 25/6 |
| 6 | 3 | 6 | 9/6 |
| Summe | 36 | 36 | 40/6 ≈ 6.667 |
6.667 < 11.070: Die Nullhypothese wird nicht verworfen.
Der Vierfelder-Unabhängigkeits-Test
In diesem Test ist f = 1.
Beispiel aus Ineichen, Robert, Elementare Beispiele zum Testen statistischer Hypothesen, Orell Füssli, Zürich, 1978, vergriffen, p.75 ff.
Ist der Anteil Verkehrsunfälle mit tödlichem Ausgang am Wochenende derselbe wie unter der Woche (Nullhypothese)? Die Nullhypothese besagt also, dass die Merkmale "Wochenende" und "Verkehrsunfälle mit tödlichem Ausgang" voneinander unabhängig sind.
A = Anteil Verkehrsunfälle mit tödlichem Ausgang
A' = Anteil Verkehrsunfälle ohne tödlichen Ausgang
B = Wochenende
B' = Montag - Freitag
Man findet z.B. folgende Zahlen (Vierfeldertafel):
| A | A' | Total | |
| B | 2808 | 45708 | 48516 (35.7%) |
| B' | 4680 | 82680 | 87360 (64.3%) |
| Total | 7488 (5.51%) | 128388 (94.49%) | 135876 = n (100%) |
Wir nehmen diese Zahlen als Schätzwerte für die Unfall-Wahrscheinlichkeiten:
p(A) = 0.05510907, p(A') = 0.94489093, p(B) = 0.35706085, p(B') = 0.64293915
Unter der Nullhypothese ("Unabhängigkeit") muss gelten (Multiplikationsgesetz für unabhängige Ereignisse):
P(B UND A) = P(B)⋅P(A) = 0.01967729
P(B UND A') = P(B)⋅P(A') = 0.33738356
P(B' UND A) = P(B')⋅P(A) = 0.03543178
P(B' UND A')=P(B')⋅P(A') = 0.60750737
Multiplizieren wir diese theoretischen Wahrscheinlichkeiten mit n, der Gesamtzahl der Unfälle, erhalten wir die unter der Nullhypothese zu erwartenden Zahlen:
Zu erwartenden Zahlen:
| A | A' | |
| B | 2674 | 45842 |
| B' | 4814 | 82546 |
Nun bilden wir wieder für jedes der vier Felder die Werte (B - E)2 / E:
| A | A' | |
| B | 6.7488 | 0.3936 |
| B' | 3.7480 | 0.2186 |
Die Summe ergibt die Testgrösse 11.109. Die Gefahr besteht, beim Berechnen beträchtliche Rundungsfehler zu begehen. Praktischer wäre deshalb eine Formel für die Testgrösse direkt aus den Angaben der ursprünglichen Tabelle.
Ohne Beweis geben wir an, wie wir die Testgrösse direkt aus der ursprünglichen Vierfeldertafel berechnen können:
Sei
| A | A' | |
| B | a | b |
| B' | c | d |
die ursprüngliche Vierfeldertafel. Dann berechnet sich die Testgrösse zu
|
Mit unseren Zahlen ergibt sich die Testgrösse ohne grössere Rundungsfehler zu 11.1090211.
Die Zahl der Freiheitsgrade ist im Vierfeldertest gleich 1. Wir finden als kritischen Wert in einer Tabelle für f = 1 die Zahl 3.841 (5%-Niveau). Für das 1%-Niveau finden wir den kritischen Wert 6.635. Unser Wert 11.109 liegt also im Verwerfungsbereich der Nullhypothese. Das Wochenende zeigt mit den Zahlen unseres Beispiels hochsignifikant mehr tödliche Unfälle als die übrige Woche.
Beim Vierfeldertest sollte n≥ 30 sein. Wieder sollten die erwarteten Häufigkeiten ≥ 5 sein.
Weitere Testmöglichkeiten:
- Männer - Frauen / RaucherInnen - NichtraucherInnen
- Behandlungsmethode 1 - Behandlungsmethode 2 / Erfolg gut - Erfolg schlecht
- Knaben - Mädchen / Klausurergebnis unter gemeinsamem Median - Klausurergebnis über gemeinsamem Median (Mediantest)
- Männer - Frauen / Test bestanden - Test nicht bestanden
Nullhypothese des F-Tests:
Die beiden zu vergleichenden Stichproben entstammen aus Grundgesamtheiten mit gleicher Varianz:
(σ1)2 = (σ2)2.
Prüfgrösse: F = (s1)2 : (s2)2.
Voraussetzung: Stichproben unabhängig, Merkmal in beiden Populationen normalverteilt.
F-Verteilung mit
n1 - 1 Zähler- und n2 - 1 Nennerfreiheitsgraden.
Achtung: Bei einseitigem Test: Diejenige Stichprobenvarianz in den Zähler nehmen, welche nach der Alternativhypothese
H1 die grössere sein müsste.
Zweiseitiger Test: Grössere der beiden Stichprobenvarianzen in den Zähler; dann muss man am linken Rand der Verteilung nichts beachten und am rechten Rand α/2 abschneiden.
Beispiel (nach Bortz / Schuster):
Leserschaft Zeitung A; Leserschaft Zeitung B. Nullhypothese: Beide Gruppen gleich homogenes Meinungsspektrum (operationalisiert als Meinungsindex aus einem Fragebogen).
Test zweiseitig, α = 0.10.
Fragebogen: 121 Personen aus Leserschaft A und 101 Personen aus Leserschaft B. Daraus abgeleitet ein Meinungsindex; Voraussetzung: normalverteilt.
Resultate:
sA2 = 80, sB2 = 95. Grössere Varianz in den Zähler: 95 : 80 = 1.19.
F-Tabelle; rechts 5% abschneiden (Hälfte von 0.10). Kritischer Wert 1.37. (Zählerfreiheitsgrade 100, Nennerfreiheitsgrade 120.)
1.19 liegt im Annahmebereich der Nullhypothese: Beide Leserschaften unterscheiden sich im Einstellungsspektrum nicht signifikant.