Verfahren der Substitution

Training Textgleichungen mit zwei Unbekannten, 12 Aufgaben am Computer zu lösen

Textaufgaben mit 2 Unbekannten

Gewinnschwelle (break-even) berechnen, 1.Teil

Gewinnschwelle (break-even) berechnen, 2.Teil

Kosten-, Erlös- und Gewinnfunktion berechnen

Kosten-, Erlös- und Gewinnfunktion, Begriffe

Kostenfunktion, Fixkosten, Laufkosten

Wie lauten die Funktionsgleichungen?

Anwendung: Netzwerke und lineare Systeme

Wozu Gleichungssysteme? - Beispiel: Computertomografie

Wozu braucht man Gleichungssysteme? Unsere ganze Technik beruht darauf, dass Computer riesige Gleichungssysteme lösen (mit bis zu 1 Mio. Unbekannten), so etwa in Gebieten wie Navigation und Handytechnik,  Elektronik, Page-Ranking von Google, Verkehrssteuerung, Computertomographie und Krebstherapie.

Regionale Hyperthermie
So wird z.B. an der Berliner Charité oder an der Strahlenklinik der Uni Erlangen erforscht, wie mit regionaler Wärmebestrahlung Tumore, etwa an Enddarm, Gebärmutter, Prostata oder Blase, verkleinert werden können ("Regionale Hyperthermie").
Durch eine solche Verkleinerung werden die Operations-Chancen erhöht.
Antennen erzeugen Radiowellen von etwa 100 MHz. Die Kunst besteht nun darin, diese Antennen und die Strahlung so einzustellen, dass die Temperatur im Tumor möglichst hoch wird, im gesunden Gewebe aber keine Hot-Spots entstehen. Weitere Probleme: Die Wellenlänge verändert sich im Körper durch Wasser- und Fettgehalt der Gewebe, durch Muskeln, Knochen und Organe. Die zugeführte Wärme muss zudem über die Blutbahnen wieder abgeführt werden.
Der Computer erstellt zunächst einen "virtuellen Patienten", der für jeden wirklichen Krebspatienten eigens berechnet wird. Dazu werden 50 - 60 CT-Bilder benötigt.

Bildquelle:http://www.strahlenklinik.uk-erlangen.de/e138/e922/e982/e1001/index_ger.html

Dann wird die Therapie am virtuellen Patienten simuliert. Daraus ergibt sich dann die optimale Einstellung der Strahlung, die schliesslich für den wirklichen Patienten übernommen wird. Zudem muss für den Arzt alles visualisiert werden.
Für die Simulation der Therapie am virtuellen Patienten müssen Gleichungssysteme mit 100'000 bis 1'000'000 Unbekannten gelöst werden. Die Berechnung der Wärmeausbreitung im Körper erfordert wiederum Gleichungs-systeme mit etwa 100'000 Unbekannten.

Computertomografie und Gleichungssysteme
Godfrey Newbold Hounsfield beschrieb 1972 das Prinzip der Computertomographie als erster und erhielt dafür 1979 den Nobelpreis der Medizin. 1987 gelang es Karl-Heinz Höhne, dreidimensionale Rekonstruktionen aus zweidimensionalen CT- und NMR-Schnittbildern zu generieren.

Wie kann man sich das Visualisieren einer tomografischen Messung vorstellen?
Eine kleine Schichtfläche des Körpers wird aus verschiedenen Richtungen bestrahlt. Die Strahlen treten in die Zellen ein, ein Teil der Energie wird in diesen absorbiert, ein Teil verlässt die Zelle wieder. Die reduzierte Ausgangsstrahlung wird gemessen. Wir kann daraus nun ein Bild des Körperinneren konstruiert werden?

Wir betrachten den folgenden schematisierten Körperausschnitt.

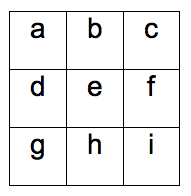
Jedes Quadrätchen kann als kleiner Komplex von Körperzellen eines bestimmten Typs interpretiert werden (Haut-, Knochen-, Leberzellen, usw.). Jedem Quadrätchen ordnen wir eine Zahl a, b, c, d, e, f, g, h, i zu, die sagt, wie stark dieser Komplex die Strahlung absorbiert (CT-Zahl; Hounsfield-Unit). Eine hohe Zahl bedeutet, dass die eintretende Strahlung nur noch sehr geschwächt austritt, dass also ein grosser Teil der Energie absorbiert wird, eine kleine Zahl bedeutet wenig Absorption. Knochenzellen absorbieren stärker als etwa Hautzellen.

Nun bestrahlen wir die Schicht aus verschiedenen Richtungen. Die Eintritts-Intensität der Strahlung (genauer: der Logarithmus davon) sei z.B. 30. Die Austritts-Intensitäten (d.h. wieder deren Logarithmen) sind hier als Beispiel angegeben:

Teilbild a) Einstrahlwinkel 0°. Streckenlänge pro Quadrätchen: 1.
Teilbild b) Einstrahlwinkel 24.6°. Streckenlänge pro Quadrätchen: 1.1.
Teilbild c) Einstrahlwinkel 45°. Streckenlänge pro Quadrätchen: 1.4.

Beispiel: Teilbild a), oberster Pfeil:
Eintrittszahl 30, Austrittszahl 12 =>  Absorptionszahl 18 = a + b + c.
Auf diese Weise erhalten wir für jeden gezeichneten Pfeil eine Gleichung:

a + b + c = 18
d + e + f = 14
g + h + i = 18

1.1d + 1.1b + 1.1c = 18.7
1.1g + 1.1e + 1.1f = 16.5
1.1h + 1.1i  = 13.2

1.4d + 1.4b = 16.8
1.4g + 1.4e + 1.4c = 18.2
1.4h + 1.4f = 19.6

In der Praxis braucht man mehr Gleichungen als Unbekannte, da einige Gleichungen voneinander abhängig sein können.

Gemäss diesen Absorptionszahlen können wir nun die Felder mit Graustufenwerten versehen: Je höher die Absorptionszahl, desto dunkler die Färbung:

Auf diese Art entsteht ein Bild der verschiedenen Gewebezellen, d.h. ein Abbild des Körperinneren.

In Wirklichkeit werden Gleichungssysteme mit ca. 500'000 Unbekannten berechnet. Dazu mussten spezielle Näherungsmethoden für die Auflösung entwickelt werden, da die Anwendung der klassischen Methode zur Lösung von Gleichungssystemen pro Schichtbild eine Rechenzeit von etwa 1 Monat benötigen würde